
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Парольные системы идентификации и аутентификации пользователейСодержание книги
Поиск на нашем сайте
Парольные системы идентификации/аутентификации является одними из основных и наиболее распространенных в СЗИ методов пользовательской аутентификации. В данном случае информацией, аутентифицирующей пользователя, является некоторый секретный пароль, известный только легальному пользователю. Совокупность идентификатора и пароля пользователя называется его учетной записью. База данных пользователей парольной системы содержит учетные записи всех ее пользователей. Парольные системы являются зачастую «передним краем обороны» всей системы безопасности. Отдельные ее элементы могут быть расположены в местах, открытых для доступа потенциальному злоумышленнику (в том числе и база данных учетных записей пользователей). В связи с этим, парольные системы становятся одним из наиболее привлекательных для злоумышленника объектов атаки. Основными типами угроз безопасности парольных систем являются следующие. 1. Перебор паролей в интерактивном режиме. 2. Подсмотр пароля. 3. Преднамеренная передача пароля его владельцем другому лицу. 4. Кража базы данных учетных записей с дальнейшим ее анализом, подбором пароля. 5. Перехват вводимого пароля путем внедрения в КС программных закладок (клавиатурных шпионов); перехват пароля, передаваемого по сети. 6. Социальная инженерия. Многие недостатки парольных систем связаны с наличием человеческого фактора, который проявляется в том, что пользователь, зачастую, стремится выбрать пароль, который легко запомнить (а значит и подобрать), записать сложно запоминаемый пароль, ввести пароль так, что его могут увидеть посторонние, передать пароль другому лицу намеренно или под влиянием заблуждения. Для уменьшения деструктивного влияния человеческого фактора необходимо реализовать ряд требований к выбору и использованию паролей. 1. Задание минимальной длины пароля для затруднения подбора пароля злоумышленником «в лоб» (полный перебор, brute-forcing) и подсмотра. 2. Использование в пароле различных групп символов для усложнения подбора злоумышленником пароля «в лоб». 3. Проверка и отбраковка пароля по словарю для затруднения подбора пароля злоумышленником с использованием словарей. 4. Установление максимального срока действия пароля для затруднения подбора пароля злоумышленником «в лоб», в том числе и в режиме «off-line» при взломе предварительно похищенной базы данных учетных записей пользователей. 5. Применение эвристического алгоритма, бракующего «плохие» пароли для усложнения подбора пароля злоумышленником «по словарю» или с использованием эвристического алгоритма. 6. Ограничение числа попыток ввода пароля для предотвращения интерактивного подбора пароля злоумышленником. 7. Использование задержки при вводе неправильного пароля для предотвращения интерактивного подбора пароля злоумышленником. 8. Поддержка режима принудительной смены пароля пользователя для эффективности реализации требования, ограничивающего максимальный срок действия пароля. 9. Запрет на выбор пароля самим пользователем и автоматическая генерация паролей для затруднения использования злоумышленником эвристического алгоритма подбора паролей. Количественная оценка стойкости парольных систем может быть выполнена с помощью следующего подхода [2]. Пусть A – мощность алфавита паролей (количество символов, которые могут быть использованы при составлении пароля). Например, если при составлении пароля могут быть использованы только малые английские буквы, то A =26. L – длина пароля.
V – скорость перебора паролей злоумышленником. T – максимальный срок действия пароля. Тогда, вероятность P подбора пароля злоумышленником в течении срока его действия Т определяется по следующей формуле.
Эту формулу можно обратить для решения следующей задачи: ЗАДАЧА. Определить минимальные мощность алфавита паролей A и длину паролей L, обеспечивающих вероятность подбора пароля злоумышленником не более заданной P, при скорости подбора паролей V, максимальном сроке действия пароля T. Данная задача имеет неоднозначное решение. При исходных данных V,T,P однозначно можно определить лишь нижнюю границу S* числа всевозможных паролей. Целочисленное значение нижней границы вычисляется по формуле
где После нахождения нижней границы S* необходимо выбрать такие A и L, чтобы выполнялось неравенство (3.2).
При выборе S, удовлетворяющего неравенству (3.2), вероятность подбора пароля злоумышленником (при заданных V и T) будет меньше или равна P. При вычислениях по формулам (3.1) и (3.2), величины должны быть приведены к одной размерности. Пример 3.1 Исходные данные – P =10-6, T =7 дней = 1 неделя, V =10 паролей / минуту = 10*60*24*7=100800 паролей в неделю. Тогда, Условию
Элементы теории чисел Модулярная арифметика Пусть m – целое число. Тогда при делении любых целых чисел на m возможно получение ровно m остатков – 0,1,2,…,m-1. Целые числа a и b называют сравнимыми по модулю m, если их разность a-b делится без остатка на m, или, что то же самое, остатки, получаемые при делении чисел a и b на m, равны между собой. В этом случае число b называют вычетом числа a по модулю m. Если a сравнимо с b по модулю m, то это записывают как Пример 4.1 Целые числа 17 и 12 сравнимы между собой по модулю 5, то есть Существует бесконечное количество чисел, сравнимых с числом a по модулю m, но только одно из них расположено в диапазоне от 0 до m-1. Обычно, для целого числа a>0 предпочитают использовать вычеты Модулярная арифметика аналогична во многом обычной арифметике: она коммутативна, ассоциативна и дистрибутивна. Целые числа по модулю m с использованием операций сложения и умножения образуют коммутативное кольцо при соблюдении законов ассоциативности, коммутативности и дистрибутивности. Основные свойства сравнений: 1. Рефлексивность: 2. Симметричность: 3. Транзитивность: 4. Если 5. Если 6. Если 7. Если 8. Если 9. Если При выполнении арифметических операций по модулю, можно либо сначала приводить операнды по модулю m, а затем выполнять операции, либо сначала выполнять операции, а затем приводить результат по модулю m. В криптографии используется множество вычислений по модулю m, так как с вычислениями по модулю удобнее работать в связи с ограничением диапазона всех промежуточных величин и результата. Кроме того, задачи типа вычисления дискретных логарифмов трудны в вычислительном плане. Для модуля m длиной k бит промежуточные результаты любого сложения, вычитания или умножения будут не длиннее 2k бит. Поэтому такую операцию, как возведение в степень в модулярной арифметике можно выполнить без генерации очень больших промежуточных результатов. Возведение числа a в степень x по модулю m, то есть нахождение Пример 4.2 Пусть, например, требуется вычислить
Например,
Вычисление Пример 4.3 Пусть x=25(10)=11001(2), тогда 25=24+23+20. Тогда
Поскольку многие алгоритмы шифрования основаны на возведении в степень больших чисел в большие степени по большому модулю, целесообразно использовать рассмотренные выше алгоритмы быстрого возведения в степень.
Простые числа и их свойства Натуральное число n >1 называется простым, если оно имеет в точности два различных натуральных делителя – 1 и n, в противном случае n называется составным. Пример 4.4 Числа 2,3,7 являются простыми. Числа 4,6,8 – составными, так как их делителем является число 2. Свойства простых чисел: 1. Если p1 и p2 – простые и 2. Пусть p – простое число, а n – натуральное, тогда n делится на p или наибольший общий делитель чисел n и p равен 1. 3. Если 4. Если Известна следующая теорема: Теорема 4.1. Любое натуральное число n >1 либо просто, либо раскладывается в произведение простых чисел и притом единственным образом с точностью до порядка следования сомножителей: Задача представления числа n в канонической форме называется задачей факторизации числа n. Существенный с точки зрения криптографии факт состоит в том, что в арифметике не известно никакого эффективного алгоритма факторизации числа n. Никаких эффективных методов неизвестно даже в таком простом случае, когда необходимо найти два простых числа p и q, таких, что Известен ряд подходов, позволяющих выполнить проверку простоты целого числа n – решето Эратосфена, критерий Вильсона, тестирование на основе малой теоремы Ферма, тест Соловея-Штрассена, тест Рабина-Миллера и др. Наибольшим общим делителем целых чисел a и b, обозначаемым как НОД (a, b) или просто (a, b), - это наибольшее целое, делящее одновременно числа a и b. Если (a, b)=1, то a и b называют взаимно простыми.
Числовые функции В теории чисел и в криптографии большое значение имеют следующие числовые функции [22].
Пусть канонической формой числа n является
Пример 4.5 Для числа n =720 найдем Представим число 720 в канонической форме - Тогда
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.139.70.69 (0.007 с.) |

 - число всевозможных паролей длины L, которые можно составить из символов алфавита A.
- число всевозможных паролей длины L, которые можно составить из символов алфавита A.
 (3.1)
(3.1) - целая часть числа, взятая с округлением вверх.
- целая часть числа, взятая с округлением вверх. (3.2.)
(3.2.) .
. удовлетворяют, например, такие пары величин A и L, как A =26, L =8 (пароль состоит из 8 малых символов английского алфавита), A =36, L =6 (пароль состоит из 6 символов, среди которых могут быть малые латинские буквы и цифры).
удовлетворяют, например, такие пары величин A и L, как A =26, L =8 (пароль состоит из 8 малых символов английского алфавита), A =36, L =6 (пароль состоит из 6 символов, среди которых могут быть малые латинские буквы и цифры).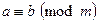 .
.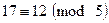 , кроме этого
, кроме этого  .
.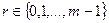 . Набор целых чисел от 0 до (m-1) называют полным набором вычетов по модулю m.
. Набор целых чисел от 0 до (m-1) называют полным набором вычетов по модулю m.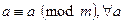 .
. .
. .
. - произвольные целое число, то
- произвольные целое число, то  .
. , то
, то  , то
, то  .
. , то
, то  .
. , то
, то  .
. .
. можно легко выполнить как ряд умножений. Особенно легко возводить в степень по модулю, если
можно легко выполнить как ряд умножений. Особенно легко возводить в степень по модулю, если  - степень двойки.
- степень двойки.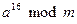 . В этом случае не следует выполнять серию умножений и одно приведение по модулю большого числа. Вместо этого выполняют три малых умножения и три малых приведения по модулю.
. В этом случае не следует выполнять серию умножений и одно приведение по модулю большого числа. Вместо этого выполняют три малых умножения и три малых приведения по модулю.

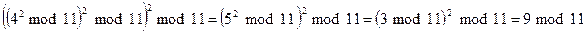

 .
. , то p1 не делится на p2.
, то p1 не делится на p2. делится на простое число
делится на простое число  , то m делится на p или n делится на p.
, то m делится на p или n делится на p.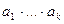 делится на простое число
делится на простое число  , которое делится на
, которое делится на  , где
, где  . Данное разложение называется канонической формой числа n.
. Данное разложение называется канонической формой числа n. .
. - определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая:
- определяет количество простых чисел от 2 до n. Точной формулы для вычисления данной функции не известно. Грубой оценкой данной функции является следующая:  .
. - определяет количество всех делителей числа n.
- определяет количество всех делителей числа n.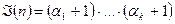 .
. - определяет сумму всех делителей числа n,
- определяет сумму всех делителей числа n, 
 - функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,
- функция Эйлера, определяет количество чисел меньших n и взаимнопростых с n,
 .
.





