Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Шифрование методом гаммированияСодержание книги
Похожие статьи вашей тематики
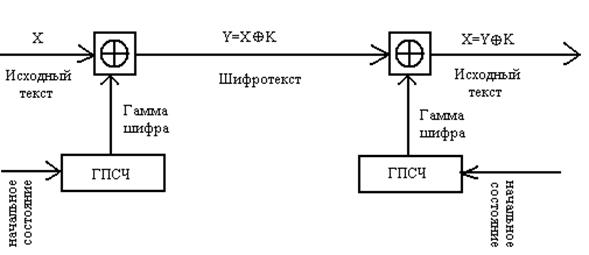
Поиск на нашем сайте Под гаммированием понимают наложение на открытые данные по определенному закону гаммы шифра [13]. Гамма шифра – псевдослучайная последовательность, вырабатываемая по определенному алгоритму, используемая для зашифровки открытых данных и дешифровки шифротекста. Общая схема шифрования методом гаммирования представлена на рис. 5.4.
Рис. 5.4. Схема шифрования методом гаммирования Принцип шифрования заключается в формировании генератором псевдослучайных чисел (ГПСЧ) гаммы шифра и наложении этой гаммы на открытые данные обратимым образом, например путем сложения по модулю два. Процесс дешифpования данных сводится к повторной генерации гаммы шифра и наложении гаммы на зашифрованные данные. Ключом шифрования в данном случае является начальное состояние генератора псевдослучайных чисел. При одном и том же начальном состоянии ГПСЧ будет формировать одни и те же псевдослучайные последовательности. Перед шифрованием открытые данные обычно разбивают на блоки одинаковой длины, например по 64 бита. Гамма шифра также вырабатывается в виде последовательности блоков аналогичной длины. Схему шифрования можно записать в этом случае в виде
где Дешифрование в данном случае осуществляется по следующей формуле:
Стойкость шифрования методом гаммирования определяется главным образом свойствами гаммы – длительностью периода и равномерностью статистических характеристик. Последнее свойство обеспечивает отсутствие закономерностей в появлении различных символов в пределах периода. Полученный зашифрованный текст является достаточно трудным для раскрытия в том случае, если гамма шифра не содержит повторяющихся битовых последовательностей. По сути дела гамма шифра должна изменяться случайным образом для каждого шифруемого блока. Обычно разделяют две разновидности гаммирования – с конечной и бесконечной гаммами. При хороших статистических свойствах гаммы стойкость шифрования определяется только длиной периода гаммы. При этом, если длина периода гаммы превышает длину шифруемого текста, то такой шифр теоретически является абсолютно стойким, т.е. его нельзя вскрыть при помощи статистической обработки зашифрованного текста, а можно раскрыть только прямым перебором. Криптостойкость в этом случае определяется размером ключа. В настоящее время разработано множество алгоритмов работы генераторов псевдослучайных чисел, которые обеспечивают удовлетворительные характеристики гаммы. Рассмотрим несколько примеров данных алгоритмов. Метод фон Неймана Данный метод является одним из первых способов генерации псевдослучайных чисел. Суть данного метода состоит в том, что каждое последующее случайное число получается путем возведения в квадрат предыдущего числа с отбрасыванием цифр младших и старших разрядов. Пусть A0 – четырехзначное число - начальное состояние ГПСЧ. Тогда i – ое псевдослучайное число Аi получается из предыдущего числа Аi-1 в результате следующих преобразований: 1. Возведение Аi-1 в квадрат, то есть нахождение числа 2. В качестве Аi выбирают четыре средние цифры числа Пример 5.10 Пусть A0 =1204, Однако метод фон Неймана является очень ненадежным, обладает множеством недостатков, в связи с чем используется достаточно редко.
Линейный конгруэнтный метод Данный генератор вырабатывает последовательность псевдослучайных чисел Y1, Y2,..., Yi-1, Yi,..., используя соотношение
где Yi – i -ое (текущее) число последовательности; Yi-1 – предыдущее число последовательности; a,b,m – константы; m – модуль; a – коэффициент; b – приращение; Y0 – начальное состояние ГПСЧ. Обычно значение модуля m берется равным 2n, либо простому числу. Приращение b должно быть взаимно простым с m, коэффициент a должен быть нечетным числом. Линейный конгруэнтный метод является одним из самых простейших методов генерации псевдослучайных последовательностей. Существует ряд методов, формирующих намного более криптографически стойкие псевдослучайные последовательности.
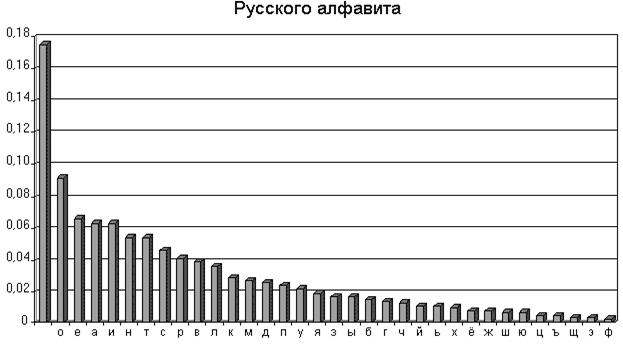
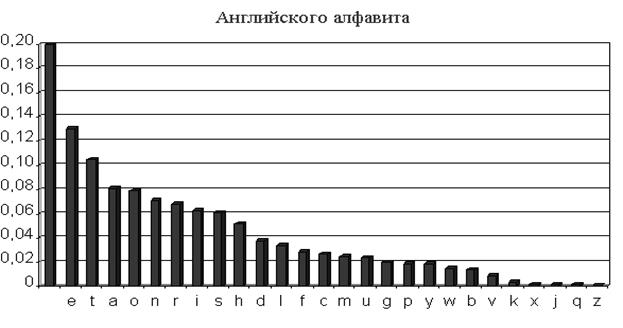
Элементы криптоанализа Любая попытка со стороны злоумышленника расшифровать шифротекст C для получения открытого текста М не имея подлинного ключа, называется криптоаналитической атакой. Криптоанализ – это наука о раскрытии исходного текста зашифрованного сообщения без доступа к ключу. Успешный анализ может раскрыть исходный текст или ключ. Он позволяет также обнаружить слабые места в криптосистеме, что в конечном счете ведет к тем же результатам. Криптоанализ, основанный на исследовании частотности символов в тексте Один из широко используемых методов криптоанализа для недостаточно криптостойких алгоритмов заключается в анализе частотности символов, встречающихся в зашифрованном тексте. Особенностью большинства искусственных языков (и всех естественных языков) является то, что они имеют характерное частотное распределение букв и других знаков. При этом, многие, недостаточно стойкие простейшие алгоритмы шифрования сохраняют частотность символов в тексте. В основном этот недостаток свойственен простейшим методам замены (например, шифру Цезаря и т.д.). Это распределение частотности дает криптоаналитику путь к раскрытию шифра. Частотное распределение букв русского и английского алфавита в художественных текстах представлено ниже
Исследовав зашифрованный текст и обнаружив, что наиболее часто встречаемый в нем символ – это «Б», а второй по встречаемости - «К», криптоаналитик может сделать вывод, что символ «Б» это «Пробел», а «К» это буква «о». Другим примером криптоаналитической атаки является атака по открытому тексту. Например, зная непрерывную часть открытого текста, большую или равную длине ключа для метода Вернама, можно вычислить ключ путем сложения по модулю 2 открытой и соответствующей ей закрытой части текста. Данный факт объясняет малую криптостойкость закрытых архивов ARJ, в которых система Вернама используется для криптографической защиты.
|
||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 2198; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

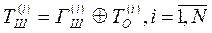
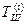 - i -ый блок шифротекста,
- i -ый блок шифротекста,  - i -ый блок гаммы шифра,
- i -ый блок гаммы шифра, 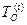 - i -ый блок открытого текста, N – количество блоков открытого текста.
- i -ый блок открытого текста, N – количество блоков открытого текста.
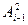 .
. =1449616. Тогда A1 =4496,
=1449616. Тогда A1 =4496, 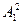 =20214016, A2 =2140 и т.д
=20214016, A2 =2140 и т.д