
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторная работа № 15. Математические функции мобр, мопред и мумножСодержание книги
Поиск на нашем сайте
Цель работы: использование встроенных математических функций МОБР, МОПРЕД и МУМНОЖ для вычисления обратной матрицы, определителя матрицы и перемножения матриц. Краткое описание теоретической части. Функция МОБР возвращает обратную матрицу для матрицы, хранящейся в массиве. Функция МОПРЕД возвращает определитель матрицы (матрица хранится в массиве). Функция МУМНОЖ возвращает произведение матриц (матрицы хранятся в массивах). Результатом является массив с таким же числом строк, как массив1, и с таким же числом столбцов, как массив2. Порядок выполнения работы. 1. Найдите матрицу, обратную данной:
Для этого: · введите элементы матрицы в диапазон ячеек А1:С3; · для получения обратной матрицы выделите несмежный диапазон ячеек такого же размера, например E1:G3, и введите формулу массива {=МОБР(А1:С3)}. Для заключения формулы в фигурные скобки после ввода формулы нажмите клавиши CTRL+Shift+Enter. 2. Вычислите определитель матрицы А. Для этого выделите любую свободную ячейку, например А5, и введите формулу =МОПРЕД(А1:С3) 3. Вычислите произведение матрицы А на матрицу В, где
Для этого: · введите элементы матрицы А в диапазон ячеек А10:С11; · введите элементы матрицы В в диапазон ячеек А13:С15; · выделите диапазон ячеек с таким же числом строк, как массив А, и с таким же числом столбцов, как массив В, например, E10:G11 и введите формулу ={МУМНОЖ(А10:С11; А13:С15)}; 4. Решите систему линейных уравнений с 3-мя неизвестными
методом обратной матрицы. Обозначим
Решение системы (1) в матричной форме имеет вид АХ = В, где: А – матрица коэффициентов; Х – столбец неизвестных; В – столбец свободных членов. При условии, что квадратная матрица (2) системы (1) невырожденная, т.е. ее определитель | А | ¹ 0, существует обратная матрица А · Найдем определитель | А | = 5 (см. п. 2). Для этого активизируем новый рабочий лист и введем элементы матрицы коэффициентов А в диапазон ячеек А1:С3. Выделим любую свободную ячейку, например А5, и введем формулу =МОПРЕД(А1:С3). · Так как | А | ¹ 0, то матрица А – невырожденная, и существует обратная матрица А
· Найдем решение системы в виде матрицы-столбца X = A ={МУМНОЖ(E1:G3; E6:E8)}; Получим:
т.е. решение системы (4; 2; 1). Контрольные вопросы. 1. Как получить обратную матрицу? 2. Как найти определитель матрицы? 3. Как найти произведение двух матриц? Дата защиты ____________ подпись преподавателя______________
|
|||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 373; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.218.124 (0.008 с.) |


 ;
;  .
. (1)
(1) ;(2)
;(2)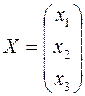 ;
;  .
. . Тогда решением системы методом обратной матрицы будет матрица-столбец X = A
. Тогда решением системы методом обратной матрицы будет матрица-столбец X = A 
 ,
,


