
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Графічний метод розв’язку ЗЛПСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Для розв’язку двовимірних ЗЛП, тобто задач з двома змінними, а також деяких тривимірних задач застосовують графічний метод, що грунтується на геометричній інтерпритації та аналітичних властивостях ЗЛП. Розглянемо таку задачу. Знайти екстремум (мінімум, максимум) функції:
за умов
Припустимо, що система (2.2) за умов (2.3) сумісна і многокутник її розв’язків обмежений. Згідно з геометричною інтерпретацією ЗЛП (2.1) кожне і- те обмеження-нерівність (2.2) визначає півплощину з граничною прямою Умова (2.3) невід’ємності змінних означає, що область допустимих розв’язків задачі належить першому квадранту системи координат двовимірного простору. Цільова функція ЗЛП геометрично інтерпретується як сім’я паралельних прямих
Деякі властивості ЗЛП (для графічного розв’язування):
1. Якщо ОДР – обмежена, то екстремум лінійної функції Z досягається принаймні в одній з вершин многокутника. 2. Якщо ОДР – необмежена, то екстремум функції Z або не існує, або досягається принаймні в одній з вершин ОДР. 3. Якщо оптимальне значення Z досягається одночасно у двох вершинах разом, то це ж саме екстремальне значення досягається в будь-якій точці відрізка, що з’єднує ці дві вершини (альтернативний оптимум).
Отже, розв’язати ЗЛП графічно означає знайти таку вершину многокутника розв’язків, у результаті підстановки координат якої в (2.1) лінійна цільова функція набуває найбільшого (найменшого) значення.
Алгоритм графічного методу: 1. Будуємо прямі лінії, рівняння яких дістаємо заміною в обмеженнях задачі (2.2) знаків нерівностей на знаки рівностей. 2. Визначаємо півплощини, що відповідають кожному обмеженню задачі. 3. Знаходимо многокутник розв’язків ЗЛП. 4. Будуємо вектор 5. Будуємо пряму 6. Переміщуючи пряму 7. Визначаємо координати точки, в якій цільова фукція набуває максимального (мінімального) значення, і обчислюємо екстремальне значення цільової функції в цій точці. Приклад 1. Знайти графічний розв’язок ЗЛП:
Рис.1
1. В (1), (2) замінюємо знаки нерівностей на знаки строгих рівностей: 3x+y=21, x+2y=10. Для спрощення побудови доцільно поділити обидві частини рівності на праву частину. Отримаємо:
Рівняння (1*) перетинає вісі координат в M(7,0), D(0,21), а (2*) – в L(10,0), F(0,5). Будуємо графіки прямих (1*), (2*) (рис.1). 2. Кожна з побудованих прямих поділяє площину системи координат на дві півплощини. Координати точок однієї задовольняють нерівність, що розглядається, а іншої – не задовольняють. Щоб визначити необхідну півплощину (на рис.1 її напрям позначено стрілками), потрібно взяти будь-яку точку і перевірити, чи задовольняютьїї координати зазначене обмеження. Якщо задовольняють, то півплощина, в якій міститься вибрана точка, є геометричним зображенням нерівності. У протилежному разі таким зображенням є інша півплощина. Умова невід’ємності змінних (3) обмежує ОДР задачі першим квадрантом системи координат. Переріз усіх півплощин визначає ОДР задачі.
3. OFKM – чотирикутник розв’язків ЗЛП. 4. Будуємо вектор у цільовій функції задачі. Вектор 5. Побудуємо лінію, що відповідає, наприклад, значенню
координат. 6. Переміщуючи пряму 7. Координати точки К визначаються перетином прямих (1) і (2):
Розв’язавши цю систему рівнянь, отримаємо:
Обчислюємо екстремальне значення цільової функції в К(6,4; 1,8):
Симплекс-метод (СМ) Основні означення:
1. Вектор x =(x1,...,xn) називається допустимим розв’язком ЗЛП, якщо його компоненти задовольняють обмеження (1.2)-(1.3) 2. Ненульовий допустимий розв’язок x -базисний (ДБР), якщо його додатнім компонентам xj відповідають лінійно незалежні вектори умов Aj (нульовий допустимий розв’язок будемо завжди вважати базисним). 3. Система m лінійно незалежних векторів умов, що включає вказані вектори Aj називається базисом. 4. Вектори базису утворюють базисну матрицю. 5. ЗЛП називається канонічною, якщо її обмеження (1.2) мають канонічну форму: x1+ + a1,m+1 xm+1+...+a1nxn=a10 ....................................................... xj+ +aj,m+1 xm+1+...+ajnxn=aj0 ........................................................ xm + am1xm+1+...+amnxn=am0 xj³0, j=1,...,n 6. Щоб перетворити задачу із загальної у стандартну форму, треба зробити наступну послідовність дій: 1) у нерівність £ з (1.2) потрібно ввести додаткову змінну yj (яка також називається базисною) з коефіцієнтом 1. При цьому нерівність перетворюється в рівність, коефіцієнт в цільовій функції при новій змінній дорівнює нулю і на нову змінну накладається умова невід’ємності. 2) у нерівність ³ з (1.2) потрібно ввести додаткову змінну yj з коефіцієнтом -1 (всі інші дії аналогічні п.1). 3) якщо на деяку змінну xj не накладено умову невід’ємності, то ця змінна замінюється різницею двох змінних yk-yk+1, на які вже накладено умову невід’ємності. При цьому заміну xj® yk-yk+1 потрібно зробити в цільовій функції (1.1) і в системі обмежень (1.2).
Приклад 2. Нехай потрібно звести до стандартної форми наступну задачу: x1+ 2x2 - 3x3®min x1+ x2 = 8 2x1 + x3 £ 6 x1 +2x3 ³ 2 x1, x2 ³ 0 Перше обмеження залишаємо без змін. У друге обмеження додаємо змінну x4 зі знаком +, а у третє- змінну x5 зі знаком -. Оскільки на змінну x3 не накладено умову невід’ємності, то замінюємо її різницею двох невід’ємних змінних (наприклад x3-x6). Таким чином, задача приймає наступний вигляд: x1+ 2x2 -3x3 + 3x6®min x1 + x2 =8 2x1 +x3 +x4 -x6 =6 x1 +2x3 -x5-2x6 =2 xj ³0, j=1,..,6
Стандартна ЗЛП (1.1)-(1.3) може також зводитись до канонічної форми за допомогою так званого методу штучних змінних, суть якого полягає у наступному. Розглядається допоміжна задача (назвемо її y-задачею) з такою ж самою системою обмежень, як і М-задача, але цільова функція має вигляд: L*(x)=y1+...+ym®min. Допоміжна задача розв’язується симплекс-методом. При цьому можуть виникнути такі випадки: 1) Для оптимального розв’язку L*(x)=0 (тобто жодна з yj не є базисною). Тоді відкидаємо всі yj і розв’язуємо одержану задачу симплекс-методом (оскільки для неї вже побудовано початковий допустимий базисний розв’язок). 2) Для оптимального розв’язку L*( x )>0 (тобто принаймні одна з yj не є базисною). Тоді вихідна ЗЛП не має розв’язків.
Перед застосуванням М-методу або методу штучного базису можна зробити декілька жорданових перетворень вихідної матриці умов. Діючи таким чином, можна зменшити кількість штучних змінних, а іноді й уникнути застосування вказаних методів. Жорданові перетворення робляться таким чином: 1) Для деякого стовбця k обчилюється для aik>0 відношення qi=ai0/aik і визначається і, що задовольняє співвідношенню i=argmin qi, i: aik>0. 2) Елемент aik вибирається за розв’язуючий і робиться перетворення Жордана-Гауса. 3) Розглядається інший стовбець, який не є базисним і для нього визначається i (як описано в п. 1). Якщо визначене i не співпадає з номерами рядків, в яких вже є базисні змінні, то переходимо до п. 2, а якщо співпадає - то вибираємо інший небазисний стовбець. Якщо в результаті послідовності дій 1)-3) одержано m базисних змінних, то застосовувати метод штучного базису або M-метод не потрібно і одразу переходимо до розв’язку задачі симплекс-методом. Якщо кількість одержаних базисних змінних менша за m, то штучні змінні додамо лише у рядки, в яких немає базисних змінних, і застосовуємо метод штучного базису або M-метод. Алгoритм симплекс-метoду
На кожному кроцi СМ виконуються такі дії (розрахункові формули наводяться лише для першого кроку). 1. Розглядається ДБР x=(a10,...,am0,0,...,0). Обчислюються відносні оцінки (симплекс-рiзницi) Dj небазисних змінних xj, j=m+1,...,n, за формулою: Dj=cj – (cб, Aj), де cб=(c1,...,cm), Aj — вектор умов, що відповідає змінній xj (відносні оцінки базисних змінних дорівнюють нулю). Якщо для всіх j=1,...,n, виконується умова Dj³0, то ДБР x є оптимальним розв'язком КЗЛП. Якщо до того ж усі штучні змінні дорівнюють нулю, то, відкидаючи їх, отримаємо оптимальний розв'язок вихідної ЗЛП; інакше вихідна ЗЛП не має розв'язкiв (її допустима область порожня). Якщо існує таке j, що Dj<0, а вектор умов Aj не має додатніх компонент, то ЗЛП не має оптимального розв'язку (її цільова функція L(x) не обмежена знизу на допустимому многограннику розв'язкiв). Кiнець обчислень. 2. Якщо існують індекси j, для яких Dj<0, а відповідні вектори умов Aj мають додатні компоненти, то знаходять k за формулою k=argminDj, j: Dj<0 i, обчислюючи для aik>0 відношення qi=ai0/aik, визначають i, що задовольняє співвідношення i=argminqi, i: aik>0 3. Переходять до нового ДБР, шляхом уведення до базису вектора Ak i виведення з базису вектора Ai. Такий перехід здійснюється за допомогою симплекс-перетворень (елементарних перетворень Жордана-Гаусса) з ведучим елементом aik над елементами розширеної матриці умов (1.2). Перехiд до пункту 1.
Далі буде розглянуто декілька прикладів розв’язку задач (в усіх задачах, що розглядаються нижче, всі змінні невід’ємні).
Задача 1. x1+x2+x3®min x1 -x4 -2x6=5 x2 + 2x4-3x5+ x6=3 x3+2x4-5x5+2x6=5
Складаємо симлекс-таблицю:
На першому кроці базисними змінними є x1,x2 та x3, отже вектор С Б має координати (1,1,1). Оцінки при базисних змінних дорівнюють нулю. Для інших змінних оцінки треба обчислити за формулою Dj=cj-( С Б, X j). Таким чином, D4=0-((1,1,1),(-1,2,3))=-3; D5=0-((1,1,1),(0,-3,-5))=8; D6=0-((1,1,1),(-2,1,2))=-1. Далі вибираємо стовпчик з максимальною за модулем від’ємною оцінкою (тобто 4-й). Для 4-го стовпчика визначаємо мінімальне Q: мінімум досягається для i=2. Вибираємо елемент (2;4) за розв’язуючий та робимо перетворення Жордана-Гауса. У другій таблиці всі Xопт=(13/2; 0; 2; 3/2; 0; 0; 0), Fmin=13/2+2=17/2. Нехай треба знайти максимум цільової функції для цієї ж самої задачі. У цьому випадку треба замінити знак коефіцієнтів цільової функції на протилежний і симплекс-таблиці матимуть такий вигляд:
З першої таблиці видно, що D 5 <0, однак всі інші елементи 5-го стовпця від’ємні, зачить цільова функція необмежена на допустимій області. Задача 2.
x1+ 2x2+ x4®min x1+ x2+2x3- x4 = 2 2x1+ x2- 3x3+x4 = 6 x1+ x2+ x3+x4 = 7
У цій задачі, на відміну від попередньої, немає початкового допустимого базисного розв’язку. Розглянемо три методи його пошуку.
1) Метод жорданових перетворень.
Таким чином, побудовано початковий допустимий базисний розв’язок і задача повністю підготовлена до застосування симплекс-методу:
Оскільки всі D³0, то знайдений допустимий базисний розв’язок є оптимальним, Xопт=(3; 0; 1; 3), Fmin=3+1=4. 2) Метод штучних змінних. Допоміжна задача для побудови допустимого базисного розв’язку вихідної задачі має вигляд:
y1+ y2+ y3®min x1+ x2+2x3 -x4 + y1 =2 2x1+ x2 -3x3+x4 + y2 =6 x1+ x2+ x3+x4 +y3=7
Таким чином, всі D³0, отже знайдено розв’язок допоміжної задачі, при цьому всі yj виведено з базису, отже відкидаючи стовпці yj, маємо ДБР для вихідної задачі (який, доречі, співпадає з ДБР, який було знайдено методом жорданових перетворень). Знайдений розв’язок задачі симплекс-методом повністю співпадає з наведеним вище.
3) М-метод. Допоміжна М-задача має такий вигляд: x1+ 2x2+ x4+ My1+My2+ My3®min x1+ x2+2x3-x4 + y1 =2 2x1+x2-3x3+x4 + y2 =6 x1+ x2+ x3+x4 +y3=7 тобто штучні змінні yj вводяться в нерівності і водночас вводяться в цільову функцію з коефіцієнтами M (де М-деяке достатньо велике число).
Послідовність симплекс-таблиць має вигляд:
Таким чином, всі D³0, отже знайдено оптимальний розв’язок допоміжної задачі, при цьому в базисі немає штучних змінних, отже знайдено оптимальний розв’язок вихідної задачі, який співпадає зі знайденим у попередньому випадку.
Задача 3. x1- 2x2+ 3x3®min 2x1+ 3x2+4x3 =1 -2x1+ x2 +3x3 =2 Метод штучних змінних Складаємо допоміжну задачу: y1+ y2®min 2x1+ 3x2+4x3 + y1 =1 -2x1+ x2 +3x3 + y2 =2
На останній ітерації всі всі D³0, отже знайдено оптимальний розв’язок допоміжної задачі, при цьому в базисі є штучна змінна y2, отже вихідна задача не має розв’язку.
M-метод
Складаємо допоміжну задачу:
x1 -2x2+3x3 +My1+ My2®min 2x1+ 3x2+4x3 + y1 =1 -2x1+ x2 +3x3 + y2 =2
Висновки повністю співпадають з попереднім випадком. Задача 4. 6x1+ 4x2 ®min 2x1+ x2 ³ 3 x1 - x2 £ 1
Таким чином, система обмежень набуває вигляду 2x1+ x2 -x3 = 3 x1 - x2 +x4 =1 Якщо всі нерівності мали знак £, то перетворена задача мала б канонічну форму. В іншому разі треба звести задачу до неї одним з наведених вище методів. В данному випадку достатньо зробити одне жорданове перетворення:
Оптимальний розв’язок має вигляд: x1=4/3, x2=1/3, Fmin=6*(4/3)+4*(1/3)=28/3
Двоїстість у ЛП Поняття двоїстості.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 434; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.195.180 (0.012 с.) |

 (2.1)
(2.1)

 (2.3)
(2.3) (і=1, 2, …, m). Системою обмежень (2.2) описується спільна частина, тобто множина точок, координати яких задовольняють всі обмеження задачі. Таку множину точок називають многокутником розв’язків, або областю допустимих розв’язків ЗЛП (ОДР).
(і=1, 2, …, m). Системою обмежень (2.2) описується спільна частина, тобто множина точок, координати яких задовольняють всі обмеження задачі. Таку множину точок називають многокутником розв’язків, або областю допустимих розв’язків ЗЛП (ОДР).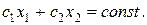
 що задає напрям зростання значень цільової функції задачі.
що задає напрям зростання значень цільової функції задачі. , перпендикулярну до вектора
, перпендикулярну до вектора 
 (для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину многокутника розв’язків, де цільова функція досягає екстримального значення.
(для задачі максимізації) або в протилежному напрямі (для задачі мінімізації), знаходимо вершину многокутника розв’язків, де цільова функція досягає екстримального значення.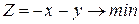
 , (1)
, (1) , (2)
, (2)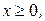
 . (3)
. (3) y
y


 D
D




 F
F




 2 K
2 K







 або
або 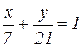 , (1*)
, (1*)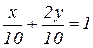 або
або  . (2*)
. (2*) компонентами якого є коефіцієнти при змінних
компонентами якого є коефіцієнти при змінних .
. Це буде пряма
Це буде пряма , яка перпендикулярна до вектора
, яка перпендикулярна до вектора 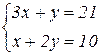

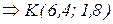 .
. .
. ,
, , тобто знайдено оптимальний розв’язок, який знаходимо із стовпця A0 останньої таблиці:
, тобто знайдено оптимальний розв’язок, який знаходимо із стовпця A0 останньої таблиці: Þ
Þ 
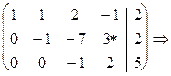


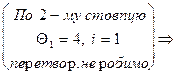

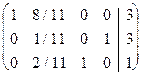
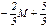





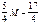

 Щоб привести задачу до стандартного вигляду, треба додати у обмеження-нерівності додаткові (або балансові змінні) і перетворити їх таким чином на обмеження-рівності. При цьому у неріності £ балансові змінні додаються зі знаком +, а в ³ зі знаком -.
Щоб привести задачу до стандартного вигляду, треба додати у обмеження-нерівності додаткові (або балансові змінні) і перетворити їх таким чином на обмеження-рівності. При цьому у неріності £ балансові змінні додаються зі знаком +, а в ³ зі знаком -. Þ
Þ 



