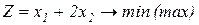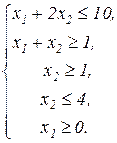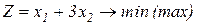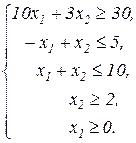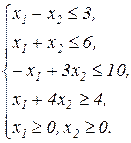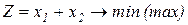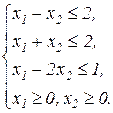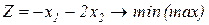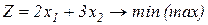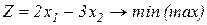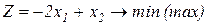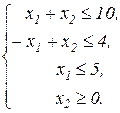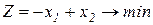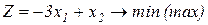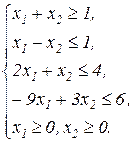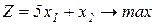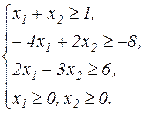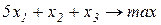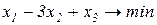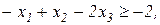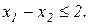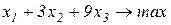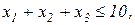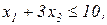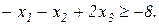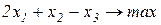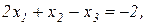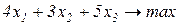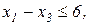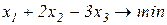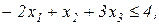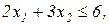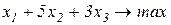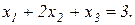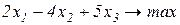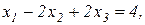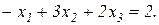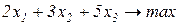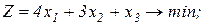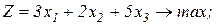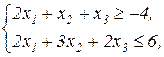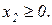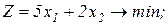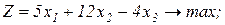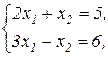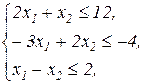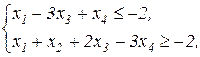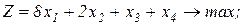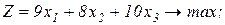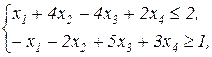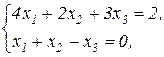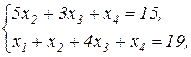Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод пiвнiчно-захiдного кутаСодержание книги Поиск на нашем сайте
Метод складається з однотипних кроків, тому його формальний виклад дамо лише для 1-го кроку. Заповнюємо пiвнiчно-захiдну клітинку таблиці, покладаючи x11 = min{ a1, b1 }. Можливі три випадки: 1. a1 < b1, тоді x11 = a1 i викреслюється 1-й рядок таблиці; 2. a1 > b1, тоді x11 = b1 i викреслюється 1-й стовпець таблиці; 3. a1 = b1, тоді x11 = a1 = b1 i викреслюється як 1-й рядок, так i 1-й стовпець. В останньому випадку в одну з викреслених клітинок заноситься нульове базисне перевезення (відповідний вихідний допустимий базисний розв'язок буде виродженим). В усіх випадках після заповнення базисної клітинки об'єми запасів a1 i потреб b1 зменшують на величину, що дорівнює x11. Кiнець кроку. На кожному з наступних кроків розглядається «обрізана» транспортна таблиця, тобто викреслені рядки i стовпцi ігноруються. Задача 7. Побудувати опорний план ТЗ (або вихідний ДБР): Таблиця 2
Заповнення починається з клітинки Таблиця 3
Одержаний план є опорним, бо з його ненульових перевезень неможливо скласти замкнений маршрут (цикл), і він задовольняє умовам задачі. Метод мінімального елемента Кількість ітерацій при розв’язуванні ТЗ можна скоротити, якщо перший опорний план будувати за методом мінімального елемента. Метод відрізняється від попереднього тим, що замість пiвнiчно-захiдної клітинки на кожному кроцi вибирається клітинка з найменшим значенням транспортних витрат cij. Задача 7. Розв’яжемо задачу 7 з попереднього пункту методом мінімального елемента. На кожному кроцi вибирається клітинка з найменшим значенням транспортних витрат cij. Оскільки Таблиця 4
Очевидно, що цей опорний план є ефективнішим за план, наведений у табл.2. Метод викреслювання
Метод застосовується при побудові циклу. На кожному кроцi методу в транспортній таблиці викреслюється або рядок, або стовпець, які в подальшому ігноруються. Викреслювати належить рядки (стовпцi), які мають тільки одну базисну клітинку. Невикресленi клітинки транспортної таблиці утворюють цикл. Метод подвійної переваги Перед початком заповнення таблиці необхідно позначити клітинки, які мають найменшу вартість у рядках і стовпчиках. Таблицю починають заповнювати з клітинок, позначених двічі (як мінімальні і в рядку, і в стовпчику). Далі заповнюють клітинки, позначені один раз (як мінімальні або в рядку, або в стовпчику), а вже потім – за методом мінімального елемента.
Метод потенціалів Алгоритм методу потенціалів 1. Знаходиться вихідний допустимий базисний розв'язок (ДБР), наприклад, за допомогою одного із згаданих вище методів. 2. В подальшому метод потенціалів складається з однотипних кроків, на кожному з яких: i) Обчислюються потенціали рядків ui, i=1,...,m, i стовпцiв vj, j=1,...,n, транспортної таблиці як розв'язок системи vjui = cij, де i та j приймають такі значення, що клітинки (i,j) базисні. ii) Обчислюються оцінки змінних xij для всіх небазисних клітинок (i,j) за формулою ij = cijvj + ui (оцінки базисних змінних нульові). iii) Знайдені оцінки ij перевіряються на невiд'ємнiсть. Якщо всі ij0, i=1,...,m, j=1,...,n, то поточний ДБР оптимальний. Інакше переходять до поліпшення ДБР (пункт iv)). iv) Визначають клітинку (k,l) з мінімальною від'ємною оцінкою, i приєднують її до сукупності базисних. Знаходять цикл (наприклад, методом викреслювання). Подiляють цикл на додатний i від'ємний пiвцикли, послідовно позначаючи клітинки - вершини циклу знаками «+» i «», починаючи з клітинки (k,l), яку першою відносять до додатного пiвциклу, наступну за нею до від'ємного, третю до додатного i т. д. Серед клітинок від'ємного пiвциклу визначають клітинку (s,r) з мінімальною величиною перевезення xij (якщо таких клітинок кілька, то вибирають тільки одну з них). Покладають = xsr. Збiльшують на значення перевезення xij в клітинках додатного пiвциклу i зменшують їх на те ж значення в клітинках від'ємного пiвциклу. В результаті здійснення вказаних процедур клітинка (k,l) вводиться до сукупності базисних, а клітинка (s,r) перестає бути базисною (на ній розривають цикл). Кiнець кроку. Задача 8. Методом потенціалів ТЗ, дані для якої наведені в таблиці 2. З таблиці 4 візьмемо і початковий базисний розв’язок, побудований методом мінімального елемента. Усі ці дані перенесені в таблицю 5. Таблиця 5
Крім цього до таблиці 5 занесені потенціали Для введення до числа базисних вибирається клітинка Зауважимо, що при розв’язуванні системи для знаходження потенціалів Таблиця 6
Таблиця 7
У таблиці 7 наведені результати обчислень для наступної ітерації. У цьому випадку при розв’язуванні системи для знаходження потенціалів покладено Як бачимо, критерій оптимальності виконується, отже,
є оптимальним розв’язком ТЗ, Завдання для самостійної роботи для студентів заочної та денної форми навчання:
Завдання1. Графічним методом визначити оптимальні розв’язки ЗЛП.
1.1.
1.2.
1.3.
1.4.
1.5.
1.6.
1.7.
1.8.
1.9.
1.10.
1.11.
1.12.
1.13.
1.14.
1.15.
1.16.
1.17.
1.18.
1.19.
1.20.
1.21.
1.22.
1.23.
1.24.
1.25.
1.26.
1.27.
1.28.
1.29.
1.30.
1.31.
1.32.
1.33.
1.34.
1.35.
1.36. 1.37.
1.38.
Завдання 2. Розв’язати симплекс-методом ЗЛП. В усіх задачах, що пропонуються нижче, всі змінні невід’ємні. 2.1. 2x1+x2-x3-x4®min x1+x2+2x3-x4=2 2x1+x2 -3x3+x4=6 x1+x2+ x3 +x4=7 2.2. 2x1-4x2®min 8x1 -5x2£16 x1+3x2³2 2x1 +7x2£9 2.3. 7x1+5x2®max 7x1+5x2³7 7x1 -5x2³35 x1 - x2£0 2.4. x1-2x2+3x3®min 2x1+3x2 +4x3=1 -2x1+ x2 +3x3=2 2.5. 2x1-3x2®max 5x1+2x2³10 x1+3x2£12 2.6. 6x1+4x2®min 2x1+x2³3 x1 -x2£1 2.7. 4x1+5x2+9x3+11x4®max x1+ x2+ x3+ x4 £15 7x1+5x2+ 3x3+ 2x4£80 3x1+5x2+10x3+15x4£60 2.8. x1 - x2-2x3 +x4®max 2x1+ x2+ 2x3 -x4 =2 -3x1+ x2 +2x3+x4 =6 x1+ x2+ x3+x4 =7 2.9. 4x1+ x2-2x3 -x4- x5®min x3 -x4+ x5=1 x2 +2x4 -x5=1 x1+2x2+ 2x5=4 2.10. x1+2x2 +3x3-x4®max x1+2x2+ 3x3 =15 2x1+ x2 -3x3 =20 x1+ 2x2+x4 =10 2.11.
2.12.
2.13.
2.14.
2.15.
2.16.
2.17.
2.18.
2.19.
2.20.
2.21.
2.22.
2.23.
2.24.
2.25.
2.26.
2.27.
2.28.
2.29.
2.30.
2.31.
2.32.
2.33.
Завдання 3. 2.34.
2.35.
2.36.
2.37.
2.38.
У наведених задачах записати двоїсту задачу до поставленої ЗЛП.
3.1.
3.2.
3.3.
3.4.
3.5.
3.6.
3.7.
3.8.
3.9.
3.10.
3.11.
3.12.
3.13.
3.14.
3.15.
3.16.
3.17.
3.18.
3.19.
3.20.
3.21.
3.22.
3.23.
3.24.
3.25.
3.26.
3.27.
3.28.
3.29.
3.30.
3.31.
3.32.
3.33.
3.34.
Завдання 4. Розв'язати двоїстим симплекс-методом ЗЛП. В усіх задачах, що пропонуються далі, всі змінні невід'ємні.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 165; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.181.112 (0.012 с.) |

 . Оскільки
. Оскільки 
 , то викреслюється перший рядок таблиці,
, то викреслюється перший рядок таблиці, 
 . Переходимо до клітинки
. Переходимо до клітинки  . Заносимо в клітинку
. Заносимо в клітинку  і викреслюємо перший стовпчик,
і викреслюємо перший стовпчик, 
 . Переходимо до клітинки
. Переходимо до клітинки  :
:  , викреслюється другий рядок,
, викреслюється другий рядок, 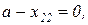
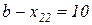 . Наступною буде клітинка
. Наступною буде клітинка  :
:  , викреслюємо другий стовпчик,
, викреслюємо другий стовпчик, 
 . Переходимо до клітинки
. Переходимо до клітинки  :
: 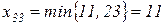 , викреслюється третій рядок,
, викреслюється третій рядок, 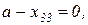
 . Переходимо до клітинки
. Переходимо до клітинки 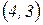 :
: 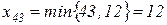 ,
, 
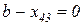 . Наступна клітинка
. Наступна клітинка  :
:  ,
, 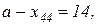
 . Остання клітинка
. Остання клітинка  :
: 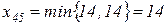 ,
, 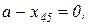
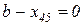 .
. , то заповнення починається з клітинки
, то заповнення починається з клітинки  :
: 

 . Переходимо до клітинки
. Переходимо до клітинки 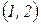 . Заносимо в клітинку
. Заносимо в клітинку 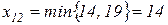 і викреслюємо другий рядок,
і викреслюємо другий рядок, 
 . Переходимо до клітинки
. Переходимо до клітинки  , викреслюється третій стовпчик,
, викреслюється третій стовпчик, 
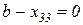 . Наступною буде клітинка
. Наступною буде клітинка  , викреслюємо третій рядок,
, викреслюємо третій рядок,  . Переходимо до клітинки
. Переходимо до клітинки  , викреслюється п’ятий стовпчик,
, викреслюється п’ятий стовпчик, 
 , викреслюється четвертий стовпчик,
, викреслюється четвертий стовпчик, 
 :
:  , викреслюється другий стовпчик,
, викреслюється другий стовпчик, 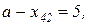
 . Остання клітинка
. Остання клітинка 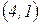 :
:  ,
, 
 .
.

 P3
P3
 P4
P4
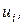
 (останній стовпець),
(останній стовпець), 
 (останній рядок), що є розв’язком системи
(останній рядок), що є розв’язком системи 

 - базисне, де покладено
- базисне, де покладено  У верхніх лівих кутах кожної з клітинок записані величини
У верхніх лівих кутах кожної з клітинок записані величини  . Бачимо, що розглядуваний базисний розв’язок не є оптимальним.
. Бачимо, що розглядуваний базисний розв’язок не є оптимальним. . Новий базисний розв’язок і відповідні обчислення наведені у таблиці 6.
. Новий базисний розв’язок і відповідні обчислення наведені у таблиці 6.

 P1
P1
 P2
P2
 P4
P4