
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Постановка транспортної задачіСодержание книги Поиск на нашем сайте
В кожному з пунктів Pi, i=1,...,m, виробляється ai одиниць деякого однорідного продукту, а в кожному з пунктів Qj, j=1,...,n, споживається bj одиниць того ж продукту. Можливе транспортування продукту із кожного пункту виробництва Pi в кожний пункт споживання Qj. Вартiсть перевезення одиниці продукту з пункту Pi в пункт Qj відома i складає cij одиниць. Ці дані наведені в табл. 1. В даній таблиці в рядках записані постачальники, в стовпцях – споживачі. Перетин рядків і стовпців створює клітинки, в яких наведено інформацію про перевезення продукції від і- го постачальника до j- го споживача. Кожна така клітинка поділена по діагоналі, у верхній частині її записані затрати на перевезення одиниці вантажу від і- го постачальника до j- го споживача - Вважаючи, що сумарний об'єм виробництва дорівнює сумарному об'єму споживання, потрібно скласти план перевезень продукту, що мiнiмiзує сумарні транспортні витрати. Таблиця 1
Математична модель транспортної задачі має вигляд:
L(x) = c11 x11 +...+ c1n x1n +...+ cm1 xm1 +...+ cmn xmn min, xi1 +...+ xin = ai, i=1,...,m, x1j +...+ xmj = bj, j=1,...,n, xij0, i=1,...,m, j=1,...,n, a1 +...+ am = b1 +...+ bn. Остання умова визначає збалансовану транспортну задачу. В запропонованій моделі назвемо вектор x = (x11,...,x1n,...,xm1,...,xmn)вектором перевезень, вектор b = (a1,...,am,b1,...,bn)твектором запасiв - потреб, вектор A ij= (0,...,0,1,0...,0,0,...,0,1,0,...,0)твектором комунікації PiQj (вектор A ij має розмірність m + n, причому перша одиниця стоїть на i- у місці, а друга на m + j -у) i, нарешті, вектор c = (c11,...,c1n,...,cm1,...,cmn)вектором транспортних витрат. Основні означення Оскiльки транспортна задача є частинним випадком задачі лінійного програмування, для неї мають силу всі загальні означення останньої. Зокрема, зауважене відноситься також i до допустимого базисного розв'язку (ДБР), як невиродженого, так i виродженого. Послiдовнiсть комунікацій, серед яких немає однакових, вигляду:
називається маршрутом, що зв'язує пункти Маршрут, до якого додана комунікація
Комунiкацiя PiQj називається основною комунікацією розв'язку x, якщо відповідна їй компонента розв'язку xij > 0. Подібні означення мають місце i для клітинок транспортної таблиці. Властивості транспортної задачі: 1. Збалансована транспортна задача завжди допустима i має оптимальний розв'язок. 2. Ранг матриці A обмежень транспортної задачі дорівнює m+n1, внаслідок чого допустимий базисний розв'язок задачі містить не більше m+n1 ненульових перевезень xij. 3. Якщо в транспортній задачі всі числа ai, i=1,...,m, bj, j=1,...,n, цілі, то хоча б один оптимальний розв'язок задачі цiлочисельний. Основні теореми: 1. Розв'язок транспортної задачі базисний, якщо з його основних комунікацій неможливо скласти замкнений маршрут (цикл). 2. ДБР x =(xij, i=1,...,m, j=1,...,n) оптимальний тоді i тільки тоді, коли існують потенціали ui, vjтакі, що vj ui = cij, якщо xij - базисне перевезення, vj ui cij, якщо xij - небазисне перевезення.
Методи пошуку вихідного ДБР
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 185; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.68.154 (0.009 с.) |

 а в нижній – обсяг вантажу -
а в нижній – обсяг вантажу - 















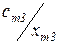


 i
i  .
. , називається замкненим маршрутом (циклом).
, називається замкненим маршрутом (циклом).


