Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Правила побудови двоїстих задачСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Кожній ЗЛП відповідає двоїста, що формується за допомогою певних правил безпосередньо з умови прямої задачі. Якщо пряма ЗЛП має вигляд:
то двоїста задача записується так:
за обмежень
Отже, двоїста ЗЛП утворюється з прямої задачі за такими правилами: 1. Кожному обмеженню прямої задачі відповідає змінна двоїстої задачі. Кількість невідомих двоїстої задачі дорівнює кількості обмежень прямої задачі. 2. Кожній змінній прямої задачі відповідає обмеження двоїстої задачі, причому кількість обмежень дорівнює кількості невідомих прямої задачі. 3. Якщо цільова функція прямої задачі задається на пошук найбільшого значення (max), то цільова функція двоїстої задачі – на визначення найменшого значення (min), і навпаки. 4. Коефііцієнтами при змінних в цільовій функції двоїстої задачі є вільні члени системи обмежень прямої задачі: 5. Правими частинами системи обмежень двоїстої задачі є коефіцієнти при змінних в цільовій функції прямої задачі: 6. Матриця
що складається з коефіцієнтів при змінних у системі обмежень прямої задачі, і матриця коефіцієнтів в системі обмежень двоїстої задачі
утворюються одна з одної транспонуванням, тобто заміною рядків стовпчиками, а стовпчиків – рядками. Двоїсті пари ЗЛП бувають симетричні та несиметричні. У симетричних задачах обмеження прямої та двоїстої задач є нерівностями, а змінні обох задач можуть набувати лише невід’ємних значень. У несиметричних задачах обмеження прямої задачі можуть бути записані як рівняння, а двоїстої – лише як нерівності. У цьому разі відповідні змінні двоїстої задачі набувають будь-якого значення, не обмеженого знаком. Різні можливі форми прямих ЗЛП та відповідні їм варіанти моделей двоїстих задач наведено далі.
Пряма задача Двоїста задача Симетричні
Несиметричні
Приклад 3. До наведеної ЗЛП записати двоїсту задачу:
За відповідними правилами побудуємо двоїсту задачу:
Зауважимо, що задачі несиметричні, і тому змінна
Приклад 4. До наведенної ЗЛП записати двоїсту задачу:
Перш ніж записати двоїсиу задачу, необхідно пряму задачу звести до відповідного вигляду. Оскільки цільова функція Z максимізується і в системі обмежень є нерівності, то вони повинні мати знак “
Тепер за відповідними правилами складемо двоїсту задачу:
Записані задачі симетричні.
Двоїстий симплекс-метод Двоїстий симплекс-метод (ДСМ) безпосередньо застосовується до розв'язування майже канонічної задачі лінійного програмування (МКЗЛП), яка формулюється таким чином: Знайти вектор x = (x1,...,xn), що мiнiмiзує лінійну функцію L (x) = c1x1+... + cnxn (3.1) i задовольняє систему лінійних обмежень xi + ai,m+1xm+1 +... + ainxn = ai0, i=1,...,m, (3.2) xj ³ 0, j=1,...,n, (3.3) (компоненти ai0 вектора обмежень A 0 можуть бути від'ємними) при додатковій умові: відносні оцінки (симплекс-рiзницi) D jзмінних xjневід'ємні. Вектор x =(x1,...,xn) називається майже допустимим базисним розв'язком (МДБР) МКЗЛП, якщо його компоненти задовольняють обмеження (3.2), i ненульовим компонентам xj відповідають лінійно незалежні вектори умов A j. Базис i базисна матриця МДБР визначаються подібно тому, як це робиться для СЗЛП. МКЗЛП є частинним випадком СЗЛП. Iснують методи зведення довільної ЗЛП до майже канонічного вигляду.
Ознака оптимальності:
Якщо на деякому кроцi ДСМ компоненти МДБР x * невід'ємні, то x * — оптимальний розв'язок МКЗЛП. Ознака відсутності розв'язку:
Оптимального розв'язку МКЗЛП не існує, якщо на якому-небудь кроцi ДСМ в рядку з ai0 < 0 всі компоненти aij ³ 0, j=1,...,n. В цьому випадку допустима множина розв'язкiв МКЗЛП порожня.
Алгоритм двоїстого симплекс-методу: На кожному кроцi ДСМ виконуються такі дії (розрахункові формули наводяться лише для першого кроку). 1. Розглядається МДБР x =(a10,..., am0,0,...,0). Обчислюються відносні оцінки (симплекс-рiзницi) Dj небазисних змінних xj, j=m+1,...,n, за формулою: D j = cj – (c б, A j), де c б =(c1,..., cm), A j — вектор умов, що відповідає змінній xj (відносні оцінки базисних змінних дорівнюють нулю). Якщо для всіх i=1,...,m виконується умова ai0 ³ 0, то МДБР x буде оптимальним розв'язком МКЗЛП. Кiнець обчислень. Якщо існує таке i, що ai0 < 0, а коефіцієнти aij ³ 0, j=1,...,n, то МКЗЛП не має допустимих розв'язкiв. Кiнець обчислень.
2. Якщо існують індекси i, для яких ai0 < 0, а серед відповідних компонент aij, j=1,...,n, є від'ємні, то знаходять l: l =argmin ai0, i: ai0 < 0 обчислюють відношення gj = – D j/alj для всіх alj < 0 та визначають k: k =argmin gj. i: alj < 0 3. Переходять до нового МДБР, виключаючи з базису вектор A l i вводячи до базису вектор A k. Згаданий перехід здійснюється за допомогою симплекс-перетворень (елементарних перетворень Жордана-Гаусса з ведучим елементом alk) над елементами розширеної матриці умов. Перехiд до пункту 1. Задача 5. Розв’язати двоїстим симплекс-методом ЗЛП:
Наведена ЗЛП є МКЗЛП. Її розв’язування ведеться в симплекс-таблицях, які незначним чином відрізняються від звичайних симплекс-таблиць.
Оптимальний розв’язок задачи:
При цьому
Задача 6.
Наведена ЗЛП є МКЗЛП.
Оптимального розв'язку МКЗЛП не існує, оскільки на 2-му кроцi ДСМ в рядку з ai0 < 0, (і=1, 2) всі компоненти aij ³ 0, j=1,...,6. В цьому випадку допустима множина розв'язкiв МКЗЛП порожня. ЗЛП розв’язку не має.
ТРАНСПОРТНА ЗАДАЧА
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-10; просмотров: 414; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.82.168 (0.009 с.) |









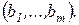




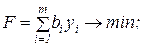

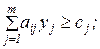




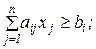







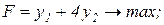


 що відповідає рівнянню в системі обмежень прямої задачі, може мати будь-який знак, а змінна
що відповідає рівнянню в системі обмежень прямої задачі, може мати будь-який знак, а змінна  - лише невід’ємна.
- лише невід’ємна.


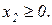
 ”. Тому перше обмеження моделі помножимо на (-1). При цьому знак нерівності зміниться на протилежний. Отримаємо:
”. Тому перше обмеження моделі помножимо на (-1). При цьому знак нерівності зміниться на протилежний. Отримаємо: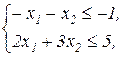
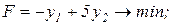







 .
.