
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Какие физические постоянные являются фундаментальными и каково их число.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте С -класс ("ядро" современной физики) составляют наиболее фундаментальные постоянные, являющиеся абсолютными масштабами физических величин, такие как скорость света с и постоянная Планка h ("absoluten Kernpunkt", как называл их Планк). Относительно фундаментального статуса этих двух постоянных уже давно сложилось единое мнение, основанное на роли этих постоянных, соответственно, в специальной теории относительности и квантовой механике. Правда, время от времени высказываются сомнения в их фундаментальном статусе даже со стороны выдающихся физиков (например, П.A.M.. Дирак в 1963 г. предположил фундаментальность элементарного заряда е и нефундаментальность постоянной Планка h. Ныне распространились гипотезы об изменении скорости света в вакууме с в связи с предполагаемым изменением постоянной тонкой структуры с космологическим временем), однако все такого рода заключения, как показывает анализ, поспешны, так как основываются на тех или иных ошибочных предпосылках. Этих двух постоянных с и h недостаточно для эталонирования единиц физических величин. Даже для полного эталонирования единиц механических величин наряду с постоянными с и h необходима как минимум еще одна постоянная, не являющаяся их комбинацией. Однако относительно статуса других постоянных пока не существует единого мнения. Наиболее популярно добавление к этим двум постоянным гравитационной постоянной G в силу того, что она фигурирует в основном уравнении общей теории относительности. Однако другие ученые полагают, что G должна редуцироваться к другим более фундаментальным постоянным, а третьи — что она должна меняться с космологическим временем. Еще одна постоянная (пока неоткрытая или известная, но чей статус еще недостаточно оценен) вместе с постоянными с и h позволит эталонировать все единицы механики. Распространено представление, что необходимо и достаточно трех основных единиц для эталонирования всех физических величин. На самом деле это так только для механики, а для эталонирования электромагнитных, гравитационных и термодинамических величин необходимо выбирать или три дополнительные основные единицы или коэффициенты (т. е. три размерные постоянные) в законах равными точно 1 или каким-либо математическим постоянным. Отметим, что все физические законы, в которых проявляется механическое действие тяготения, электромагнетизма или термодинамики, экспериментально устанавливаются в виде пропорциональностей, но не равенств, а коэффициент пропорциональности можно выбирать произвольно. Например, закон Кулона устанавливается как пропорциональность Таким образом, для полного эталонирования единиц всех физических величин, включая механику, теорию тяготения, термодинамику, электродинамику и остальные взаимодействия, необходимо и достаточно выбора пяти постоянных или в качестве единиц измерения или равными точно каким-либо математическим постоянным в тех законах, в которых проявляется механическое действие электромагнетизма или тепла. Это касается всех используемых систем единиц: все они основаны на пяти конвенциональных элементах, связанных с выбором единиц измерения. Например, выбор в качестве основных единиц сантиметра, грамма и секунды вовсе не определяет однозначно ни единиц термодинамических, ни электродинамических величин. И гауссова система, и система Лоренца-Хевисайда это обе системы СГС (сантиметр-грамм-секунда), но они различаются выбором единицы электрического заряда, и, следовательно, всех остальных электромагнитных величин. Чтобы выбрать единицы электромагнитных величин, мы должны либо выбрать в качестве еще одной основной единицы некоторую характерную электромагнитную величину, либо коэффициент в законе Кулона или Ампера (т. е. в законах, в которых проявляется механическое действие электричества) равным точно какому-либо числу, например, 1 (гауссова система) или 1/(4π) (система Лоренца-Хевисайда). Таким образом, во всех существующих системах единиц выполняется следующее равенство: п + т = 5, где п — число основных единиц измерения, a m — количество коэффициентов в законах, выбранных равными точно 1 или той или иной математической постоянной. Поэтому число основных единиц и, следовательно, число фундаментальных размерных постоянных не превышает пяти. Однако физические постоянные дают нам критерий точного числа основных единиц измерений и числа фундаментальных постоянных. В самом деле, почему считается, что для эталонирования единиц механики и теории тяготения необходимо и достаточно трех основных единиц? Предположим, что мы будем использовать только две основные единицы — длину и время, а массу и все остальные динамические величины измерять в кинематических единицах. Очевидно, что при этом кинематическая единица массы может определяться, например, из закона всемирного тяготения, как масса, которая создает на единичном расстоянии единичное ускорение. Однако возможны и равноценны и другие определения массы, например, как масса, гравитационный радиус которой равен единице длины и т. п. Если опираться не на массу, а на плотность, это даст другой спектр определений кинематических единиц динамических величин. Все эти определения будут приводить к тому, что кинематическая размерность массы будет равна L 3/ Т 2, а единица ее измерения — 1 см 3/ с 2, однако при этом величине 1 см 3/ с 2 могут сопоставляться самые различные количества массы, в зависимости от принятых ее кинематических определений. Таким образом, выражение, допустим, 100 см 3/ с 2 ни в коей мере не фиксирует однозначно какое-либо количество массы, пока дополнительно не указано, какой способ определения массы выбран. Поэтому это приводит и к неоднозначности значений физических постоянных. Например, постоянная Планка, выраженная в кинематических единицах, будет иметь произвольное значение: h = произвольное число ´ см 5/ с 3, различающееся при разных кинематических определениях массы для одних и тех же единиц длины и времени. Однако все динамические постоянные приобретают однозначное значение при выборе еще одной, третьей основной единицы (например, единицы массы или силы). Аналогичная ситуация и при определении единиц электромагнитных величин. Если опираться только на три механические единицы (например, сантиметр, грамм и секунда), то это само по себе не определяет однозначно единицы электромагнитных величин. Например, единицу электрического заряда можно выбрать из закона Кулона как величину, которая на единичном расстоянии создает единичное ускорение. Другие определения возможны через закон Ампера или закон Фарадея. Все они будут приводить к разным количествам электрического заряда, которые сопоставляются соответствующей комбинации механических единиц, и, следовательно, к различным значениям электромагнитных физических постоянных в механических единицах. Например, в гауссовой системе единиц (коэффициент в законе Кулона ке выбирается равным точно 1) элементарный электрический заряд е = 4,80320440(15)·10-10 г 1/2 см 3/2 с -1, а в системе Лоренца-Хевисайда (коэффициент в законе Кулона ке выбирается равным 1/(4π), исходя из требования симметрии — так называемая рационализация единиц) тот же самый элементарный заряд е в Таким образом, простое требование однозначности численных значений физических постоянных приводит к необходимости выбора пяти основных единиц измерения, и, следовательно, к пяти размерным фундаментальным постоянным физики. Какие же постоянные следует относить к их числу? В силу вышеуказанной классификации постоянных, основанной на различии в их принципах обоснования, и соответствия между числом фундаментальных постоянных и числом основных единиц мы должны ориентироваться прежде всего на те постоянные, которые являются естественными единицами каких-либо физических величин. Поэтому уточним данное выше определение фундаментальных постоянных: фундаментальные постоянные это метрологически независимые постоянные, являющиеся естественными единицами физических величин, число которых необходимо и достаточно для эталонирования единиц всех физических величин и однозначной фиксации численных значений всех остальных физических констант. С этой точки зрения фундаментальными постоянными являются постоянные с и Например, метрологи не только никогда не утверждали невозможность систем единиц, основанных на постоянных с, h и е, но даже неоднократно предлагали такого рода системы единиц. Более того, открытия квантов магнитного потока, сопротивления и проводимости, являющихся комбинациями постоянных с, h и е (с точностью до множителей типа π или 2π), как раз свидетельствует в пользу фундаментальности всех трех постоянных с, h и е. Однако, очевидно, что этих четырех постоянных недостаточно для полного эталонирования физических величин, т. е. должна существовать еще одна фундаментальная постоянная, являющаяся естественной единицей какой-либо физической величины и метрологически независимая от постоянных с, h, e и k. В частности, одна из размерных констант взаимодействия может оказаться той самой недостающей для полного набора фундаментальной постоянной. В первую очередь это касается гравитационной постоянной G, учитывая роль планковских величин как границ применимости современных теорий. Отметим, что все эти пять постоянных (с, G, h, e, k) являются метрологически независимыми и их выбор достаточен для эталонирования единиц всех физических величин, т. е. они удовлетворяют критерию постоянных С-класса. Однако, не будет большой неожиданностью, если в будущем постоянная G уступит свое место в ряду фундаментальных постоянных какой-либо другой постоянной, являющейся естественной единицей какой-либо физической величины и метрологически независимой от четырех остальных постоянных (например, постоянной Ферми, определяющей через вакуумное среднее h массы частиц, или постоянной L, являющейся естественной единицей энергии в квантовой хромодинамике). В этом случае гравитационная постоянная будет относиться к классу В и выражаться в виде произведения некоторой безразмерной постоянной и комбинации фундаментальных постоянных (т.е. постоянных класса С).
|
||
|
Последнее изменение этой страницы: 2016-09-20; просмотров: 556; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.009 с.) |

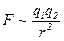 , это же касается принципа эквивалентности, который часто ошибочно трактуется как устанавливающий равенство инертной и гравитационной масс. На самом деле, все опыты типа опытов Этвеша утверждают лишь универсальность коэффициента пропорциональности между инертной и гравитационной массами, и он выбирается равным 1 для простоты, хотя иногда некоторыми учеными формально вводится коэффициент между ними, исходя из тех или иных соображений. Далее мы будем следовать общепринятому выбору равенства инертной и гравитационной масс, а также общепринятому выбору единиц величин слабого и сильного взаимодействий, т. е. полагать достаточным для их описания трех единиц механики, хотя дальнейшее развитие физики может привести и к изменению такого подхода, т. е. к появлению новых размерных постоянных.
, это же касается принципа эквивалентности, который часто ошибочно трактуется как устанавливающий равенство инертной и гравитационной масс. На самом деле, все опыты типа опытов Этвеша утверждают лишь универсальность коэффициента пропорциональности между инертной и гравитационной массами, и он выбирается равным 1 для простоты, хотя иногда некоторыми учеными формально вводится коэффициент между ними, исходя из тех или иных соображений. Далее мы будем следовать общепринятому выбору равенства инертной и гравитационной масс, а также общепринятому выбору единиц величин слабого и сильного взаимодействий, т. е. полагать достаточным для их описания трех единиц механики, хотя дальнейшее развитие физики может привести и к изменению такого подхода, т. е. к появлению новых размерных постоянных. раз больше, чем в гауссовой системе: е = 1,70269163(15)·10-9 г 1/2 см 3/2 с -1, при том, что единицы длины, массы и времени в этих системах совпадают (сантиметр, грамм, секунда) Таким образом, значения элементарного заряда и других электромагнитных постоянных в механических единицах не имеют однозначных значений и им в принципе при желании можно приписать любые численные значения: е = произвольное число ´ 9 г 1/2 см 3/2 с -1. Именно поэтому вместо механических размерностей при постоянных указывается способ выбора единиц, например, "электростатических единиц (esu)". Однако, все электромагнитные постоянные (в том числе, элементарный заряд е) приобретают однозначное значение при выборе еще одной, четвертой основной единицы (например, единицы заряда или тока). Аналогичное требование однозначности численных значений физических постоянных приводит к необходимости выбора пятой основной единицы в термодинамике.
раз больше, чем в гауссовой системе: е = 1,70269163(15)·10-9 г 1/2 см 3/2 с -1, при том, что единицы длины, массы и времени в этих системах совпадают (сантиметр, грамм, секунда) Таким образом, значения элементарного заряда и других электромагнитных постоянных в механических единицах не имеют однозначных значений и им в принципе при желании можно приписать любые численные значения: е = произвольное число ´ 9 г 1/2 см 3/2 с -1. Именно поэтому вместо механических размерностей при постоянных указывается способ выбора единиц, например, "электростатических единиц (esu)". Однако, все электромагнитные постоянные (в том числе, элементарный заряд е) приобретают однозначное значение при выборе еще одной, четвертой основной единицы (например, единицы заряда или тока). Аналогичное требование однозначности численных значений физических постоянных приводит к необходимости выбора пятой основной единицы в термодинамике. , но не гравитационная постоянная G, поскольку она не является естественной единицей никакой физической величины. Однако такие постоянные, как элементарный заряд е, естественная единица электрического заряда, а также постоянная Больцмана k, естественная единица энтропии и теплоемкости, вполне имеют шансы претендовать на роль фундаментальных постоянных. Отметим, что добавление этих двух постоянных к числу фундаментальных не нарушает метрологическую независимость набора с, h, e, k.
, но не гравитационная постоянная G, поскольку она не является естественной единицей никакой физической величины. Однако такие постоянные, как элементарный заряд е, естественная единица электрического заряда, а также постоянная Больцмана k, естественная единица энтропии и теплоемкости, вполне имеют шансы претендовать на роль фундаментальных постоянных. Отметим, что добавление этих двух постоянных к числу фундаментальных не нарушает метрологическую независимость набора с, h, e, k.


