
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Устройство и основные геометрические и силовые соотношенияСодержание книги
Поиск на нашем сайте Зубчатую передачу с пересекающимися осями, у которой начальные и делительные поверхности колес конические, называют конической. Коническая передача состоит из двух конических зубчатых колес и служит для передачи вращающего момента между валами с пересекающимися осями под углом 90°, но могут быть передачи и с ≥≤90°. Колеса конических передач выполняют с прямыми, косыми, круговыми зубьями. Передачу с коническими колесами для передачи вращающего момента между валами со скрещивающимися осями называют гипоидной. Эта передача находит применение в автомобилях.
АОВ — делительный конус шестерни; ВОС - делительный конус колеса; А01В -делительный дополнительный конус шестерни; ВО2С - делительный дополнительный конус колеса; δ1 -угол делительного конуса шестерни; δ2-угол делительного конуса колеса; де1 —внешний делительный диаметр шестерни; де 2 — то же, колеса; д1 —средний делительный диаметр шестерни; д 2 —то же, колеса; в — ширина зубчатого венца (длина зуба); Rе — внешнее делительное конусное расстояние (или длина дистанции). Передаточное число конической передачи определяется так:
i = ω1 /ω2 = п1/ п2 = де 2/ де 1 = z2/z1 = 1/tgδ1 = tgδ2 В конической передаче может быть бесчисленное множество делительных окружностей. Для расчета в машиностроении принимают только внешнюю и среднюю делительные окружности. Из условия, что в конической передаче модуль и делительный диаметр связаны теми же соотношениями, что и в цилиндрических передачах, т. е. d = тz определяют внешний dе и средний d делительные диаметры: de = тez d = тz где те — внешний окружной модуль; m — средний окружной модуль. Внешний окружной модуль обычно выбирают из стандартного ряда. Округление внешнего модуля до стандартного значения не является обязательным требованием. Этот модуль называют производственным и по его значению определяют все геометрические параметры зубчатых колес (задают размеры зубьев на внешнем торце, на котором удобно производить измерения). Средний окружной модуль т рассчитывают в зависимости от внешнего окружного модуля т е. По среднему окружному модулю производят расчет передачи на прочность при изгибе. Стандартизован внешний делительный диаметр конического колеса, а модуль может быть нестандартны § 9. Зубчатые передачи с зацеплением Новикова. Устройство, основные геометрические соотношения
Передачи с зацеплением Новикова состоят из двух цилиндрических косозубых колес или конических колес с винтовыми зубьями и служат для передачи момента между валами с параллельными или пересекающимися осями.
Обычно профиль зубьев шестерни делается выпуклым, а профиль зубьев колес вогнутым или наоборот, но могут быть передачи и с профилем зубьев шестерни и колеса смешанной формы. Такая конструкция зубьев увеличивает нагрузочную способность данной передачи по сравнению с эвольвентной передачей при равных условиях. В зацеплении Новикова контакт зубьев теоретически осуществляется в точке, в эвольвентном зацеплении соприкосновение зубьев происходит по линии. Однако при одинаковых габаритных размерах передачи соприкосновение зубьев в зацеплении Новикова значительно лучше, чем соприкосновение в эвольвентном зацеплении.
Недостатками являются большая (чем в эвольвентных зацеплениях) чувствительность к изменению межосевого расстояния; с увеличением нагрузки в зацеплении возрастает осевая составляющая, что, в свою очередь, усложняет конструкцию применяемых подшипниковых узлов; при ухудшении контакта (например, в случае перекоса валов и изменения межосевого расстояния) вся нагрузка, действующая на зубья, может сосредоточиться па небольшом участке длины зубьев, в результате чего зубья могут оказаться сильно перегруженными; необходимость иметь Две специальные фрезы для нарезания зубьев (для шестерни и колеса).
Планетарные зубчатые передачи.
|
||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 839; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

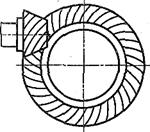
 По стоимости конические передачи дороже цилиндрических при равных силовых параметрах. Их применение диктуется только необходимостью передавать момент при пересекающихся осях валов. Передаточное число одной пары и ≤6,3.
По стоимости конические передачи дороже цилиндрических при равных силовых параметрах. Их применение диктуется только необходимостью передавать момент при пересекающихся осях валов. Передаточное число одной пары и ≤6,3.
 Вершины начальных и делительных конусов конической передачи находятся в точке пересечения осей валов О. Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи:
Вершины начальных и делительных конусов конической передачи находятся в точке пересечения осей валов О. Высота и толщина зубьев уменьшаются по направлению к вершинам конусов. Геометрические параметры конической передачи:


 Особенность зацепления Новикова состоит в том, что в этом зацеплении первоначальный линейный контакт заменен точечным, превращающимся под нагрузкой в контакт с хорошим прилеганием. Простейшими профилями зубьев, обеспечивающими такой контакт, являются профили, очерченные по дуге окружности или близкой к ней кривой.
Особенность зацепления Новикова состоит в том, что в этом зацеплении первоначальный линейный контакт заменен точечным, превращающимся под нагрузкой в контакт с хорошим прилеганием. Простейшими профилями зубьев, обеспечивающими такой контакт, являются профили, очерченные по дуге окружности или близкой к ней кривой. Достоинства и недостатки передач с зацеплением Новикова. Высокая нагрузочная способность является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше допускаемой нагрузки для эвольвентных прямозубых передач тех же основных размеров, выполненных из тех же материалов, с той же термической обработкой (сравнение допускаемых нагрузок произведено при коэффициенте нагрузки К = 1). Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны: имеют почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой передаваемой мощности. Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо удерживающейся масляной пленки между соприкасающимися зубьями уменьшается изнашивание зубьев, повышается КПД передачи (потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном зацеплении). Шум во время их работы значительно ниже.
Достоинства и недостатки передач с зацеплением Новикова. Высокая нагрузочная способность является основным достоинством передач с зацеплением Новикова. При твердости рабочих поверхностей до НВ 350 можно принимать допускаемую нагрузку примерно в 2,5 раза больше допускаемой нагрузки для эвольвентных прямозубых передач тех же основных размеров, выполненных из тех же материалов, с той же термической обработкой (сравнение допускаемых нагрузок произведено при коэффициенте нагрузки К = 1). Благодаря большей нагрузочной способности передачи с зацеплением Новикова более компактны: имеют почти в 2 раза меньшие габариты по сравнению с передачами с эвольвентным зацеплением при одинаковой передаваемой мощности. Передачи с зацеплением Новикова допускают большее передаточное число, а вследствие хорошо удерживающейся масляной пленки между соприкасающимися зубьями уменьшается изнашивание зубьев, повышается КПД передачи (потери на трение в зацеплении Новикова примерно в 2 раза меньше, чем потери в эвольвентном зацеплении). Шум во время их работы значительно ниже.



