Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Запись результатов измерений.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Проводя расчеты при обработке результатов измерений, в особенности с использованием вычислительной техники, мы получаем результат, как правило, с большим количеством значащих цифр. Очевидно, что высокая точность вычислений не может сама по себе привести к увеличению точности результата измерений. Например, погрешность измерения скорости тела равна · Результат измерений и расчетов не должен записываться с большим числом десятичных знаков, чем их имеется в абсолютной погрешности. · Абсолютная погрешность округляется до одной значащей цифры (или до двух, если первая цифра оказалась единицей). · Полученный результат лучше записывать в стандартной форме, т.е. в виде произведения числа, лежащего между единицей и десятью, и числа, представляющего собой степень десяти. Например, число 365 можно записать в виде 3,65·102. В таблице 3 приведены примеры верной и неверной записи результатов. Таблица3. Примеры верной и неверной записи результатов измерений
Прогресс физики и других разделов естествознания во многом определяется точностью экспериментов. В настоящее время достигнута поразительная точность при измерении ряда физических величин (расстояние, время и др.). Так, с помощью молекулярных генераторов и стандартов частоты удается осуществить такие молекулярные часы, что их ошибка составляет всего одну секунду за 106 лет, т.е. относительная погрешность равна 10-12%. С очень высокой точностью измерена и такая важнейшая физическая величина как скорость распространения света в вакууме с=(299792458,0 ± 1,2)м/с. При обычных измерениях, например в физическом практикуме, конечно, не удается достичь таких прецизионных точностей измерений, которые во многом определяются погрешностью используемых приборов. Вместе с тем при работе в практикуме нужно стремиться к уменьшению ошибок измерения, правильно производить их оценки и грамотно оформлять промежуточные и окончательные результаты измерений.
КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Расскажите о прямых и косвенных измерениях. 2. Что такое чувствительность приборов и пределы измерений? 3. Что такое цена делений? Как определить цену делений шкалы? 4. Абсолютная и относительные погрешности. Их смысл и значение. 5. Расскажите о систематических погрешностях. 6. Как оцениваются погрешности приборов? 7. Расскажите о случайных ошибках. Как их можно уменьшить? 8. Расскажите о среднем значении измеряемой величины и о средней квадратичной погрешности отдельного измерения. 9. Как находится полная погрешность измерения? 10. Расскажите о порядке обработки результатов прямых измерений. 11. Как определяются наилучшее значение и погрешность при косвенных измерениях? 12. Расчетная формула имеет вид x = A B / (C + D), где A, B, C – независимо измеренные величины. Как подсчитать погрешность косвенного измерения величины x? Укажите различные алгоритмы вычислений. 13. Какова погрешность табличных данных? 14. Как следует округлять результаты измерений? 15. Как рассчитать масштаб при построении графиков? 16. Расскажите о методе натянутой нити. 17. Расскажите о методе наименьших квадратов. Лабораторная работа №1 ОПРЕДЕЛЕНИЕ ПЛОТНОСТИ ОДНОРОДНОГО ТВЁРДОГО ТЕЛА ПРАВИЛЬНОЙ ГЕОМЕТРИЧЕСКОЙ ФОРМЫ. Цели работы: 1. Изучить устройство штангенциркуля и научиться измерять линейные размеры тела с его помощью. 2. Изучить устройство микрометра и научиться измерять линейные размеры тела с его помощью. 3. Изучить правила пользования весами и научиться измерять массу тел с помощью технических или электронных весов ВЛТЭ-1100. Приборы и принадлежности: электронные или технические весы с разновесом, штангенциркуль, микрометр, однородное твёрдое тело. ТЕОРЕТИЧЕСКОЕ ВВЕДЕНИЕ. Плотностью однородного тела называется физическая величина численно равная массе, заключённой в единице объёма этого тела. Плотность однородного тела вычисляется по формуле:
где а) ИЗМЕРЕНИЕ МАССЫ. Измерение массы на технических весах.
В работе с техническими весами следует руководствоваться следующими обязательными правилами (см. паспорт к весам): 1. При помощи регулируемых ножек установить весы по имеющемуся на них отвесу. 2. Освободить коромысло весов с ненагруженными чашками и убедиться в том, что оно свободно качается, причём стрелка-указатель колеблется около нулевого деления шкалы (равновесие регулируется винтами, расположенными на обоих концах коромысла). В нерабочем состоянии коромысло весов фиксируется (арретируется) в таком положении при котором опорные призмы оказываются не нагруженными. Фиксация и освобождение коромысла производится при помощи специального приспособления называемого арретиром. Арретир включается и выключается поворотом рукоятки, расположенной на передней стороне основания весов. 3. Любое изменение нагрузки весов производится только тогда, когда весы арретированы (зафиксированы). 4. Взвешиваемое тело и гири помещать на середину чашек весов. 5. Брать гири и ставить их назад в гнёзда ящика разновеса только пинцетом. Для больших гирь можно использовать специальную салфетку. Измерение массы на электронных весах: 1. При помощи регулируемых ножек установить весы горизонтально по имеющемуся на них уровню. 2. Включить весы и дать им немного прогреться. В ненагруженном состоянии показания весов должны быть нулевые. 3. Поставить груз в центр чашки весов и записать показания. Задания: 1. Измерьте массу тела с помощью электронных или технических весов и запишите результат в таблицу. Провести все необходимые прямые изменения с надёжностью не ниже ρ= 0,90. 2. Оцените погрешность измерения массы на весах с помощью паспорта прибора и набора гирь (для технических весов). Запишите ее в таблицу. 3. Найдите относительную погрешность измерения массы по формуле em= Dm/m. и занесите ее в таблицу. б) ИЗМЕРЕНИЕ ШТАНГЕНЦИРКУЛЕМ.
При измерении наружного размера тело помещают между губками 3 и 6. Губки 2 и 5 используются при измерении внутренних размеров, а рейка - при измерении глубин. Вдоль штанги нанесена шкала с миллиметровыми делениями. На скошенном краю рамки, скользящей по штанге, нанесена маленькая вспомогательная шкала, называемая нониусом и предназначенная для увеличения точности измерения в несколько раз. Использование нониуса основано на том, что факт совпадения двух штрихов или несовпадения наш глаз фиксирует хорошо. Оценить же расстояние между двумя штрихами гораздо сложнее. Ширина делений на нониусе делается на 0,1 (0,05) короче, чем ширина делений основной шкалы.
Рассмотрим случай, когда начало нониуса совпадает с одним из делений основной шкалы (рис.6). Тогда первое деление нониуса отстаёт от ближайшего деления шкалы справа на 0,1 мм, второе на 0,2 мм,..., седьмое на 0,7 мм и т.д.
При сдвиге нониуса вправо на 0,2 мм, лучше всего с делением основной шкалы совпадёт второе деление, при сдвиге на 0,6 мм совпадает шестое деление нониуса и т.д. Таким образом, в любом положении только одно из делений нониуса совпадёт с одним делением основной шкалы.
Минимальное изменение длины, регистрируемое нониусом, равно его точности d. Поэтому d можно рассматривать как цену деления штангенциркуля. Эта же величина принимается за систематическую погрешность штангенциркуля. Перейдём к измерению с помощью нониуса. На рис. 7 видно, что расстояние, на которое сдвинулось нулевое деление нониуса равно диаметру измеряемого цилиндра. В нашем случае оно 2 мм < Всегда легко определить целое число миллиметров, число же десятых долей определяется на основании совпадения делений нониуса и основной шкалы. Мы рассмотрели простой наглядный случай, когда ширина делений основной шкалы (1мм) отличалась от ширины делений нониуса на 0,1 мм. Возможны нониусы с шириной 1,9 мм; 2,9 мм; 1,95 мм и др. Задания: 1. Изучить устройство штангенциркуля. 2. Определите ширину делений нониуса, основной шкалы. Чему равна ошибка прибора dh? Занесите ее в таблицу. 3. Измерьте с помощь штангенциркуля линейные размеры тела. Результаты занесите в таблицу. Провести все необходимые прямые изменения с надёжностью не ниже ρ = 0,90 4. По формуле (5) вычислите среднее арифметическое измеренных значений и занесите его в таблицу. 5. Найдите случайную ошибку либо по формуле 6. По формуле (8) найдите полную ошибку Dh измерений, а по формуле (2) относительную ошибку. Занесите их в таблицу. в) ИЗМЕРЕНИЕ МИКРОМЕТРОМ.
 Микрометр - это прибор для измерения линейных размеров тел при помощи микрометрического винта. Шаг микрометрического винта с высокой точностью постоянен по всей его длине. Для измерительных целей микрометрический винт соединен с корпусом барабана, при вращении которого, происходит поступательное перемещение микровинта. Причем малое перемещение винта сопровождается поворотом барабана на значительный угол. Если по окружности барабана равномерно нанесено Микрометр - это прибор для измерения линейных размеров тел при помощи микрометрического винта. Шаг микрометрического винта с высокой точностью постоянен по всей его длине. Для измерительных целей микрометрический винт соединен с корпусом барабана, при вращении которого, происходит поступательное перемещение микровинта. Причем малое перемещение винта сопровождается поворотом барабана на значительный угол. Если по окружности барабана равномерно нанесено  делений, то при повороте барабана на одно деление винт смещается на делений, то при повороте барабана на одно деление винт смещается на  мм, где мм, где  - шаг винта в мм. Величина - шаг винта в мм. Величина  называется точностью микрометрического винта. называется точностью микрометрического винта.
Микрометр для измерения наружных размеров (рис.8) состоит из скобы 1 жёстко соединённый с трубкой 2 и подвижного торца микрометрического винта 3 с барабаном 4. На скобе размещены упор 5 и стопор 6. На поверхности трубки вдоль её образующей расположена шкала 7, а внутри проходит микрометрический винт. На скошенном срезе его барабана нанесена круговая шкала 8. Измеряемый предмет зажимают между упором 5 и торцом 3 путём вращения барабана. Вращать барабан следует только за фрикционную головку (трещотку). Непосредственно перед зажимом предмета вращение должно быть медленным. Когда нажим на предмет достигает нормальной величины, трещотка, проскальзывая, издает щелчки. Вращение барабана без использования трещотки может вывести прибор из строя.
Указателем для отсчёта показаний круговой шкалы 8 служит горизонтальная черта, разделяющая линейную шкалу 7. Круговая шкала содержит 50 делений (реже 100). Для удобства отсчёта деления пронумерованы. Микрометры изготовляются так, чтобы погрешность прибора не превышала точности микрометрического винта.
Необходимо быть особенно внимательными, когда показания прибора незначительно отличаются от целого или полуцелого числа миллиметров. В этом случае из-под барабана уже видна метка соответствующего деления. Когда учитывать показавшееся деление, а когда нет? Как правило, метка начинает выступать из-под края барабана тогда, когда на нем около 40 делений. В этом случае мы еще только приближаемся к данному значению, но не достигли его. Учитывать ее надо с того момента, когда показание круговой шкалы достигнет 50 делений. Исходя из этого, можно сформулировать следующее правило учета показавшейся метки: «Выглядывающую» из под барабана метку не учитывают, если на круговой шкале мы находимся в конце шкалы и учитывают, если на круговой шкале менее 20 делений (начало шкалы). Задания: 1. Изучить устройство микрометра и научиться правильно производить отсчёт его показаний. (Нужно чётко различать такие показания как 2,95 мм, 2,45 мм и 3,45 мм, 5,48 мм и 5,98 мм, 4,96 мм и 5,04 мм). 2. Определите ошибку прибора и занести ее в таблицу. 3. Измерьте с помощью микрометра диаметры предмета. (не менее 5 раз каждый). Запишите результаты в таблицу. 4. По данным измерений найдите среднее арифметическое значение. Запишите его в таблицу.
5. Определите случайную и полную квадратичную погрешность измерения величины. 6. Используя средние значения, измеренных величин, найдите плотность материала, из которого изготовлено тело. 7. По таблице 4 плотностей определите, из какого материала изготовлен образец. 8. Используя расчетную формулу и таблицу2 запишите формулу для относительной погрешности измерения плотности er. Покажите ее преподавателю и если она верна проведите расчеты. 9. Найдите абсолютную погрешность измерения плотности по формуле Dr = er×r 10. Запишите полученный результат в стандартной форме. Таблица 4. Таблица плотностей твердых тел
КОНТРОЛЬНЫЕ ВОПРОСЫ. 1. Что такое плотность вещества? В чем ее физический смысл? 2. Что характеризует плотность свойство тела или свойства вещества? 3. Как изменяется плотность тела при изменении температуры? 4. Что называется абсолютной погрешностью? Что является источником систематических и случайных погрешностей? Почему относительная погрешность лучше характеризует качество измерений, чем абсолютная? Примеры. 5. Как пользоваться микрометром, штангенциркулем, весами? 6. Какова погрешность отсчёта при измерении этими приборами? 7. Каковы правила округления результатов вычислений. Привести примеры. 8. Что называется стандартной формой записи приближенного числа? 9. Что означает такая запись: 10. Какие цифры называют верными в приближённом числе, какие сомнительными? 11. Какие ошибки допущены в следующей записи конечного результата измерения объёма: 12. Как узнать есть ли в отливке внутренние пустоты (раковины), если известен материал, из какого она изготовлена?
ЛИТЕРАТУРА: 1. Зайдель А.Н. Ошибки измерения физических величин.- М.: Наука, 1974. 2. Лабораторные занятия по физике./Под ред. А.Д.Гольдина.- М.: Наука, 1983. 3. Лабораторный практикум по общей физике./Под ред. Е.М.Гершензона и Н.М.Малова.- М.: Просвещение, 1985. 4. Методические указания к лабораторным занятиям по физике. Вводные сведения о физических измерениях и обработке результатов.- Смоленск, 1986. 5. Лаврова И.В. Курс физики. - М.: Просвещение, 1981. 6. Енохович А.С. Справочник по физике и технике.- М.: Просвещение 1989.- 224с. 7. Дмитриева В.Ф., Прокофьев В.Л. Основы физики6 Учебное пособие для студентов вузов. – М.: Высшая школа, 2001.- 527с. 8. Никифоров Г.Г. Погрешности измерений при выполнении лабораторных работ по физике. 7-11 кл.- М.: Дрофа, 2004.-112с.: ил. 9. Методические указания к лабораторным занятиям по физике: Механика. Выпуск первый. – Смоленск, 1987. 10. Методические указания к лабораторным занятиям по физике: Механика. Выпуск второй. – Смоленск, 1990.
Приложение
ОГЛАВЛЕНИЕ ПРЕДИСЛОВИЕ (ПАМЯТКА СТУДЕНТУ). - 3 - §1 ФИЗИЧЕСКИЕ ИЗМЕРЕНИЯ. ВИДЫ ИЗМЕРЕНИЙ... - 7 - §2 ПОГРЕШНОСТИ ИЗМЕРЕНИЙ ФИЗИЧЕСКИХ.. - 13 - ВЕЛИЧИН.. - 13 - §3 ПОГРЕШНОСТИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ.. - 16 - §5 ПОРЯДОК ОБРАБОТКИ РЕЗУЛЬТАТОВ ПРЯМЫХ ИЗМЕРЕНИЙ ФИЗИЧЕСКОЙ ВЕЛИЧИНЫ... - 27 - §6 ОБРАБОТКА РЕЗУЛЬТАТОВ КОСВЕННЫХ ИЗМЕРЕНИЙ... - 29 - §7 ПОСТРОЕНИЕ И ИСПОЛЬЗОВАНИЕ ГРАФИКОВ ПРИ ОБРАБОТКЕ РЕЗУЛЬТАТОВ. - 30 - §8 ЗАПИСЬ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ. - 37 - КОНТРОЛЬНЫЕ ВОПРОСЫ... - 39 - Лабораторная работа №1.. - 40 - а) ИЗМЕРЕНИЕ МАССЫ. - 40 - б) ИЗМЕРЕНИЕ ШТАНГЕНЦИРКУЛЕМ. - 42 - в) ИЗМЕРЕНИЕ МИКРОМЕТРОМ. - 44 - КОНТРОЛЬНЫЕ ВОПРОСЫ. - 48 - ЛИТЕРАТУРА: - 49 - Приложение. - 50 - ОГЛАВЛЕНИЕ.. - 52 -
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 3616; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.220.13.15 (0.017 с.) |

 , а вычисление самой скорости с использованием калькулятора дало значение v =0,5603025035 (м/с). Такая запись означает, что скорость измерена с погрешностью 0,0000000005= 5·10-10(м/с), что абсурдно, так как реальная погрешность измерения значительно выше. Для того чтобы не делать таких ошибок все цифры в окончательной записи результата должны быть обоснованными. При этом следует соблюдать следующие правила:
, а вычисление самой скорости с использованием калькулятора дало значение v =0,5603025035 (м/с). Такая запись означает, что скорость измерена с погрешностью 0,0000000005= 5·10-10(м/с), что абсурдно, так как реальная погрешность измерения значительно выше. Для того чтобы не делать таких ошибок все цифры в окончательной записи результата должны быть обоснованными. При этом следует соблюдать следующие правила: 2.
2. 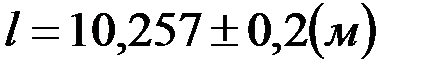 3.
3.  4.
4. 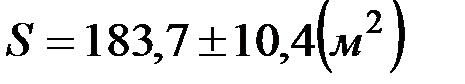
 2.
2. 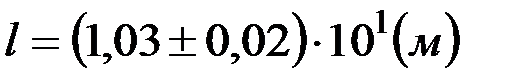 3.
3.  4.
4. 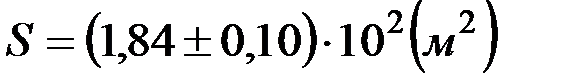
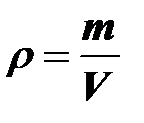 ,
,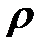 - плотность,
- плотность,  - масса тела,
- масса тела, 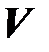 - его объём.
- его объём.
 < 3 мм. Т.к. деления основной шкалы везде одинаковые и совпало 6-е деление нониуса, значит, нониус сдвинут вправо на 0,6 мм от пятого деления основной шкалы. Следовательно
< 3 мм. Т.к. деления основной шкалы везде одинаковые и совпало 6-е деление нониуса, значит, нониус сдвинут вправо на 0,6 мм от пятого деления основной шкалы. Следовательно  .
. , где n число измерений, либо с помощью калькулятора, имеющего функцию статистических расчетов. Запишите ее в таблицу.
, где n число измерений, либо с помощью калькулятора, имеющего функцию статистических расчетов. Запишите ее в таблицу.
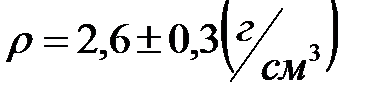 ?
? ?
?




 ,
, 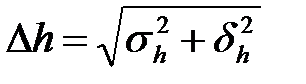 ,
, 
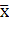
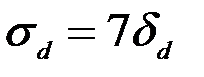 , поэтому
, поэтому  м.
м.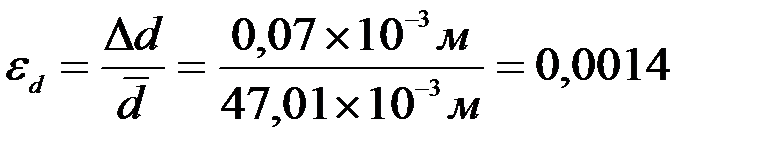

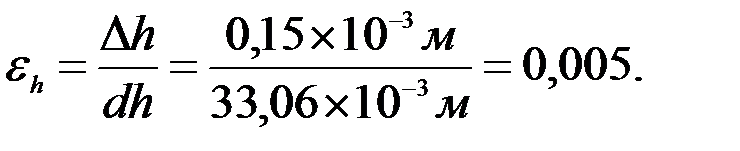

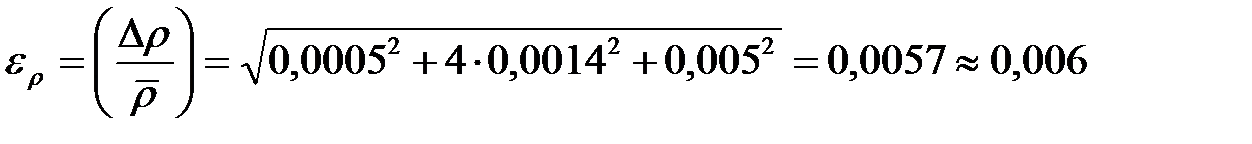

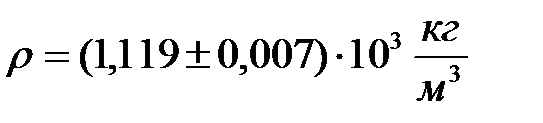 ,
,