
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Потенциальная энергия взаимодействия электрических зарядов: система точечных зарядов; система заряженных проводников; энергия заряженного конденсатора.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
14) Потенциальная энергия заряда в электрическом поле. Работу, совершаемую силами электрического поля при перемещении положительного точечного заряда q из положения 1 в положение 2, представим как изменение потенциальной энергии этого заряда:
где Wп1 и Wп2 – потенциальные энергии заряда q в положениях 1 и 2. При малом перемещении заряда q в поле, создаваемом положительным точечным зарядом Q, изменение потенциальной энергии равно При конечном перемещении заряда q из положения 1 в положение 2, находящиеся на расстояниях r1 и r2 от заряда Q,
Если поле создано системой точечных зарядов Q1, Q2,¼, Qn, то изменение потенциальной энергии заряда q в этом поле:
Приведённые формулы позволяют найти только изменение потенциальной энергии точечного заряда q, а не саму потенциальную энергию. Для определения потенциальной энергии необходимо условиться, в какой точке поля считать ее равной нулю. Для потенциальной энергии точечного заряда q, находящегося в электрическом поле, созданном другим точечным зарядом Q, получим
где C – произвольная постоянная. Пусть потенциальная энергия равна нулю на бесконечно большом расстоянии от заряда Q (при r ® ¥), тогда постоянная C = 0 и предыдущее выражение принимает вид При этом потенциальная энергия определяется как работа перемещения заряда силами поля из данной точки в бесконечно удаленную. В случае электрического поля, создаваемого системой точечных зарядов, потенциальная энергия заряда q:
Потенциальная энергия системы точечных зарядов. В случае электростатического поля потенциальная энергия служит мерой взаимодействия зарядов. Пусть в пространстве существует система точечных зарядов Qi (i = 1, 2,..., n). Энергия взаимодействия всех n зарядов определится соотношением
где r i j - расстояние между соответствующими зарядами, а суммирование производится таким образом, чтобы взаимодействие между каждой парой зарядов учитывалось один раз. Магнитные взаимодействия: опыты Эрстеда и Ампера; магнитное поле; сила Лоренца, индукция магнитного поля; силовые линии магнитного поля; магнитное поле, создаваемое движущимся с постоянной скоростью точечным зарядом. Магнитное поле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1], магнитная составляющая электромагнитного поля[2] Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты). Опыт Эрстеда показал, что электрические токи могут действовать на магниты, однако природа магнита в то время была совершенно таинственной. Ампер и другие вскоре открыли взаимодействие электрических токов друг с другом, проявляющееся, в частности, как притяжение между двумя параллельными проводами, по которым текут одинаково направленные токи. Это привело Ампера к гипотезе, что в магнитном веществе имеются постоянно циркулирующие электрические токи. Если такая гипотеза справедлива, то результат опыта Эрстеда можно объяснить взаимодействием гальванического тока в проволоке с микроскопическими токами, которые сообщают стрелке компаса особые свойства Сила Лоренца — сила, с которой, в рамках классической физики, электромагнитное поледействует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью
Для непрерывного распределения заряда, сила Лоренца принимает вид:
где d F — сила, действующая на маленький элемент dq. ИНДУКЦИЯ МАГНИТНОГО ПОЛЯ Более конкретно,
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора Действие магнитных полей на электрические токи: закон Био-Савара-Лапласа-Ампера и его применение для расчета силы, действующей со стороны однородного магнитного поля на отрезок тонкого прямого проводника с током; формула Ампера и ее значение в метрологии. Рассмотрим произвольный проводник,в котором протекают токи: dF= З-н Био-Савара-Ампера для объемного тока:dF=jBdVsin Задача 1! Имеется однородное магнитное поле. В нем нах-я отрезок провода,который имеет l и I. d 1 Ампер-сила тока,при протекании которого по 2 || длинным,тонким проводникам,находящимся на расстоянии 1 м друг от друга действует сила равная 2*10^-7 Н на каждый метр их длины. Задача 2! Есть 2 || длинных проводника, где l >>d,тогда d Магнитный диполь: физическая модель и магнитный момент диполя; магнитное поле, создаваемое магнитным диполем; силы, действующие со стороны однородного и неоднородного магнитных полей на магнитный диполь. ДИПОЛЬ МАГНИТНЫЙ аналог диполя электрического, к-рый можно представлять себе как два точечных магн. заряда Поля, создаваемые равными Д. м. 38. Теорема Гаусса для магнитного поля: интегральная и дифференциальная формы, физический смысл теоремы. Релятивистский характер магнитного поля: магнитные взаимодействия как релятивистское следствие электрических взаимодействий; взаимные преобразования электрических и магнитных полей.
Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора В не имеют ни начала, ни конца. Поток вектора В через замкнутую поверхность должен быть равен нулю. Таким образом, для любого магнитного поля и произвольной замкнутой поверхности S имеет место условие Эта формула выражает теорему Гаусса для вектора В: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю. В интегральной форме 1. Поток вектора электрического смещения через любую замкнутую поверхность, окружающую некоторый объем, равен алгебраической сумме свободных зарядов, находящихся внутри этой поверхности В дифференциальной форме Пусть в объеме
где
При стягивании объема в точку
39. Теорема о циркуляции вектора магнитной индукции стационарного магнитного поля для вакуума: интегральная и дифференциальная формы, физический смысл теоремы; применение теоремы для расчета магнитных полей на примере магнитного поля, создаваемого бесконечно длинным соленоидом с током. Теорема. Циркуляция вектора магнитной индукции В по замкнутому контуру L равна алгебраической сумме токов, охватываемых данным контуром L, умноженной на μ0. Примеры:
I3 I1 I2
Применяя принцип суперпозиции к магнитным полям, получаем:
Если токи протекают в сплошной среде, получаем: Теорема Стокса:
|
||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 530; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.12.73.221 (0.008 с.) |



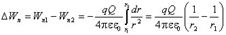





 заряд
заряд  лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического
лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще[1], иначе говоря, со стороны электрического  и магнитного
и магнитного  полей. Выражается в СИ как:
полей. Выражается в СИ как:

 — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой
— векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой 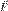 магнитное поле действует на заряд
магнитное поле действует на заряд 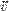 .
. — это такой вектор, что сила Лоренца
— это такой вектор, что сила Лоренца  , действующая со стороны магнитного поля[1] на заряд
, действующая со стороны магнитного поля[1] на заряд  , равна
, равна

 перпендикулярно им обоим и направлено поправилу буравчика).
перпендикулярно им обоим и направлено поправилу буравчика). []*ndV=[
[]*ndV=[  ]*dV
]*dV . dF перпендикулярно
. dF перпендикулярно  ,т.е. направленно к нам. Возьмем тонкий проводник:
,т.е. направленно к нам. Возьмем тонкий проводник:  , тогда для линейного эл-а тока з-н запишется в виде: dF=I [
, тогда для линейного эл-а тока з-н запишется в виде: dF=I [  ], т.е. dF=IBdlsin
], т.е. dF=IBdlsin  .
. =I [
=I [  =IBlsin
=IBlsin  =
=  , d
, d  d
d  ,
, 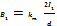 . Тогда ф-а Ампера:
. Тогда ф-а Ампера:  * l.
* l. , расположенных на расстоянии l друг от друга. Характеризуется дипольным моментом, равным по величине
, расположенных на расстоянии l друг от друга. Характеризуется дипольным моментом, равным по величине  и направленным от
и направленным от  .
. вне области источников в вакууме (или в любой иной среде, магн. проницаемость к-рой
вне области источников в вакууме (или в любой иной среде, магн. проницаемость к-рой  =1), одинаковы, однако в средах с
=1), одинаковы, однако в средах с  совпадение достигается, если только принять, что
совпадение достигается, если только принять, что  , т. е. считать, что дипольный момент зарядового Д. м. зависит от проницаемости
, т. е. считать, что дипольный момент зарядового Д. м. зависит от проницаемости

 Вектор
Вектор  – это такая характеристика поля, которая не зависит от диэлектрических свойств среды.
– это такая характеристика поля, которая не зависит от диэлектрических свойств среды. имеется
имеется ,
, - средняя по объему плотность. Тогда
- средняя по объему плотность. Тогда .
. .
. - теорема Гаусса в дифференциальной форме
- теорема Гаусса в дифференциальной форме

 ,
, 
 – ток за пределами контура.
– ток за пределами контура.

 где S-поверхность ограниченная контуром L.
где S-поверхность ограниченная контуром L. - теорема о циркуляции вектора магнитной индукции.
- теорема о циркуляции вектора магнитной индукции.


