
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Объемная плотность энергии магнитного поля. Механические силы в стационарном магнитном поле: метод виртуальных перемещений; давление магнитных сил.Содержание книги
Поиск на нашем сайте
Плотность энергии магнитного поля – количество магнитной энергии в единице объема соленоида: Где H=In Итак: Аналогично Механические силы в стационарном магнитном поле
где Fx - сила, действующая на цепь в направлении х Вследствие перемещения цепи произойдет изменение магнитного поля системы:.
В соответствии с законом сохранения энергии составим баланс энергий:, или Составляющие силы, действующей на электрическую цепь в направлении осей координат x, y, z: . Результирующая сила направлена в сторону наибольшего возрастания энергии магнитного поля. Так как по условию токи цепей постоянны, то и энергия собственного магнитного поля, равная тоже постоянна, а изменяется только взаимная энергия системы Wвз и, следовательно, сила. Если система состоит только из двух магнитносвязанных цепей, то энергия магнитного поля будет равна: . Тогда получим: В измерительных приборах электродинамической системы вращающий момент, действующий на подвижную систему прибора, будет равен: , т.е. вращающий момент пропорционален скорости изменения взаимной индуктивности М при повороте подвижной системы прибора. Переходные процессы в цепи с постоянной ЭДС и индуктивностью: временные зависимости токов и напряжений при нарастании и спаде тока в катушке индуктивности; постоянная времени электрической цепи с индуктивностью.
Установившийся ток в этой цепи будет определяться только ЭДС E и резистивным сопротивлением R, т.к. после окончания переходного процесса i = const и uL = Ldi / dt = 0, т.е. i у = E / R. Полный ток в переходном процессе из выражения (1)
Для определения постоянной I найдем начальное тока. До замыкания ключа ток очевидно был нулевым, а т.к. подключаемая цепь содержит индуктивность, ток в которой не может измениться скачкообразно, то в первый момент после коммутации ток останется нулевым. Отсюда
Подставляя найденное значение постоянной I в выражение для тока, получим
Из этого выражения можно определить падения напряжения на резисторе uR и индуктивности uL
Из выражений (1)-(3) следует, что ток в цепи нарастает по экспоненте с постоянной времени = L / R от нулевого до значения E / R (рис. 1 б)). Падение напряжения на сопротивлении uR повторяет кривую тока в измененном масштабе. Напряжение на индуктивности uL в момент коммутации скачкообразно возрастает от нуля до E, а затем снижается до нуля по экспоненте (рис. 1 б)). Подставляя выражения (3) в уравнение Кирхгофа для цепи после коммутации, можно убедиться в его справедливости в любой момент времени
Свободные незатухающие электромагнитные колебания в параллельном контуре: взаимные превращения энергии электрических и магнитных полей; уравнение незатухающих колебаний, период собственных незатухающих колебаний в контуре. Колебательный контур-это электрическая цепь, состоящая из емкости С и катушки индуктивности L, в которой обкладки конденсатора замкнуты катушкой индуктивности. Дифференциально е уравнение свободных незатухающих колебаний имеет вид:
где Решением дифференциального уравнения (1) является функция Где
С учетом определения силы тока, функция зависимости силы тока в катушке будет иметь вид:
Т.о, при свободных незатухающих колебаниях ток в катушке опережает по фазе напряжение на конденсаторе на Cучетом выражения Свободные затухающие электромагнитные колебания в параллельном контуре: коэффициент затухания и добротность контура; уравнение затухающих колебаний; период собственных затухающих колебаний в контуре, критическое затухание. Колебательный контур-это электрическая цепь, состоящая из емкости С и катушки индуктивности L, в которой обкладки конденсатора замкнуты катушкой индуктивности. Каждый реальный контур обладает активным сопротивлением, и энергия, запасенная в контуре, постепенно расходуется на нагревание проводов. При таких условиях свободные электромагнитные колебания будут затухающими. Дифференциальное уравнение затухающих свободных колебаний имеет вид:
Где ω Величину Время релаксации τ-время, за которое амплитуда колебаний уменьшается в e раз. Коэффициент затухания β связан с временем релаксации соотношением:
Логарифмический декремент затухания λ определяется как натуральный логарифм отношения двух значений амплитуд, взятых через интервал времени, равный периоду колебаний T:
Где α- амплитуда соответствующей физической величины(q,U,I) Если
Добротность колебательного контура характерезует“эффективность” рассеяния энергии контура при наличии в нем активного сопротивления. Эта величина определяется из оcотношения:
Вынужденные колебания-незатухающие колебания, возникающие в R,L,C – цепи под действием внешнего периодически изменяющегося напряжения:
Где Активное сопротивление, емкость и индуктивность в цепи синусоидального переменного тока: временные зависимости мгновенных значений сил тока, напряжений и мощностей; активные и реактивных сопротивления, сдвиги фаз, активные мощности. Сопротивление: Если напряжение
Анализ выражения (1) показывает, что напряжение на сопротивлении и ток, протекающий через него, совпадают по фазе.
где Из анализа диаграммы следует, что векторы напряжения и тока совпадают по направлению. Сопротивление участка цепи постоянному току называется омическим, а сопротивление того же участка переменному току - активным сопротивлением.
|
||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.195.30 (0.009 с.) |

 I=
I= 
 Пусть существует система из n магнитносвязанных электрических цепей, в которых протекают постоянные токи. Пусть одна из цепей перемещается в направлении оси х на величину dx. При перемещении цепи будет выполнена механическая работа:
Пусть существует система из n магнитносвязанных электрических цепей, в которых протекают постоянные токи. Пусть одна из цепей перемещается в направлении оси х на величину dx. При перемещении цепи будет выполнена механическая работа: Изменение потокосцепления каждой цепи Ψk вызовет появление напряжения на ее зажимах:
Изменение потокосцепления каждой цепи Ψk вызовет появление напряжения на ее зажимах:  , при этом в системе будет выполнена дополнительная электрическая работа:
, при этом в системе будет выполнена дополнительная электрическая работа: , откуда следует, что
, откуда следует, что  ,, т. е. составляющая силы, действующей на электрическую цепь в произвольном направлении равна производной от энергии магнитного поля в этом же направлении.
,, т. е. составляющая силы, действующей на электрическую цепь в произвольном направлении равна производной от энергии магнитного поля в этом же направлении. ;
; Рассмотрим подключение R - L цепи к источнику постоянной ЭДС E (рис. 1 а)).
Рассмотрим подключение R - L цепи к источнику постоянной ЭДС E (рис. 1 а)).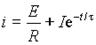 .
.

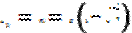


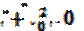 (1)
(1) - собственная циклическая частота контура,
- собственная циклическая частота контура,  - вторая производная заряда по времени.
- вторая производная заряда по времени.
 -максимальное значение заряда на обкладках конденсатора,
-максимальное значение заряда на обкладках конденсатора, 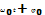 - фаза колебаний,
- фаза колебаний, 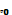 -начальная фаза. Значение собственной частоты колебаний
-начальная фаза. Значение собственной частоты колебаний  и
и  (3), где
(3), где 
 , или
, или  ) (4)
) (4) . Значение собственной циклической частоты колебаний в контуре определяется выражением:
. Значение собственной циклической частоты колебаний в контуре определяется выражением:  (5)
(5) период свободных колебаний в идеальном колебательном контуре будет определятся формулой Томсона:
период свободных колебаний в идеальном колебательном контуре будет определятся формулой Томсона:  (6)
(6) (1), где-коэффициент затухания. При
(1), где-коэффициент затухания. При  решением уравнения является функция:
решением уравнения является функция:

 принято называть периодом затухающих колебаний. При незначительном затухании(
принято называть периодом затухающих колебаний. При незначительном затухании( ) период затухающих колебаний практически равен периоду свободных незатухающих колебаний.
) период затухающих колебаний практически равен периоду свободных незатухающих колебаний.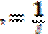 (3)
(3) (4),
(4), – количество колебаний за время релаксации, то логарифмическийдекремен затухания можно выразить иначе:
– количество колебаний за время релаксации, то логарифмическийдекремен затухания можно выразить иначе: (5)
(5) (6)
(6) (7)
(7) -амплитудное значение напряжения, -циклическая частота напряжения.
-амплитудное значение напряжения, -циклическая частота напряжения. подключить к сопротивлению R, то через него протекает ток
подключить к сопротивлению R, то через него протекает ток (1)
(1) (2)
(2) и
и  - комплексные амплитуды тока и напряжения.
- комплексные амплитуды тока и напряжения. 


