
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Линейное распределение электрических зарядовСодержание книги
Поиск на нашем сайте Расчет электростатического поля бесконечно длинной тонкой равномерно заряженной нити:
Алгоритм расчета электростатических полей: Ø из соображений симметрии системы определяем форму силовых линий поля; Ø выбираем удобную для нахождения потока форму замкнутой поверхности; Ø находим поток вектора напряженности электростатического поля через эту поверхность; Ø находим суммарный электрический заряд, который находится внутри этой поверхности; Ø подставляем полученные значения в теорему Гаусса и находим напряженность поля
Циркуляция и ротор векторного поля. Работа сил электростатического поля: потенциальный характер электростатического поля; разность потенциалов между двумя точками поля, потенциал в заданной точке поля; эквипотенциальные поверхности; расчет потенциала поля, создаваемого неподвижным точечным зарядом; принцип суперпозиции для потенциала. Потенциал электростатического поля в вакуме Работа силы:
Ротор векторного поля: (локальная характеристика). Разбираем поверхность, ограниченную
- циркуляция по контуру
Rot векторной величины является вектор. Rot – вихрь. Циркуляция приходящая на поверхность rot=0 когда проекция =0. Если работа силы = 0, то и rot=0 и циркуляция. Теорема Стокса:
циркул=0, то поле без вихревое. Потенцианальный характер электрического поля. Поскольку работа силы поля по перемещению в нем подобного электрический заряд не зависит от (перемещения) траектория движения, то электрического поля является потенциальной(безвихревым). Работа силы = 0.
только для поля неподвижного точечного заряда. Разность потенциалов между 2-мя точками поля. Разностью потенциалов или напряжением между 2-мя точками электростатического поля наз.отношение работы сил поля по перемещению пробного электрического заряда между данными точками к величине пробного заряда:
Потенциал в данной точке поля: Если электростатическое поле создало точечным электрическим зарядом q тогда
Потенциалом электростатического поля в точке называется отношение работы сил поля по перемещению пробного электрического заряда из данной точки в
Эквипотенциальной поверхностью наз. совокупность точек поля с равным потенциалом. Они применяют для графика изображения полей. Вычисление потенциала: Если электростатическое поле создано точечным электрическим зарядом q, тогда:
В соответствии с принципом суперпозиции электростатического поля потенциалы должны алгебраически суммированы:
Градиент скалярной функции. Связь между напряженностью электростатического поля и его потенциалом: математическая запись и физический смысл для однородного и неоднородного полей; применение для расчета полей. Уравнение Пуассона. ГРАДИЕНТ ФУНКЦИИ и = f(x, у, z), заданной в некоторой обл. пространства (X Y Z), есть вектор с проекциями Уравнение Пуассона — эллиптическое дифференциальное уравнение в частных производных, которое, среди прочего, описывает *электростатиче ское поле, *стационарное поле температуры, *поле давления, *поле потенциала скорости в гидродинамике. Это уравнение имеет вид: В трёхмерной декартовой системе координат уравнение принимает форму:
Нахождение φ для данного f — важная практическая задача, поскольку это обычный путь для нахождения электростатического потенциала для данного распределения заряда. В единицах системы СИ:
где
|
||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |




 -криволинейный интеграл.
-криволинейный интеграл. - циркуль вектора (интегральная хар.)
- циркуль вектора (интегральная хар.)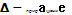 ;
;  ; в-диф=бесконечно малому приращению.
; в-диф=бесконечно малому приращению. , на элементарные площадки
, на элементарные площадки  ;
;
 ;
; - ротор вектора.
- ротор вектора. циркуляция вектора по замкнутому контуру =потоку. Rot через поверхность ограниченную этим контуром.
циркуляция вектора по замкнутому контуру =потоку. Rot через поверхность ограниченную этим контуром.




 к величине этого пробного заряда:
к величине этого пробного заряда: – потенциал поля в точке определен только для поля тех зарядов, которые ограничены в пространстве; если не ограничены, то
– потенциал поля в точке определен только для поля тех зарядов, которые ограничены в пространстве; если не ограничены, то 


 обозначаемый символами: grad
обозначаемый символами: grad  где i, j, k — координатные орты. Г. ф. — есть функция точки (х, у, z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигает наибольшего значения и равна:
где i, j, k — координатные орты. Г. ф. — есть функция точки (х, у, z), т. е. он образует векторное поле. Производная в направлении Г. ф. в данной точке достигает наибольшего значения и равна: 


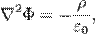
 — электростатический потенциал (в вольтах),
— электростатический потенциал (в вольтах),  — объёмная плотность заряда (в кулонах на кубический метр), а
— объёмная плотность заряда (в кулонах на кубический метр), а  —диэлектрическая проницаемость вакуума (в фарадах на метр).
—диэлектрическая проницаемость вакуума (в фарадах на метр).


