
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Логические элементы на КМОП-транзисторах.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Сокращение КМОП означает «комплементарные МОП-транзисторы». Также иногда используется сокращение COSMOS, которое обозначает «комплементарная симметричная МОП-структура». Симметричность КМОП-схем особенно хорошо видна в схеме элемента НЕ, рисунок 1.8. Если на входе А действует H уровень, то транзистор Т2 открыт, транзистор Т1 закрыт, и на выходе элемента Z имеется уровень L. Если на входе А действует L уровень, то транзистор Т2 закрыт, транзистор Т1 открыт, и на выходе элемента Z имеется уровень H.В КМОП-элементе один из транзисторов всегда закрыт, и такой элемент практически не потребляет ток. Только во время переключения от источника питания потребляется небольшой ток, так как оба транзистора одновременно, но ненадолго открыты. Один из транзисторов переходит из открытого состояния в закрытое, а другой, наоборот, из закрытого состояния переходит в открытое состояние.
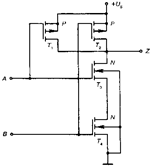
На рисунке 1.9 приведена схема КМОП И-НЕ элемента. Если на обоих входах действуют H уровни, то транзисторы Т1и Т2 закрыты, транзисторы Т3 и Т4 открыты, и на выходе элемента Z имеется уровень L. Если на один вход подан H уровень, а на другой – L уровень, то один из верхних транзисторов Т1 или Т2 открывается, а один из нижних транзисторов Т3 или Т4 закрывается. Через открытые транзисторы к выходу будет прикладываться H уровень. В семейство КМОП-схем входит несколько серий ИС. КМОП-серияCD4011Bявляется промышленным стандартом. Быстродействующая КМОП-серия 74HC00 по разъемам и функционально совместима с аналогичной ТТЛ-серией.
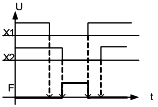
Реализация логических элементов НЕ, И, ИЛИ, ИЛИ-НЕ, И-НЕ на элементах 2ИЛИ-НЕ, 2И-НЕ. Синтез логических устройств по заданному логическому выражению. Реализация цифровой схемы в базисе ИЛИ-НЕ, И-НЕ. В цифровой эл-ке имеется набор ЛЭ, реализующих ф-и, с помощью которых могут быть получены все остальные ф-и булевой алгебры (конъюнкция, дизъюнкция, инверсия). К таким элементам относятся элементы И-НЕ и ИЛИ-НЕ. Логический элемент И-НЕ является комбинацией логич-х схем И и НЕ. На вых. логич-го эл-та И-НЕ сигнал уровня 0 будет только в том случае, когда на обоих его входах присутствует сигнал уровня 1. УГО, таблица истинности и диаграмма работы ЛЭ И-НЕ представлены в таблице 1.2. Логический элемент ИЛИ-НЕ явл-я комбинацией логич-х схем ИЛИ и НЕ. На выходе логич-го эл-та ИЛИ-НЕ сигнал уровня 1 будет только в том случае, когда на обоих его входах присутствует сигнал уровня 0. УГО, таблица истинности и диаграмма работы ЛЭ ИЛИ-НЕ представлены в таблице 1.2. Наименование.ЛогическоевыражениеЭлементИ-НЕ
ЭлементИЛИ-НЕ
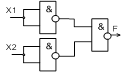
Преобразования выполняются с помощью теоремы Де-Моргана, правила двойного отрицания и правила повторения. Первая теорема Де-Моргана: Правило двойного отрицания: Преобразование функции ИЛИ (дизъюнкция) к базовому элементу И-НЕ осуществляется с помощью теоремы Де-Моргана, рисунок 1.4.а. Преобразование функции ИЛИ к базовому элементу ИЛИ-НЕ осуществляется согласно правилу двойного отрицания, рисунок 1.4.б.
Преобразование функции И (конъюнкция) к базовым элементам ИЛИ-НЕ и И-НЕ представлено на рисунке 1.5.
Преобразование функции НЕ (инверсия) к базовым элементам И-НЕ и ИЛИ-НЕ представлено на рисунке 1.6. Функция НЕ реализуется элементами И-НЕ или ИЛИ-НЕ при объединении их входов. Используется правило повторения.
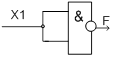
И-НЕ В качестве примера синтезируем на базовых ЛЭ цифровую схему, работа которой описывается логическим выражением (п.1.2): Цифровая схема на базовых ЛЭ И-НЕ, работа которой описывается логическим выражением
ИЛИ-НЕ В качестве примера синтезируем на базовых ЛЭ цифровую схему, работа которой описывается логическим выражением (п.1.2): Цифровая схема на базовых ЛЭ ИЛИ-НЕ, работа которой описывается логическим выражением
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 536; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |







 .Вторая теорема Де-Моргана:
.Вторая теорема Де-Моргана:  .
. .Правило повторения:
.Правило повторения: 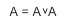 или
или 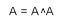 .
.







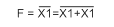

 .
. , представлена на рисунке 1.7.
, представлена на рисунке 1.7.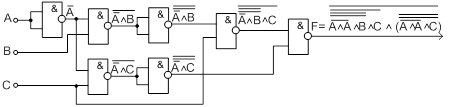
 .
.



