
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Синтез логических устройств по заданному логическому выражению.Содержание книги
Похожие статьи вашей тематики
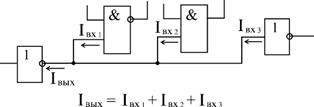
Поиск на нашем сайте На практике часто требуется синтезировать схему по заданному логическому выражению. В качестве примера синтезируем цифровую схему, работа которой описывается логическим выражением Определим количество входных сигналов. Из логического выражения видно, что входными сигналами являются сигналы А, В и С, т.е. схема будет иметь три входа. Реализовать логическое выражение схемотехнически возможно только пошагово: 1 шаг – получение инверсии входных сигналов В и С; 2 шаг – получение логических сумм сигналов 3 шаг – получение инверсии логической суммы сигнала 4 шаг – получение логической суммы сигналов Для получения Выражение К этому элементу последовательно подключается ЛЭ НЕ, обеспечивающий получение сигнала Выходы с сигналами
Для схемотехнической реализации логической суммы сигналов Цифровая схема, реализующая такое схемотехническое решение, представлена на рисунке 1.3.
15. Особенности проектирования цифровых схем. Общие требования к оформлению цифровых схем. При разработке цифрового прибора используются модели представления цифровых схем: логическая модель, модель с временными задержками, модель с учетом электрических эффектов (или электрическая модель).Первая модель применима для всех цифровых схем, работающих с низкой скоростью, в которых быстродействие не принципиально. Вторая модель учитывает задержки срабатывания логических элементов. Ее применение необходимо для всех быстродействующих устройств и для случая одновременного изменения нескольких входных сигналов. Третья модель учитывает входные и выходные токи, входные и выходные сопротивления и емкости элементов. Эту модель надо применять при объединении нескольких входов и выходов, при передаче сигналов на большие расстояния и при нетрадиционном включении логических элементов (с переводом их в аналоговый или в линейный режимы).На рисунке 1.14 на примере простейшего логического элемента инвертора показаны три модели представления этого цифрового «прибора».
Рис. 1.14 – Три модели представления цифрового устройства Из рисунка видно, что в первой, логической модели (1), считается, что элемент срабатывает мгновенно, любое изменение уровня входного сигнала сразу же, без всякой задержки приводит к изменению уровня выходного сигнала. Во второй модели (2) выходной сигнал изменяется с некоторой задержкой относительно входного. В третьей модели (3) выходной сигнал не только задерживается по сравнению с входным, но и его изменение происходит не мгновенно – процесс смены уровней сигнала (фронт сигнала) имеет конечную длительность. Кроме того, третья модель учитывает изменение уровней логических сигналов.В начале проектирования используется первая модель, а затем для некоторых узлов применяется вторая или (реже) и третья модель. При этом первая модель не требует вообще никаких цифровых расчетов, для нее достаточно только знание таблиц истинности или алгоритмов функционирования микросхем. Вторая модель предполагает расчет временных задержек элементов на пути прохождения сигналов, рисунок 1.15. В результате этого расчета может выясниться, что требуется внесение изменений в схему.
Рис. 1.15 – Суммирование задержек элементов Расчеты по третьей модели могут быть различными, в том числе и довольно сложными, но в большинстве случаев они все-таки сводятся всего лишь к суммированию входных и выходных токов логических элементов, рисунок 1.16.
Рис. 1.16 – Суммирование входных токов элементов В результате этих расчетов может выясниться, что требуется применение микросхем с более мощными выходами или включение дополнительных элементов. Общие требования к оформлению схем Все электрические схемы, выполняемые в рамках лабораторной работы, должны изображаться согласно требованиям ЕСКД: ГОСТ 2.702-75, 2.743-82, 2.708-81, 2.701-84 и т.д. Схемы электрические принципиальные являются основным чертежом лабораторных работ.Принципиальная схема определяет полный состав элементов и связей между ними. Все интегральные микросхемы и электронные компоненты на ней изображаются в виде их условно-графического обозначения (УГО), рисунок 1.17.
Рис. 1.17 – Условно-графическое обозначение и размеры ЛЭ с двумя входами При этом обязательно указывается нумерация выводов интегральной микросхемы. Выводы «Питание» и «Общий» могут не изображаться. Корпуса интегральных микросхем на чертежах должны иметь позиционное обозначение. Рекомендуется использовать следующее позиционное обозначение: DDN (N – номер очередного корпуса). Позиционное обозначение выполняется сверху вниз, слева направо. Для наглядного изображения схемы на чертеже корпус интегральной микросхемы может изображаться в конкретном месте по отдельным элементам. В этом случае при позиционном обозначении указывается также номер элемента в корпусе, например, DD2.1 (2-й корпус, 1-й элемент), рисунок 1.18.
Рис. 1.18 – Фрагмент схемы При возможности линии связи объединяются в шины, рисунок 1.19. Линия связи, которая входит в шину, должна иметь уникальный в пределах шины числовой номер или уникальное буквенно-цифровое обозначение. Отводы линий от шины рекомендуется выполнять под прямым углом. Шину на чертеже рекомендуется выполнять толщиной 2-3 мм. Толщина линий связи – не более 1 мм. Обозначение сигнала, входящего (выходящего) в (из) шины рекомендуется производить у самой шины. Обозначение сигналов, входящих в шину, должно однозначно соответствовать сигналам, выходящим из шины. Расстояние между линиями сигналов – не менее 0,5 см.На рисунке 1.20 показаны рекомендуемые размеры при изображении ЛЭ, линий связи и шин на принципиальной схеме. Все ответвления от линий связи на чертеже изображаются точками.
16. Преобразование и упрощение логических выражений. Упрощение логических функций с помощью карт Карно. Частично-определенная функция и ее упрощение. Сложность логической функции, а отсюда сложность и стоимость реализующей ее схемы пропорциональны числу операций и числу вхождений перемещений или их отрицаний. Логическая функция может быть упрощена с помощью аксиом и теорем алгебры логики, однако такие преобразования требуют громоздких выкладок и навыков. Для упрощения применяются правила, приведенные в таблице 1.1.Таблица 1.1 – Правила вычисления
Рассмотрим булево выражение: Карта Карно для 2-х переменных имеет вид, представленный на рисунке 1.1.а.
Минимизируем исходное логическое выражение посредством применения карты Карно. Поставим 1 в карте Карно в тех клетках, которые соответствуют наборам функции, присутствующим в логическом выражении, рисунок 1.1.б.Отыскание минимальной формы сводится к максимальному склеиванию по некоторому аргументу: по В – вертикаль и по А – горизонталь. Единицы, находящиеся в соседних клетках, объединим контурами (рисунок 1.1.в). Возможно объединение 2, 4, 8 и т.д. единиц, стоящих в соседних клетках. Кроме этого, карта Карно может быть свернута в горизонтальный или вертикальный цилиндры, или шар, что также позволяет объединить единицы, стоящие в соседних крайних клетках свернутых карт.Т.к. у нас два контура, то новое выражение будет состоять из двух членов, связанных функцией ИЛИ. Например, для нижнего контура аргумент А встречается с Рассмотрим пример построения карты Карно для трех переменных. Пусть дано логическое выражение:
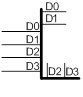
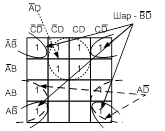
Рассмотрим пример построения карты Карно для четырех переменных, рисунок 1.3.
В рассмотренных примерах осуществлялась минимизация по 1, однако в некоторых случаях более удобной может оказаться минимизация по 0. Пример такого случая представлен на рисунке 1.4. Минимизация по нулям показана штрихпунктирной линией, а по единицам – сплошной.
При минимизации по нулям получается отрицательная функция. Поставив с двух сторон отрицание и используя теорему Де-Моргана, можно перейти к положительной функции и реализовать полученное значение на требуемых логических элементах:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-19; просмотров: 587; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.96 (0.009 с.) |


 и
и  ;
;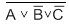 и
и  и
и  необходимы два элемента НЕ.
необходимы два элемента НЕ.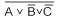 . Выражение
. Выражение 








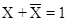


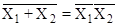


 . Для реализации данного выражения необходимо 2 инвертора, 3 конъюнктора (И) и 1 дизъюнктор (ИЛИ). Упростим данное логическое выражение:
. Для реализации данного выражения необходимо 2 инвертора, 3 конъюнктора (И) и 1 дизъюнктор (ИЛИ). Упростим данное логическое выражение: 
 .Таким образом, все логическое выражение сведено к логической операции ИЛИ.На практике для упрощения логических выражений, описывающих работу устройства, применяют карты Карно. Карта Карно представляет собой графическое изображение всех возможных наборов значений аргументов, каждый минтерм изображается на карте в виде клетки. Карта образуется путем такого расположения клеток, при котором минтермы, находящиеся в соседних клетках, отличаются значением одной переменной.
.Таким образом, все логическое выражение сведено к логической операции ИЛИ.На практике для упрощения логических выражений, описывающих работу устройства, применяют карты Карно. Карта Карно представляет собой графическое изображение всех возможных наборов значений аргументов, каждый минтерм изображается на карте в виде клетки. Карта образуется путем такого расположения клеток, при котором минтермы, находящиеся в соседних клетках, отличаются значением одной переменной.


 и В, но в соответствии с правилом булевой алгебры аргументы
и В, но в соответствии с правилом булевой алгебры аргументы  .Карта Карно и результат минимизации представлены на рисунке 1.2.
.Карта Карно и результат минимизации представлены на рисунке 1.2.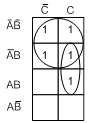
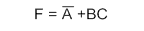




 ,
,  ,
, 



