Максимальная динамическая нагрузка

 

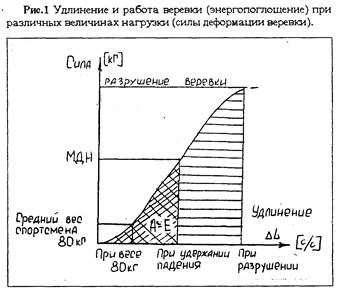
В конце свободного падения энергия тела равна произведе­нию веса падающего тела (G) на глубину падения (Н). Что­бы остановить падение, веревке необходимо произвести опреде­ленную работу деформации (А), которая равна энергии па­дения (Е).

Это можно проиллюстрировать на графике, пока­зывающем зависимость удлинения веревки от величины прило­женной к ней силы (Рис. 1).

 

 

Так как работа равна величие силы помноженной на изме­нение пути (в нашем случае путь равен удлинению веревки), то площадь между кривой и осью абсцисс равна работе, совер­шенной веревкой при задержании падения.

Деформация растягивающейся под действием падающего тела веревки порождает силу торможения падения, величина которой до тех пор непрерывно нарастает, пока работа тормо­жения (А), совершаемая веревкой, не поглотит (станет равна) энергию его падения (Е).

В момент остановки падения сила торможения (вызванная деформацией веревки) достигает своей максимальной величи­ны.

Максимальная величина силы торможения (которой она достигает при остановке падения) называется МАКСИМАЛЬ­НОЙ ДИНАМИЧЕСКОЙ НАГРУЗКОЙ (МДН).

Другими словами, МДН - это максимальная величина силы динамического удара, который страховочное снаряжение и человеческое тело выдерживают в момент, когда падение уже остановлено веревкой и она перестала удлиняться.

Это понятно. А вот сейчас - внимание!

Величина МДН НЕ ЗАВИСИТ от абсолютной высоты падения, а определяется ТОЛЬКО фактором падения и динамическими качествами веревки.

Понимание этого положения встречает определенные труд­ности, так как наше сознание не может смириться с мыслью, что падение, к примеру, со 100 метров приводит к такому же динамическому удару, как и падение с каких-нибудь 10 метров.

Не очевидно. Тем не менее, это так, если в обоих случаях паде­ние остановлено веревкой с одинаковыми динамическими каче­ствами и само падение носит одинаковый характер (имеет оди­наковый фактор падения).

Рассмотрим эти понятия повнимательнее.

 

 

ДИНАМИЧЕСКИЕ КАЧЕСТВА ВЕРЕВКИ

Под динамическими качествами веревки следует понимать, прежде всего, ее способность к удлинению. При одинаковой энергии падения МДН всегда будет ниже для веревки более эластичной и выше для веревки с меньшей способностью к уд­линению (Рис.2).

Экспериментально установлено, что величина максималь­ной динамической нагрузки зависит не от энергии падения как таковой, а, главным образом, от способности веревки удли­няться в большей или меньшей степени при данном факторе падения.

 

Рис.2 Зависимость МДН от динамических качеств веревки.

 

Таким образом, представление о том, что определенной высо­те падения соответствует строго определенная величина МДН столь же неверно, как и попытка рассуждать о безопасности хождения по одинарной веревке, руководствуясь только дан­ными о ее прочности.

 

Разные веревки имеют различные динамические качества, то есть способность удлиняться под нагрузкой. Поэтому при оди­наковой высоте и факторе падения в разных веревках возни­кают разные величины максимальных динамических нагрузок. Более прочная, но менее эластичная веревка при удержании падения испытывает более высокую динамическую нагрузку и наоборот.

Именно это положение определяет возникновение недопустимо больших динамических нагрузок при использова­нии стального троса в качестве линейной опоры для страхо­вочных операций. Стальной трос имеет ничтожную способность к удлинению при нагрузке, а значит, даже малейшее падение на тросе приведет к возникновению сильного динамического удара на все элементы страховочной цепи.

 

ПОЛЕЗНО ЗНАТЬ:

- Конкретная величина МДН изменяется в широких преде­лах. Она не зависит от абсолютной высоты падения, как от отдельно взятой величины, а определяется исключительно ди­намическими качествами веревки и фактором падения.

- Под динамическими качествами веревки следует понимать, прежде всего, ее способность к удлинению.

 

ФАКТОР ПАДЕНИЯ

Вопрос о факторе падения довольно подробно рассмотрен в альпинистской литературе, но кажется полезным напомнить читателю основные положения.

В советской практике фактор падения иногда называется "коэффициентом падения".

Что же такое фактор или коэффициент падения?

Фактором падения называется отношение между высотой (глубиной) падения (Н) и длиной веревки (L), которая это падение останавливает:

f = H/L.

От этого отношения зависит так называемая "степень" или "тяжесть" падения, и, прежде всего, нагрузка на страховочную цепь при удержании веревкой падающего тела.

Разберемся, почему это так.

Предположим, что мы подняли тело весом P на 2 метра над точкой закрепления веревки А (Рис. 3 а).

 

 

Если тело отпустить, то до того момента как веревка начнет растягиваться, глубина его падения (Н), будет равна 4 метрам, то есть двум длинам L веревки.

В этом случае фактор падения равен:

f = H/L = 4/2 = 2.

Эта цифра означает, что при удержании падающего тела на каждый метр веревки приходится энергия, равная энергии сво­бодного падения данного тела с высоты 2 м.

То есть (предположив вес падающего равным 80 кг):

80 кг веса падающего, помноженные на 4 м глубины падения дадут:

80 кг х 4 м = 320 кгм энергии падения.

320 кгм энергии падения, распределенной на 2 м дли­ны имеющейся в распоряжении веревки:

320 кгм: 2 м = 160 кгм/м.

Это означает, что каждый метр веревки за счет своей деформации должен поглотить (амортизировать) 160 кгм энергии падения.

Иными словами фактор падения определяет так называемую ОТНОСИТЕЛЬНУЮ глубину падения, то есть, сколько метров свободного падения приходится на каждый метр веревки, уча­ствующей в удержании данного падения.

Энергия падения распределяется в одинаковой степени на каждый метр веревки, и каждый ее метр испытывают одинаковое элементарное относительное удлинение.

Общее удлинение веревки пропорционально общей ее длине.

Следовательно, способность каждой конкретной веревки поглощать энер­гию будет тем больше, чем больше будет ее длина.

Поэтому усилия в веревке при удержании динамического рывка зави­сят не от абсолютной глубины падения, а лишь от ее относительной величины, - то есть от фактора падения.

Подтвердим этот вывод, подняв тело Р не на 2, а на 20 м над точкой закрепления.

В этом случае понадобится веревка длиной 20 м, а глубина свободного падения возрастает до 40 м.

Фактор же падения в этом случае не изменится:

f = 40/20 = 2

Не изменится и энергия, приходящаяся на каждый метр ве­ревки.

С одной стороны:

80 кг х 40 м глубины падения = 3200 кгм энергии!

Однако 3200 кгм: 20 м длины веревки = 160 кгм/м.

Все те же 160 кгм, которые предстоит самортизировать каждому метру веревки!

Это значит, что величина нагрузки - рывка, приходящегося на веревку, останется со­вершенно такой же, как и при падении на глубину 4 м.

Казалось бы, невероятно, но факт. Фактор падения остался одним и тем же, и нагрузки при удержании рывка не изменились, хоть полет был в десятки раз больше.

Несмотря на то, что во втором случае энергия падения в 10 раз больше, но она и распределяется по веревке в 10 раз боль­шей длины, а значит имеющей в 10 раз бОльшую способность поглощать энергию.

Значит, при одном и том же факторе паде­ния работа торможения, производимая в процессе деформации каждым метром веревки, независимо от абсолютной глубины падения, будет одинакова.

 

Поэтому и величина МДН (максимальной динамической нагрузки) для данной верев­ки будет одинаковой как при падении на 2 метра, так и на 10 метров. Каким бы странным и не очевидным это ни казалось.

То есть при равных остальных услови­ях (масса тела, динамические качества веревки и пр.), величина максимальной динамической нагрузки, возникающей в момент остановки и зависания на веревке па­дающего тела не зависит от абсолютной глубины падения, а зависит только от его фактора.

Чем меньше окажется фактор падения, тем меньше будет величина ди­намического рывка и наоборот.

Во втором примере (Рис. 3 б) глубина свободного падения равна длине веревки, то есть срыв произошел от точки закрепления веревки.

При таком раскладе фактор падения будет равен:

f =2/2 = 1.

В этом случае нагрузка на страховочную цепь и главную ее составляющую - веревку, будет значительно меньше, так как каждый ее метр будет амортизировать энергию падения того же тела, но с высоты всего 1 метр:

80 кг веса х 2 м глубины падения = 160 кгм энергии;

160 кгм: 2 метра веревки = 80 кгм/м на каждый метр веревки.

Вдвое более легкие условия.

Максимальный фактор падения - 2.

Это наиболее тяжелая степень падения на глубину, равную двойной длине веревки. Вероятность такого падения никогда не исключена при свобод­ном лазании, если первый в связке срывается в момент, когда веревка между партнерами еще не закреплена на промежуточ­ных крючьях.

Однако если не говорить о восхождениях с нижней стра­ховкой, при правильно оборудованных отвесах возможные падения всегда будут много более низкой степени: в большин­стве случаев фактор падения не превышает значений 0,3 - 0,5.

Именно это позволяет в практике вертикальной спелеологии и при спасательных операциях применять мало эластичные, так называемые, статические веревки и стальной трос.

В принципе, при восхождениях с нижней страховкой возможны падения лидера связки с фактором даже превышающим максимальное значение 2.

Если после срыва лидера страхующий умудрится несколько выбрать страховочную ве­ревку, а потом жестко закрепить ее без протравливания, то на каждый ее метр придется энергия выше, чем обычные 2 к 1.

Но в реальных условиях это очень маловероятно.

 

Еще более тяжелые факторы падения возникают при срывах со скользящей страховкой за установленные перила, подобные "Виа Феррата" (Via Ferrata), характерные для альпийских горных маршрутов.

Вообще, понятие фактора падения нуждается в более детальном рассмотрении, если мы начинаем говорить о сложных системах самостраховки, но это отдельная тема, а пока продолжим.

Каким образом мы можем влиять на величину фактора па­дения?

Прежде всего, грамотно навешивая веревку. Следует внима­тельно следить за тем, чтобы длина используемой веревки всегда была сопоставимой с глубиной возможного падения в случае каких-либо неприятностей на отвесе.

Во-вторых, не попадая в положения, когда возможны тяжелые падения. То есть не выходя над точкой закрепления веревки без серьезной к тому необходимости.

Именно величина факто­ра возможного падения всецело находится в наших руках. Поэтому и о значениях максимальной дина­мической нагрузки, возникающей в страховочной цепи, следует говорить только для данной, заданной нашими сознатель­ными действиями, величины фактора падения.

К примеру, зна­чения МДН для динамической альпинистской веревки приво­дятся в ее паспортах для фактора падения 1,78, что соответст­вует среднестатистической ситуации срыва и падения лидера связки при восхождении с нижней динамический страховкой.

Значения же МДН для статических спелеоверевок определяются для фактора падения 1,0, то есть наиболее вероятного макси­мального фактора падения при разрушении точек закрепления навески и т.п.

Следует иметь ввиду, что приводимые в паспортах веревок значения МДН определяются для ПЕРВОГО испытательного рывка.

Важно понимать, что если веревку, выдержавшую ди­намический удар, использовать для удержания еще одного па­дения, аналогичного первому, то при этом величина максимальной динамической нагрузки неизбежно возрастет, так как при первом рывке часть волокон будет необратимо де­формировано, и ее динамические качества веревки несколько ухудшат­ся.

Именно поэтому опытные восходители по возвращении с горы немедленно заменяют веревку, если ею был остановлен хотя бы один серьезный срыв.

И правильно делают.

 

 

2.7. ГРАНИЦА Но ("Аш-нулевое")

Как видно из Рис.4 сила нагрузки на веревку до тех пор не может достичь максимума для данного фактора падения, поку­да длина веревки (L), а соответственно и высота падения (Н), будут меньше некоторой минимальной величины.

Это так на­зываемая граница Но, после которой величина МДН входит в соответствие с величиной фактора падения.

Почему это проис­ходит?

 

Осуществим ряд последовательных падений одного и того же груза с фактором 1, но в каждом последующем случае будем останавливать его падение все более длинным куском веревки. Если измерить величины возникающих при этом динамических нагрузок, то мы получим кривую, которая вначале стремительно идет вверх, а затем все более выполаживается, пока не достигает некоей границы Но (Рис.5).

После этого график превращается в линию параллельную оси абсцисс: МДН стала постоянной, то есть такой, какой она и должна быть в случае, когда фактор падения тоже постоянен.

 

 

Полезный эффект снижения величины МДН, действующей на веревку при ее длине, меньшей границы Но, отчасти объясняет­ся тем, что часть энергии падения поглощается трением между витками узлов и деформацией составляющей узлы веревки. При небольших глубинах падения эта часть сопоставима с общей энергией падения. Таким образом, доля узлов в общем энерго­поглощении достаточно значительна и поэтому заметна. При больших глубинах падения узлы точно также амортизируют часть энергии падения, но доля их на, общем фоне становится пренебрежимо мала.

Однако отметим этот факт: узлы на веревке амортизируют часть энергии падения.

Эффект границы Но имеет практическое значение для корот­ких кусков веревки, снижая возможные динамические нагруз­ки. Например, в случае с самостраховочными "усами", или для участков веревки, связывающих основные и дублирующие за­крепления. Поэтому не стоит стремиться затягивать узлы уси­лием, превышающим вес человека.

Величина границы Но непосредственно зависит от вида ве­ревки, а также от ее состояния - мокрая или сухая, более или менее изношенная и т.п.

В целях практической работы можно принять, что для дина­мических веревок их длина, при которой сколько-нибудь за­метно проявляется эффект границы Но, будет порядка 1,5 м, а для статических веревок - не более 1 м с учетом завязанных на конце веревки узлов.