
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Параметры асинхронной машины для номинального режимаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Параметрами асинхронной машины называют активные и индуктивные сопротивления обмоток статора х1, r1, ротора r2, x2, сопротивление взаимной индуктивности х12 и расчетное сопротивление r12 (или rm), введением которого учитывают влияние потерь в стали статора на характеристики двигателя. Схемы замещения фазы асинхронной машины, приведены на рис. 1.35. Физические процессы в асинхронной машине более наглядно отражает схема, изображенная на рис. 1.35,а. Но для расчета удобнее схема, показанная на рис. 1.35, б.
Рис. 1.35 Схемы замещения фазы обмотки приведенной асинхронной машины.
С увеличением нагрузки увеличивается поток рассеяния и в связи с этим из-за возрастания насыщения отдельных участков магнитопровода полями рассеяния уменьшаются индуктивные сопротивления х1 и x2. Увеличение скольжения в двигателях с короткозамкнутым ротором приводит к возрастанию действия эффекта вытеснения тока, что вызывает изменение сопротивлений обмотки ротора r2 и x2. При расчете рабочих режимов машины в пределах изменения скольжения от холостого хода до номинального эти изменения незначительны и ими обычно пренебрегают. При расчете пусковых режимов, в которых токи машины в несколько раз превышают номинальный, а частота тока в роторе близка к частоте питающей сети, приходится учитывать изменение параметров от насыщения участков магнитопровода полями рассеяния и от влияния эффекта вытеснения тока.
а) Активные сопротивления обмоток статора
Активные сопротивления r1 и r2, Ом, определяются по основной расчетной формуле
где L — общая длина эффективных проводников фазы обмотки, м; qэф — сечение эффективного проводника, м2:
qэл - сечение элементарного проводника; nэл - число элементарных проводников в одном эффективном; а - число параллельных ветвей обмотки; rJ - удельное сопротивление материала обмотки при расчетной температуре, Ом×м; kr - коэффициент увеличения активного сопротивления фазы обмотки от действия эффекта вытеснения тока. Таблица 1.19 удельные сопротивления материалов обмоток,
В проводниках обмотки статора асинхронных машин эффект вытеснения тока проявляется незначительно из-за малых размеров элементарных проводников. Поэтому в расчетах нормальных машин, как правило, принимают kr =1. Некоторое увеличение потерь, обусловленное действием эффекта вытеснения тока, относят к дополнительным потерям. Общая длина проводников фазы обмотки L, м,
где lср — средняя длина витка обмотки, м; W — число витков фазы. Среднюю длину витка lср находят как сумму прямолинейных пазовых и изогнутых лобовых частей катушки
Длина пазовой части lп равна конструктивной длине сердечников машины:
Катушки всыпной обмотки статора. Длина лобовой части, м,
вылет лобовых частей обмотки, м,
В этих формулах bкт — средняя ширина катушки, м:
b1 — относительное укорочение шага обмотки статора. Для диаметральных двухслойных обмоток, выполненных без укорочения шага, и для однослойных обмоток, включая обмотки из концентрических катушек, имеющих разную ширину, принимают b =1; Кл и Kвыл — коэффициенты, значения которых берут из табл. 1-19; В — длины вылета прямолинейной части катушек из паза от торца сердечника до начала отгиба лобовой части, м.
Для всыпной обмотки, укладываемой в пазы до запрессовки сердечника в корпус, берут В =0,01 м. В машинах, обмотки которых укладывают после запрессовки сердечника в корпус, вылет прямолинейной части В =0,015 м. Таблица 1.20 К расчету размеров лобовых частей катушек всыпной обмотки
б) Индуктивные сопротивления обмотки статора двигателей с фазными роторами
Индуктивные сопротивления обмоток двигателей с фазными роторами рассчитывают по:
Входящие в эту формулу коэффициенты магнитной проводимости обмоток асинхронных машин определяют следующим образом. Коэффициент магнитной проводимости пазового рассеяния lп рассчитывают по формулам, приведенным в табл. 1.22,в зависимости от конфигурации паза и расположения в нем проводников обмотки. В этих формулах значения коэффициентов kb и При диаметральном шаге двухслойных обмоток и для всех однослойных обмоток kb = При двухслойной обмотке с укорочением 2/3 £ b <1
при укорочении 1/3 £ b £ 2/3
коэффициент kb = 0,25 (1 + 3
Рис. 1.38 К расчету коэффициентов магнитной проводимости пазов статора.
Коэффициент магнитной проводимости лобового рассеяния
где q, 1л и b — число пазов на полюс и фазу, длина лобовой части катушки и относительное укорочение шага обмотки, для которой производится расчет. Для одно-двухслойных обмоток b находится соответственно:
При наличии радиальных вентиляционных каналов для обмотки статора
и для обмотки ротора
Таблица 1.22 Расчетные формулы для определения коэффициента магнитной проводимости пазового рассеяния фазных обмоток lП
Коэффициент магнитной проводимости дифференциального рассеяния для обмоток статора и фазного ротора
Значение коэффицинта x зависит от числа q, укорочения шага обмотки и размерных соотношений зубцовых зон и воздушного зазора.
Рис. 1.39 Коэффициенты к расчету проводимости дифференциального рассеяния. а - коэффициент DZ в зависимости от размерных соотношений b Ш/ t и b Ш/d; б - коэффициент k ' в зависимости от дробной части числа q; в - коэффициент k '' в зависимости от укорочения шага обмотки b; г - коэффициент
Ниже приводятся формулы, в которые при расчете x для обмоток статора или ротора следует подставлять данные обмоток и зубцовых зон соответственно статора или ротора. Для обмоток статора и ротора при q, выраженном целым числом (q ³2), для обмотки с диаметральным шагом
при укороченном шаге обмотки y = bt
при дробном q ³ 2
при дробном q, значение которого 1< q <2,
В этих формулах коэффициенты D z, k’, k’’ и
в) Сопротивления обмоток двигателей с короткозамкнутыми роторами
Активное сопротивление фазы обмотки статора двигателя с короткозамкнутым ротором рассчитывается так же, как и для двигателя с фазным ротором. Активное сопротивление фазы короткозамкнутого ротора r2 является расчетным, полученным из условия равенства электрических потерь в сопротивлении r2 от тока Iс и суммарных потерь в стержне и участках замыкающих колец реальной машины:
где Iс — ток в стержне ротора; Iкл — ток в замыкающих кольцах; rc — сопротивление стержня; rкл — сопротивление участка замыкающего кольца, заключенного между двумя соседними стержнями (см. рис. 1.24). Ток Iс называют током ротора и в расчетах обозначают I2. Учитывая, что Iкл = Ic /D = I2 /D, где
где
В этих выражениях lс — полная длина стержня, равная расстоянию между замыкающими кольцами, м; Dкл,ср — средний диаметр замыкающих колец, м (см. рис. 1.26): Dкл,ср = D2 – bкл; (1.167) qc — сечение стержня, м2; kr — коэффициент увеличения активного сопротивления стержня от действия эффекта вытеснения тока, при расчете рабочих режимов в пределах изменения скольжения от холостого хода до номинального, для всех роторов принимают kr =1; qкл — площадь поперечного сечения замыкающего кольца, м2; rс и rкл — соответственно удельные сопротивления материала стержня и замыкающих колец, Ом×м, при расчетной температуре 75°C. Сопротивление r2 должно быть приведено к числу витков первичной обмотки.
Индуктивное сопротивление рассеяния обмотки статора асинхронного двигателя с короткозамкнутым ротором
Коэффициенты магнитной проводимости пазового рассеяния lп определяются по формулам табл. 1.22. Коэффициент магнитной проводимости лобового рассеяния lл определяется по (1.154). Коэффициент магнитной проводимости дифференциального рассеяния lд1 определяют по формуле
в которой x находится следующим образом: При открытых пазах статора и отсутствии скоса пазов статора или ротора
При полузакрытых или полуоткрытых пазах статора с учетом скоса пазов
В этих формулах t1 и t2 — зубцовые деления статора и ротора; D z определяют по кривой рис. 1.39, а; kb определяют по (1.153); bск = bск / t2 — коэффициент скоса, выраженный в долях зубцового деления ротора. При отсутствии скоса пазов bск =0; Индуктивное сопротивление обмотки короткозамкнутого ротора определяют по формуле
полученной после подстановки в
значений m2 = Z2 и q2 =1/2 р обмотки короткозамкнутого ротора. Коэффициент магнитной проводимости пазового рассеяния обмотки короткозамкнутого ротора рассчитывают по приведенным в табл. 1.23 формулам в зависимости от конфигурации паза ротора на рис. 1.40. Коэффициент магнитной проводимости дифференциального рассеяния обмотки короткозамкнутого ротора
где
D z находят по кривым рис. 1.39, а.
Рис. 1.40 К расчету магнитной проводимости пазов ротора.
При большом числе пазов ротора, приходящихся на пару полюсов, Z2 / р ³10 можно принять x =1—D z. Коэффициент магнитной проводимости лобового рассеяния рассчитывают по следующим формулам. В роторах с литыми обмотками при замыкающих кольцах, прилегающих к торцам сердечника ротора (см. рис. 1.26, б), используют формулу
Если замыкающие кольца отставлены от торцов сердечника ротора (см. рис, 1.26, а), как, например, в обмотке, выполненной из медных или латунных стержней, впаянных в замыкающие кольца, расчет проводят по формуле
где Dкл.ср — средний диаметр замыкающих колец по (1.167); D=2sin pp / Z2 — коэффициент приведения токов в кольце к току в стержне; aкл и bкл — средние высота и ширина колец (см. рис. 1.26); Приведенное к числу витков первичной обмотки индуктивное сопротивление рассеяния фазы ротора
Сопротивление схемы замещения rm (см. рис. 1.35, а) должно быть взято таким, чтобы выделяющаяся в нем активная мощность была бы равна мощности, затрачиваемой на потери в стали в реальной машине и отнесенной к одной фазе. Таким образом, Таблица 1.23 Расчетные формулы для определения коэффициента магнитной проводимости пазового рассеяния короткозамкнутых роторов
Сопротивление взаимной индукции обмоток статора и ротора хm по схеме замещения может быть определено как хm = Е1 / Im. В расчетной практике параллельное включение сопротивлений rm и хm оказалось удобнее заменить последовательно включенными сопротивлениями r12 и x12 (см. рис. 1.35, б), значения которых с достаточной точностью определяют по следующим формулам:
г) Относительные значения параметров Параметры асинхронных машин обычно выражают в относительных единицах, принимая за базисные значения номинальное фазное напряжение и номинальный фазный ток статора. Значения параметров, выраженные в относительных единицах, будем отмечать звездочкой:
Относительные значения индуктивных сопротивлений рассеяния обмотки статора и приведенного сопротивления обмотки ротора различных асинхронных двигателей нормального исполнения находятся в пределах x1* =0,08…0,14 и Относительные значения сопротивлений взаимной индукции x12 *=2…4. Относительные значения активных сопротивлений обмотки статора и приведенного сопротивления обмотки ротора r1 *» Сопротивление r12 * обычно составляет 0,05…0,2.
д] Учет скоса пазов Скос пазов уменьшает влияние высших гармонических и улучшает виброакустические характеристики двигателей, но при скошенных пазах несколько уменьшается ЭДС обмоток. В практических расчетах уменьшение ЭДС от скоса пазов непосредственно не определяют, а влияние скоса учитывают увеличением индуктивных сопротивлений рассеяния обмоток статора и ротора. С этой целью в расчетную формулу (1.173) вводят коэффициент sск. Индуктивное сопротивление обмоток при скошенных пазах
Приближенное значение коэффициента sск можно найти по формуле
где bск — скос пазов в линейных размерах. Скошенные пазы выполняют большей частью лишь в двигателях с короткозамкнутыми роторами с h £160 мм. При скосе пазов из-за увеличения индуктивных сопротивлений рассеяния несколько уменьшается перегрузочная способность и пусковой момент двигателя. Поэтому в серии 4А роторы всех двигателей с высотой оси вращения h <160 мм выполняют со скосом пазов на одно зубцовое деление ротора, т.е. bск = t2.
ПОТЕРИ И КПД Потери в асинхронных машинах подразделяют на потери в стали (основные и добавочные), электрические потери, вентиляционные, механические и добавочные потери при нагрузке. Основные потери в стали в асинхронных двигателях рассчитывают только в сердечнике статора, так как частота перемагничивания ротора, равная f2 = sf1, в режимах, близких к номинальному, очень мала и потери в стали ротора даже при больших индукциях незначительны. В пусковых режимах электрические потери в обмотках во много раз превышают потери номинального режима, поэтому пренебрежение потерями в стали ротора при больших скольжениях не вносит сколько-нибудь заметной погрешности в расчет. Основные потери в стали статоров асинхронных машин определяют по следующей формуле
где b — показатель степени и р1,0/50 — удельные потери, Вт/кг, по данным [12] берут из табл. 1.24; kда и kдz — коэффициенты, учитывающие влияние на потери в стали неравномерности распределения потока по сечениям участков магнитопровода и технологических факторов. Для машин мощностью меньше 250 кВт приближенно можно принять kда =1,6 и kдz =1,8; для машин большей мощности kда =1,4 и kдz =1,7 Вa и Вzср — индукция в ярме и средняя индукция в зубцах статора, Тл; mа, mz1 — масса стали ярма и зубцов статора, кг:
hа — высота ярма статора, м: ha = 0,5 (Dа - D) – hп1; hz1 — расчетная высота зубца статора, м; bz1ср — средняя ширина зубца статора, м:
gс — удельная масса стали; в расчетах принимают gс =7,8×102 кг/м3. Добавочные потери в стали, возникающие при холостом ходе, подразделяют на поверхностные (потери в поверхностном слое коронок зубцов статора и ротора от пульсации индукции в воздушном зазоре) и пульсационные потери в стали зубцов (от пульсации индукции в зубцах). Вначале находят амплитуду пульсации индукции в воздушном зазоре над коронками зубцов статора и ротора, Тл, B 01(2) = b 01(2) kdBd. (1.186) Для зубцов статора b 01 зависит от отношения ширины шлица пазов ротора к воздушному зазору b 01= f (bш2 / d), для зубцов ротора — от отношения ширины шлица пазов статора к воздушному зазору b 02= f (bш1 / d). Зависимость b 0= f (bш / d) приведена на рис. 1.41. По В0 и частоте пульсаций индукции над зубцами, равной Z2n для статора и Z1n для ротора, рассчитывают удельные поверхностные потери, т. е. потери, приходящиеся на 1 м2 поверхности головок зубцов статора и ротора: для статора
для ротора
В этих выражениях k 01(2) — коэффициент, учитывающий влияние обработки поверхности головок зубцов статора (ротора) на удельные потери; если поверхность не обрабатывается (двигатели мощностью до 160 кВт, сердечники статоров которых шихтуют на цилиндрические оправки), то k 01=1,4¸1,8, при шлифованных поверхностях (наружная поверхность роторов машин средней и большой, мощности и внутренняя поверхность статора двигателей P2 >160 кВт) k 01(2)=1,7¸2,0; n = nc (1—s)» nс — частота вращения двигателя, об/мин. Полные поверхностные потери статора, Вт,
Полные поверхностные потери ротора, Вт,
Для определения пульсационных потерь вначале находится амплитуда пульсаций индукции в среднем сечении зубцов Впул, Тл: для зубцов статора
для зубцов ротора
В этих формулах Вz1ср и Вz2ср — средние индукции в зубцах статора и ротора, Тл;
При открытых пазах на статоре или на роторе при определении g 1 и g 2 в (1.193) вместо bш1 или bш2 подставляют расчетную ширину раскрытия паза, равную
индекс 1 — при расчете Значения коэффициента cd в зависимости от отношения bп / d для открытых пазов приведены на рис. 1.42. Пульсационные потери в зубцах статора
пульсационные потери в зубцах ротора
В этих формулах mz1 — масса зубцов стали, кг, определяется по (1.185); mz2 — масса стали зубцов ротора, кг:
где hz 2 — расчетная высота зубца ротора, м; bz 2 ср — средняя ширина зубца ротора, м: bz 2 ср = (bz 2 max + bz 2 min )/2.
Таблица 1.24 Удельные потери в стали асинхронных двигателей и значения b при толщине листов 0,5 мм
Таблица 1.25 К расчету механических потерь двигателей большой мощности
Поверхностные и пульсационные потери в статорах двигателей с короткозамкнутыми или фазными роторами со стержневой обмоткой обычно очень малы, так как в пазах таких роторов мало bш2 и пульсации индукции в воздушном зазоре над головками зубцов статора незначительны. Поэтому расчет этих потерь в статорах таких двигателей не производят. Таким образом, добавочные потери в стали
и общие потери в стали асинхронных двигателей
Обычно Рст,доб — приблизительно на порядок меньше по сравнению с Рст,осн. Электрические потери в асинхронных двигателях рассчитывают раздельно в обмотках статоров и роторов. Электрические потери во всех фазах обмотки статора, Вт,
Электрические потери в обмотке короткозамкнутого ротора, Вт,
или
Механические и вентиляционные потери. Потери на трение в подшипниках и вентиляционные потери в двигателях с радиальной системой вентиляции без радиальных вентиляционных каналов, с короткозамкнутым ротором и вентиляционными лопатками на замыкающих кольцах, Вт,
Кт =5 при 2 р =2, Кт =6 при 2 р ³4 для двигателей с Da £0,25 м; Kт =6 при 2р=2; Kт =7 при 2 p ³4 для двигателей с Da >0,25 м. В двигателях с внешним обдувом (0,1£ Da £0,5 м)
Kт =1 для двигателей с 2 р =2 и Кт =1,3 (1— Da) при 2 р ³4. В двигателях с радиальной системой вентиляции средней и большой мощности
где nк — число радиальных вентиляционных каналов; при отсутствии радиальных каналов nк =0. В двигателях с аксиальной системой вентиляции
где Dвент — наружный диаметр вентилятора, м; в большинстве конструкций можно принять Dвент» Da; Кт =2,9 для двигателей с Da £0,25 м; Кт =3,6 для двигателей с Da =0,25¸0,5 м. В двигателях большой мощности (0,5< Da <0,9 м)
В этом выражении коэффициент Кт берется из табл. 1.25. Добавочные потери при нагрузке асинхронных двигателей возникают за счет действия потоков рассеяния, пульсаций индукции в воздушном зазоре, ступенчатости кривых распределения МДС обмоток статора и ротора и ряда других причин. В короткозамкнутых роторах, кроме того, возникают потери от поперечных токов, т. е. токов между стержнями, замыкающихся через листы сердечника ротора. Эти токи особенно заметны при скошенных пазах ротора. В таких двигателях, как показывает опыт эксплуатации, добавочные потери при нагрузке могут достигать 1—2% (а в некоторых случаях даже больше) от подводимой мощности. ГОСТ устанавливает средние расчетные добавочные потери при номинальной нагрузке, равные 0,5% номинальной мощности. При расчетах потерь и КПД двигателей в режимах, отличных от номинального, значение добавочных потерь пересчитывают пропорционально квадрату токов:
Коэффициент полезного действия двигателя
где å P — сумма всех потерь в двигателе, Вт. Ток холостого хода двигателя
При определении активной составляющей тока холостого хода принимают, что потери на трение и вентиляцию и потери в стали при холостом ходе двигателя такие же, как и при номинальном режиме. При этом условии
Электрические потери в статоре при холостом ходе приближенно принимаются равными
Реактивная составляющая тока холостого хода Iх,х,р» Im. Коэффициент мощности при холостом ходе
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1409; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.013 с.) |


 (1.131)
(1.131) (1.132)
(1.132)
 (1.133)
(1.133) (1.134)
(1.134)
 (1.135)
(1.135)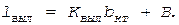 (1.136)
(1.136) (1.137)
(1.137)

 определяют в зависимости от шага обмотки.
определяют в зависимости от шага обмотки.
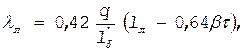 (1.154)
(1.154) ;
; .
. (1.155)
(1.155) (1.156)
(1.156)


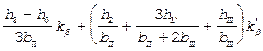



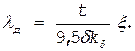 (1.157)
(1.157)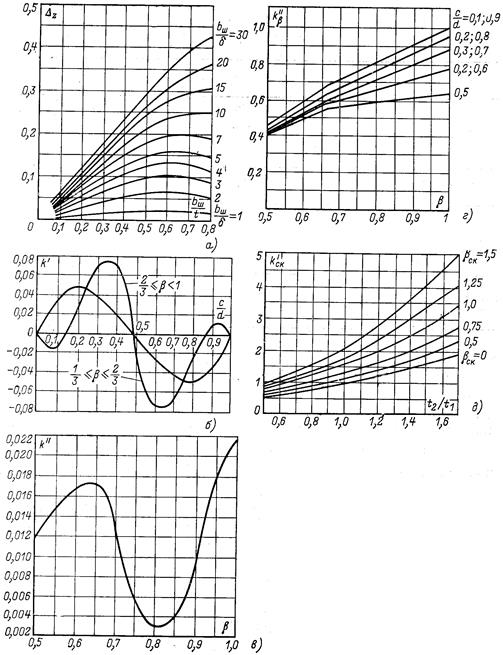
 в зависимости от укорочения шага обмотки b и дробной части числа q; д - коэффициент
в зависимости от укорочения шага обмотки b и дробной части числа q; д - коэффициент  в зависимости от соотношения t 2/ t 1 и относительного скоса пазов bСК
в зависимости от соотношения t 2/ t 1 и относительного скоса пазов bСК (1.158)
(1.158)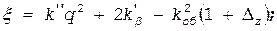 (1.159)
(1.159)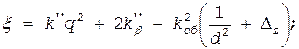 (1.160)
(1.160) (1.161)
(1.161) определяются по кривым, приведенным на рис. 1.39. Для определения
определяются по кривым, приведенным на рис. 1.39. Для определения  (1.163)
(1.163)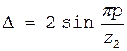 (см.§ 1.7), из (1.163) получаем:
(см.§ 1.7), из (1.163) получаем: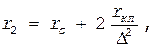 (1.164)
(1.164)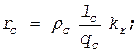 (1.165)
(1.165) (1.166)
(1.166) (1.169)
(1.169)
 (1.170)
(1.170) (1.171)
(1.171) (1.172)
(1.172) определяют по кривым рис. 1.39, д в зависимости от t2 / t1 и bск (при отсутствии скоса пазов — по кривой, соответствующей bск =0).
определяют по кривым рис. 1.39, д в зависимости от t2 / t1 и bск (при отсутствии скоса пазов — по кривой, соответствующей bск =0).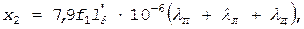 (1.173)
(1.173)
 (1.174)
(1.174) (1.175)
(1.175)
 (1.176)
(1.176) (1.177)
(1.177) по (1.156).
по (1.156). (1.178)
(1.178) ,так как активные потери в стали определяются активной составляющей тока холостого хода I0а. Из схемы замещения
,так как активные потери в стали определяются активной составляющей тока холостого хода I0а. Из схемы замещения  где
где 




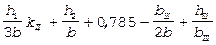


 (1.179)
(1.179) (1.180)
(1.180)
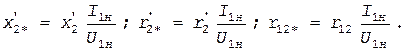
 *=0,1…0,16.
*=0,1…0,16. »0,02…0,03.
»0,02…0,03. (1.181)
(1.181)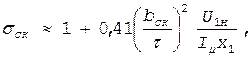 (1.182)
(1.182) (1.183)
(1.183) (1.184)
(1.184) (1.185)
(1.185)
 (1.187)
(1.187)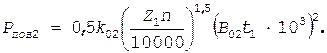 (1.188)
(1.188) (1.189)
(1.189) (1.190)
(1.190) (1.191)
(1.191) (1.192)
(1.192) (1.193)
(1.193) (1.194)
(1.194) , индекс 2 — при расчете
, индекс 2 — при расчете  .
. (1.195)
(1.195) (1.196)
(1.196) (1.197)
(1.197)
 (1.198)
(1.198) (1.199)
(1.199) (1.200)
(1.200) (1.202)
(1.202) (1.203)
(1.203) (1.204)
(1.204) (1.205)
(1.205) (1.206)
(1.206) (1.207)
(1.207) (1.208)
(1.208) (1.210)
(1.210)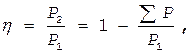 (1.211)
(1.211)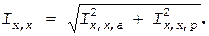 (1.212)
(1.212) (1.213)
(1.213) (1.214)
(1.214)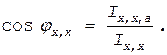 (1.215)
(1.215)


