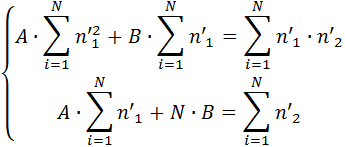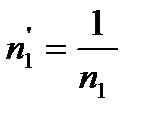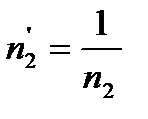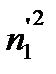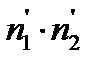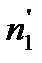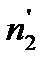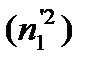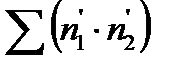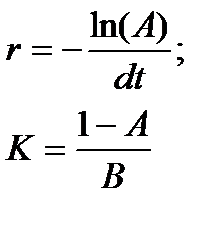Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные модели роста численности популяций.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Оглавление Введение. 4 Основные модели роста численности популяций. 4 Демографические таблицы популяций. 18 Расчет компонент сбалансированного техноценоза. 23 Зонирование территории по степени поврежденности экосистем. 27 Расчет рассеивания выбросов в атмосфере по методике ОНД-86. Определение норматива ПДВ и необходимой степени очистки выбросов. 34 Расчет платы за загрязнение атмосферы.. 41 Расчет платы за загрязнение водных объектов. 46 Организация системы мониторинга заданного объекта. 49 Расчет материального баланса веществ при сжигании твердого топлива. 56 Расчет разбавления вредных примесей по методу В.А. Фролова - И.Д. Родзиллера. Определение норматива НДС и необходимой эффективности работы очистных сооружений. 60 Расчет кислородного баланса водоема. Модель Стритера-Фелпса. 64 Список литературы.. 68
Вопросы природопользования и природообустройства являются неотъемлемой частью жизни современного общества. Человечество оказывает все возрастающее воздействие на природные экосистемы и способствует повсеместному истощению природноресурсного потенциала. Это приводит к необходимости активных мер по охране окружающей среды и обеспечению рационального природопользования. Неотъемлемой частью рационального природопользования является оценка природноресурсного потенциала территорий и текущего состояния экосистем. Настоящие методические указания призваны помочь в освоении основных подходов к обеспечению рационального природопользования, в овладении наиболее востребованных приемов природообустройства.
Занятие 1 КОНТРОЛЬНОЕ ЗАДАНИЕ. 1. По данным о численности мирового народонаселения, приведенным в табл.1.4 определить характеристики гиперболической кривой, описывающей этот рост. Таблица 1.4 ЧИСЛЕННОСТЬ МИРОВОГО НАРОДОНАСЕЛЕНИЯ
2. Определить массу зерна, которую необходимо положить на последнюю клетку шахматной доски, если, начиная с одного зернышка на первой клетке на каждую следующую кладется в два раза большее число зерен. Вес одного зерна принять равным 0.1 г.
3. Определить время, за которое потомство одной бактерии, размножающейся делением и весом 10-12 г. достигнет веса Земного шара - 1028 г., если одно деление происходит с интервалом в 20 минут.
4. Экспоненциально растущая популяция эксплуатируется в стационарном режиме, необходимо увеличить снимаемый с нее урожай в «к» раз за время «t». Определить, при каких «t» возможно увеличение урожая в «к» раз.
5. Популяция эксплуатируется в режиме на уничтожение.Определить время, за которое численность популяции сократится до 10% от первоначальной, см. табл.1.4.
Таблица 1.4 Исходные данные для выполнения контрольного задания по вариантам
6. Площадь лесов планеты составляет приблизительно 3.85 млрд. га. С учетом процессов искусственного и естественного возобновления скорость сведения лесов составляет 20 га/мин. Определить время, за которое площадь лесов сократится до 10% от первоначальной, предполагая, что их сведение происходит по экспоненте.
7. По данным таблиц хода роста древостоев основных лесообразующих пород начиная с возраста 60 лет и старше определить их популяционные параметры приняв в качестве закона роста J - образную кривую. cм.табл.1.5.
8. По данным таблиц хода роста основных лесообразующих пород определить их популяционные параметры приняв в качестве закона роста модифицированный логистический. Использовать данные о ходе роста по запасу. cм.табл.1.5.
Таблица 1.5. ХОД РОСТА ОСНОВНЫХ ЛЕСООБРАЗУЮЩИХ ПОРОД, м3/га.
Занятие 2 Занятие 3. Занятие 4. Указания к решению задачи По каждому из двух исходных направлений рассчитать сумму индексов состояния растительности По формуле 4.3 рассчитать плотности поврежденной растительности По формуле 4.4 рассчитать энтропию распределения поврежденной растительности H на каждом из двух исходных градиентов. По формуле 4.5 для каждого из двух исходных градиентов рассчитать среднее расстояние R до всех поврежденных особей. Повторяемость ветров с подставлять в формулу в долях единицы, а не в процентах. По формуле 4.10 рассчитать параметр f для каждого из двух исходных градиентов. По формуле 4.11 рассчитать параметр f для оставшихся шести градиентов.Расчет следует производить на основе ближайших градиентов. Например, для первого варианта расчет северо-восточного градиента правильней производить на основе данных по северному градиенту, а не по юго-западному. На основе уравнения 4.8 определить значение параметра d. Значения параметра d по искомым градиентам может немного различаться в зависимости от того, какой из двух исходных градиентов был выбран ранее за основу для расчета параметра f по тому или иному градиенту. Для каждого из шести искомых градиентов определить расстояния ri от источника промвыбросов до точек, на которых будет рассчитываться плотность поврежденной растительности и количество этих точек. Выбор расстояний производится в определенной мере произвольно. При определении значений расстояний руководствоваться расстояниями до точек, используемыми в исходных данных. Шаг расстояния увеличивается по мере удаления от источника. Из уравнения 4.7 определить статистическую сумму распределения Z для всех градиентов Из уравнения 4.7 определить плотность поврежденной растительности на каждом выбранном ранее расстоянии по каждому из шести искомых градиентов. По уравнению 4.12 определить расстояния На листе масштабно-координатной бумаги нанести значения плотности повреждения на каждом градиенте в пространственно-ориентированной системе, соблюдая масштаб расстояний. Отметить границы зон сильного, среднего и слабого повреждения. Полученные точки соединить прямыми линиями и вычислить площади соответствующих зон.
Рис. 4.1. Пример определения размеров площадей зон повреждения
Занятие 5 Занятие 6. Работа 7 Работа 8 Занятие 9 Задание 10 Занятие 11 КОНТРОЛЬНОЕ ЗАДАНИЕ 1. При заданных параметрах модели определить Xmax, Dmax, tmax. Таблица 11.3. Исходные данные для выполнения контрольного задания
2. При заданных постоянных реаэрации (k1) и скорости окисления (k2) примесей (см. таблицу) определить максимально допустимую величину БПК в зоне загрязнения (Lo) такую, чтобы минимальная концентрация кислорода в любом месте реки составляла с=6 мг/л. Положить равновесную концентрацию кислорода в воде при отсутствии загрязнений - co=9.8 мг/л.
Список литературы 1. Федеральный закон «Об охране атмосферного воздуха» №96-ФЗ. 1999г. 2. Постановление Правительства РФ №461. 2000 г. «Правила разработки и утверждения нормативов образования отходов и лимитов на их размещение». 3. Агаханянц П.Ф. Средства и методы контроля состояния окружающей природной среды: Учебное пособие/СПбГИЭУ.-СПб.:СПбГИЭУ,2011.-167 с. ПК 4. СанПиН 2.1.4.1074-01 - Гигиенические нормативы содержания вредных веществ в питьевой воде. 5. Закон «Об охране окружающей среды» М. 2002г 6. Закон «Об экологической экспертизе», М. 1995г. 7. Алексеев А.С. Мониторинг лесных экосистем. 2-изд. СПб., 2003. 116 с. 8. Методика расчета концентраций в атмосферном воздухе вредных веществ, содержащихся в выбросах предприятий. ОНД – 86. – Л.: Гидрометеоиздат, 1987. – 94 с. 9. Озерова Е.М.Оценка и прогнозирование состояния окружающей среды:Конспект лекций для специальности 080502/4 Экономика и управление на предприятии природопользования. СПб:СПбГИЭУ, 2011 – 83 с. 10. Алексеев А.С. Математические модели и методы в лесном хозяйстве. Л.: ЛТА, 1988, 88 с. Оглавление Введение. 4 Основные модели роста численности популяций. 4 Демографические таблицы популяций. 18 Расчет компонент сбалансированного техноценоза. 23 Зонирование территории по степени поврежденности экосистем. 27 Расчет рассеивания выбросов в атмосфере по методике ОНД-86. Определение норматива ПДВ и необходимой степени очистки выбросов. 34 Расчет платы за загрязнение атмосферы.. 41 Расчет платы за загрязнение водных объектов. 46 Организация системы мониторинга заданного объекта. 49 Расчет материального баланса веществ при сжигании твердого топлива. 56 Расчет разбавления вредных примесей по методу В.А. Фролова - И.Д. Родзиллера. Определение норматива НДС и необходимой эффективности работы очистных сооружений. 60 Расчет кислородного баланса водоема. Модель Стритера-Фелпса. 64 Список литературы.. 68
Вопросы природопользования и природообустройства являются неотъемлемой частью жизни современного общества. Человечество оказывает все возрастающее воздействие на природные экосистемы и способствует повсеместному истощению природноресурсного потенциала. Это приводит к необходимости активных мер по охране окружающей среды и обеспечению рационального природопользования. Неотъемлемой частью рационального природопользования является оценка природноресурсного потенциала территорий и текущего состояния экосистем. Настоящие методические указания призваны помочь в освоении основных подходов к обеспечению рационального природопользования, в овладении наиболее востребованных приемов природообустройства.
Занятие 1 Основные модели роста численности популяций. Типичным объектом природопользования являются популяции. Важнейшим параметром популяции является скорость увеличения численности. Скорость роста популяции является важной характеристикой, определяющей допустимую интенсивность эксплуатации популяции. Следовательно, скорость роста популяции представляет большой интерес в природопользовании. Популяцией называется совокупность особей одного биологического вида длительное время проживающих на данной территории и взаимодействующих между собой. Одним из наиболее важных с точки зрения интенсивности эксплуатации параметров популяции является ее численность. Численность популяций подвержена изменениям. Она может увеличиваться в благоприятных условиях и снижаться в экстремальных. Рассмотрим характер увеличения численности у молодой растущей популяции. Увеличение численности такой популяции можно описывать различными математическими функциями. В зависимости от того, какая из функций лучше всего описывает характер изменения числа особей в популяции, типу роста присваивают название. Название, как правило, соответствует названию этой функции. Рассмотрим основные, наиболее часто используемые для описания роста популяций закономерности, каковыми являются гиперболическая, экспоненциальная, J - образная и логистическая (S - образная).
1. Гиперболический рост. Графически изменение численности популяции по гиперболе описывается графиком, изображенным на рис. 1.1.
Динамика роста популяции по гиперболе описывается следующим уравнением:
его решение имеет вид:
где n - численность популяции, t* - момент времени, при котором численность популяции становится равной бесконечно большой величине, а – константа. Гиперболический рост описывает взрывоподобное увеличение численности народонаселения. Параметры гиперболической кривой и особенно интересная величина t* могут быть определены с помощью линейного соотношения (1.2) по данным о ходе роста численности популяции методом наименьших квадратов или графически. Метод наименьших квадратов заключается в нахождении таких коэффициентов уравнения, при которых сумма квадратов отклонений расчетных значений числа особей от экспериментальных данных была бы минимальной. Для применения метода наименьших квадратов необходимо вначале линеаризовать имеющуюся функцию. Для этого введем новые обозначения:
Пусть
Тогда исходная функция примет следующий вид:
Введем функцию
Это условие выполняется в тех точках, где частные производные этой функции по искомым коэффициентам обращаются в ноль:
где N – число замеров численности особей в популяции. Решая полученную систему уравнений любым доступным методом, можно вычислить коэффициенты "а" и "b" При решении системы уравнений полезно составить следующую таблицу: Таблица 1.1. Форма таблицы для решения системы уравнений (для примера по первому варианту, описанного в задании)
2. Экспоненциальный рост. Уравнение, описывающее изменение численности популяции имеет следующий вид:
его решение имеет следующий вид:
Здесь: r – биотический потенциал популяции, n0 - начальная численность. Биотический потенциал - величина, характеризующая на какую долю от общего количества изменяется численность популяции в единицу времени. Вид кривой, описывающий экспоненциальный рост, представлен на рис. 1.2.
Для экспоненциально растущей популяции важной характеристикой является время удвоения ее численности – T.
при
t = Т
Подставляя это выражение в (1.5) и логарифмируя получаем
откуда получаем выражение (1.8)
с учетом (1.8) выражение (1.5) принимает следующий вид (1.9):
где t/T – число удвоений численности популяции, произошедшее за время t. Параметры экспоненциальной кривой могут быть определены с помощью соотношения (1.5), представленного в логарифмической форме, графически или с помощью метода наименьших квадратов. Многие популяции, растущие по экспоненте, представляют хозяйственную ценность и могут активно эксплуатироваться. Процесс эксплуатации экспоненциально растущей популяции описывается с помощью коэффициента промысловой смертности – k, характеризующего интенсивность изъятия особей из популяции.
В зависимости от соотношения биотического потенциала и промысловой смертности различают три основных режима эксплуатации популяций: щадящий, стационарный и на уничтожение.
3. Рост с ограничением или J - образный. Уравнение, описывающее рост популяции по J-образной кривой, имеет следующий вид
его решение:
Где: К – максимально возможная численность популяции, т.е. емкость среды обитания. Для того чтобы данное интегральное выражение можно было решить методом наименьших квадратов, его необходимо линеаризовать. Для этого введем следующие новые обозначения:
Подставив последние выражения в (1.12) можно получить следующее линейное рекуррентное соотношение между соседними значениями численности популяции, отстоящими друг от друга во времени на величину dt:
где Для определения констант А и В применим к полученному линейному выражению метод наименьших квадратов, описанный выше:
Таблица 1.2. Форма таблицы для решения системы уравненийJ-образного роста (на примере первого варианта)
Решая систему (1.14) получаем значения А и В. После чего не составляет труда определить параметры J - образной кривой:
Величина dt=10 для всех вариантов. Таким образом, биотический потенциал и емкость среды обитания для популяции растущей по типу роста с ограничением могут быть определены по данным о ее численности в смежные равноотстоящие друг от друга моменты времени. График, описывающий рост с ограничением имеет следующий вид (рис. 1.4):
4. Логистический или S - образный рост. В этом случае уравнение, описывающее рост популяции имеет вид:
из последнего выражения находим аналогичное (1.13) линейное рекуррентное соотношение, но для величин обратных численностям популяции в смежные моменты времени: для этого выражение (1.17) необходимо видоизменить:
введем новые обозначения:
тогда:
Для решения системы уравнений 1.20 полезно использовать таблицу 1.3
Таблица 1.3. Форма таблицы для решения системы уравнений (1.20) логистического роста. (на примере первого варианта)
С помощью выражения (1.20) по данным о численности популяции в смежные равноотстоящие моменты времени могут быть определены ее биотический потенциал и емкость среды обитания. Принцип решения системы уравнений (1.20) аналогичен рассмотренному выше для гиперболического типа роста.
Величина dt=10 для всех вариантов. График, описывающий логистический рост имеет следующий вид (рис. 1.5):
Как видно из приводимого графика, на S образной кривой выделяют три участка: I - начальная стадия. Отличается низкой скоростью роста численности популяции. Это обусловлено низкой плотностью популяции, вследствие чего особи противоположного пола встречаются достаточно редко. II - стадия максимального роста. Высокая скорость увеличения численности популяции связана с тем, что плотность популяции уже достаточно велика, но пищевые ресурсы еще не являются сдерживающим фактором, т.е. емкость среды еще не достигнута. III - стадия замедления. Отличается замедлением скорости роста числа особей в популяции. Это связано с тем, что ресурсов среды обитания становится недостаточно для обеспечения всех особей. Оценка параметров логистического закона в этом случае может быть осуществлена с помощью соотношения (1.20) или другим специальным методом.
КОНТРОЛЬНОЕ ЗАДАНИЕ. 1. По данным о численности мирового народонаселения, приведенным в табл.1.4 определить характеристики гиперболической кривой, описывающей этот рост. Таблица 1.4 ЧИСЛЕННОСТЬ МИРОВОГО НАРОДОНАСЕЛЕНИЯ
2. Определить массу зерна, которую необходимо положить на последнюю клетку шахматной доски, если, начиная с одного зернышка на первой клетке на каждую следующую кладется в два раза большее число зерен. Вес одного зерна принять равным 0.1 г.
3. Определить время, за которое потомство одной бактерии, размножающейся делением и весом 10-12 г. достигнет веса Земного шара - 1028 г., если одно деление происходит с интервалом в 20 минут.
4. Экспоненциально растущая популяция эксплуатируется в стационарном режиме, необходимо увеличить снимаемый с нее урожай в «к» раз за время «t». Определить, при каких «t» возможно увеличение урожая в «к» раз.
5. Популяция эксплуатируется в режиме на уничтожение.Определить время, за которое численность популяции сократится до 10% от первоначальной, см. табл.1.4.
Таблица 1.4 Исходные данные для выполнения контрольного задания по вариантам
6. Площадь лесов планеты составляет приблизительно 3.85 млрд. га. С учетом процессов искусственного и естественного возобновления скорость сведения лесов составляет 20 га/мин. Определить время, за которое площадь лесов сократится до 10% от первоначальной, предполагая, что их сведение происходит по экспоненте.
7. По данным таблиц хода роста древостоев основных лесообразующих пород начиная с возраста 60 лет и старше определить их популяционные параметры приняв в качестве закона роста J - образную кривую. cм.табл.1.5.
8. По данным таблиц хода роста основных лесообразующих пород определить их популяционные параметры приняв в качестве закона роста модифицированный логистический. Использовать данные о ходе роста по запасу. cм.табл.1.5.
Таблица 1.5. ХОД РОСТА ОСНОВНЫХ ЛЕСООБРАЗУЮЩИХ ПОРОД, м3/га.
Занятие 2
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 566; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.141 (0.015 с.) |


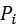 на каждом из расстоянийri по двум исходным направлениям
на каждом из расстоянийri по двум исходным направлениям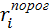 от источника загрязнения, на которых располагаются границы зоны сильных повреждений (
от источника загрязнения, на которых располагаются границы зоны сильных повреждений ( , зоны средних повреждений (
, зоны средних повреждений ( и зоны слабых повреждений (
и зоны слабых повреждений (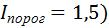 по всем восьми градиентам.
по всем восьми градиентам.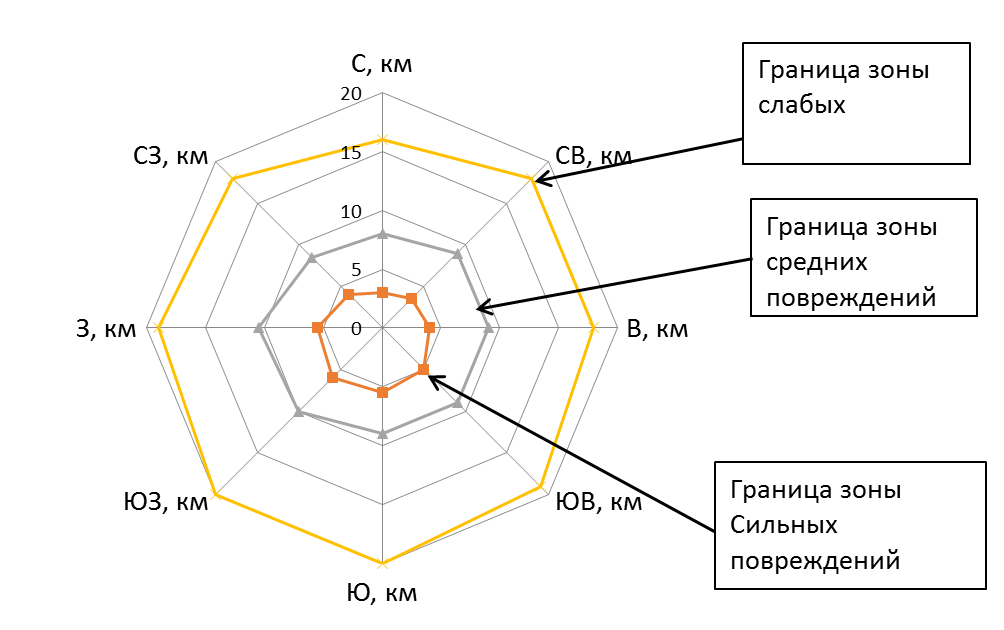
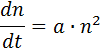
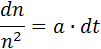
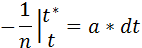
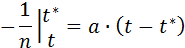
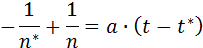
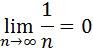
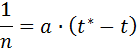
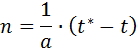
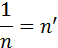
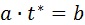
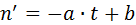
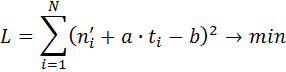
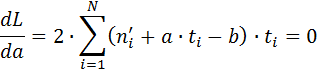
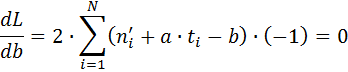
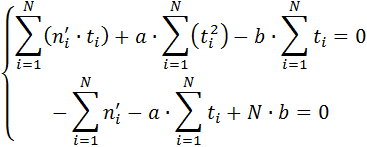
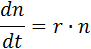

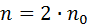
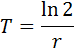
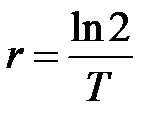 (1.8)
(1.8)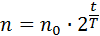
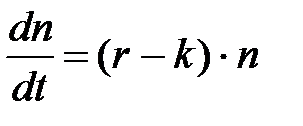
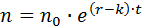
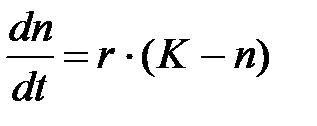 (1.11)
(1.11)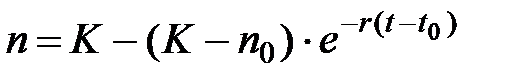 (1.12)
(1.12)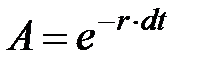
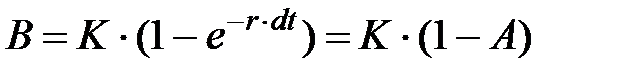
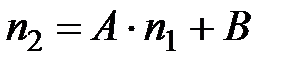 (1.13)
(1.13) и
и  - численности популяции в два смежных, отстоящих друг от друга на величину времени dt момента времени.
- численности популяции в два смежных, отстоящих друг от друга на величину времени dt момента времени.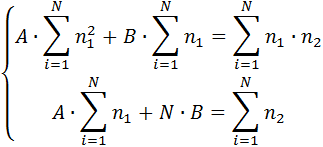
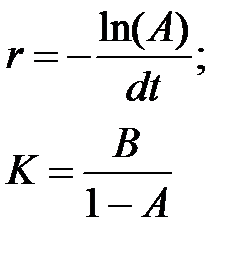 (1.15)
(1.15)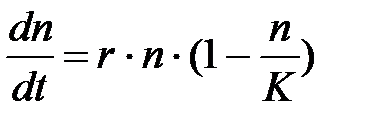 (1.16)
(1.16)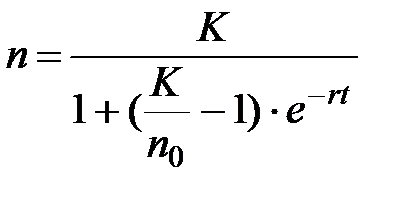 (1.17)
(1.17)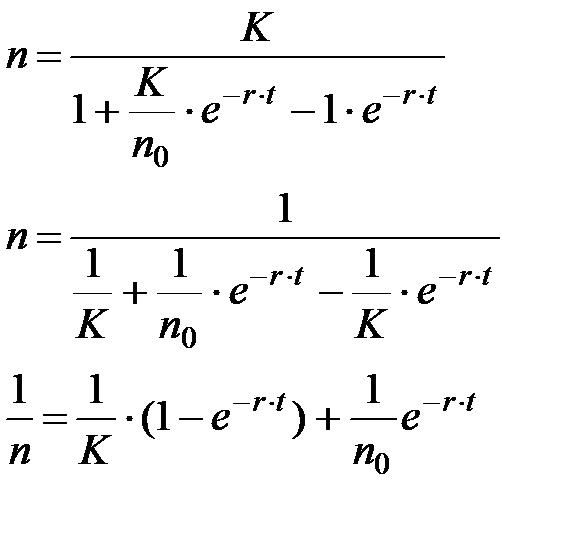
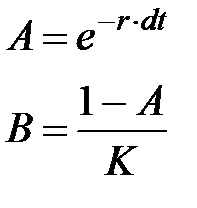
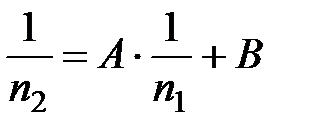 (1.18)
(1.18)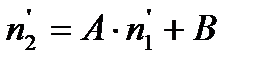 (1.19)
(1.19)