
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет однопролетного балочного перехода с компенсатором статически определимой системыСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Оптимальной является конструкция, в которой максимальный изгибающий момент в середине пролета
Выровняем моменты в прогибе и на опорах:
Тогда максимальный допустимый пролет
где
Допустимые напряжения изгиба определим, используя условия прочности для надземных трубопроводов, приведенное в СНиП 2.05.06 – 85:
Учитывая, что продольные деформации практически свободно реализуются за счет компенсаторов (трением трубопровода на опорах пренебрегаем):
Продольные напряжения от действий внутреннего давления являются растягивающими, следовательно, продольные усилия в трубопроводе
Таким образом, при пластической работе металла:
Тогда максимальная длина однопролетного двухконсольного перехода с компенсаторами будет равна:
а по условию задания
Вывод: т.к. максимальная длина однопролетного двухнонсольного перехода с компенсатором составляет 73,13 м, а ширина препятствия 152 м, то перекрыть препятствие однопролетным балочным переходом с компенсатором невозможно.
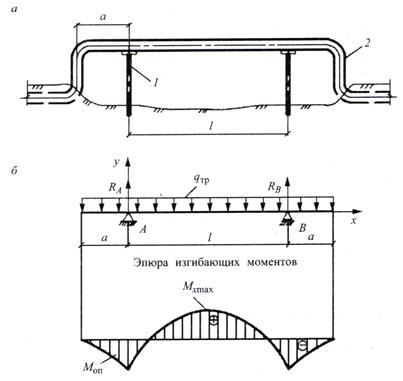
Рис. 2. Однопролетный балочный переход с компенсацией продольных деформаций: a – конструкция перехода; б – расчетная схема; 1 – опора; 2- компенсатор
Расчет многопролетного балочного перехода с компенсатором Статически неопределимой системы
Максимальный изгибающий момент в середине крайних пролетов и момент на крайних опорах равны между собой по абсолютной величине при длине консоли
Тогда длина пролета будет равна:
Так как длина перехода п = 3,
Получаем 4 пролета и 3 опоры.
Максимальный прогиб в середине пролета:
Выравниваем изгибающие моменты только на опорах:
Максимальный изгибающий момент в пролете и изгибающий момент на опоре рассчитываются, соответственно, по формулам:
Расчет нагрузок на опоры балочных переходов с компенсаторами
Расчет нагрузок, действующих на опоры многопролетного балочного перехода, выполняется аналогично расчету нагрузок, действующих на опоры однопролетного балочного перехода. Нагрузки на опоры:
- вертикальная составляющая:
- горизонтальная составляющая: - поперечная - продольная где
В зависимости от вида опор, коэффициент трения может принимать следующие значения: 1) при скользящих опорах при трении стали о сталь 2) при катковых опорах
Таким образом, 1) при скользящих опорах при трении стали о сталь: принимаем
2) при катковых опорах: принимаем
Расчет компенсаторов
Наибольшее распространение в конструкциях балочных переходов получили Г-образные компенсаторы. Расчетные продольные напряжения изгиба в компенсаторе, вызванные изменением длины надземного участка трубопровода, максимальны в точке защемления и определяются по формуле из СНиП 2.05.06-85*:
где
Максимально допустимые напряжения
где В наклонных компенсаторах, не являющихся одновременно опорами, напряжения
Таким образом,
При заданной рабочей длине компенсатора
Если же известно суммарное продольное перемещение трубопровода
При продольном перемещении трубопровода за счет его удлинения максимальная величина
где
Таким образом,
В случае уменьшения длины трубопровода величина ∆к будет максимальной при внутреннем давлении
где Таким образом,
Амплитуда отклонения начальной длины в обе стороны:
Таким образом,
Вывод: номинальная длина компенсатора с учетом максимально допустимого напряжения составляет 13,65 м. Наиболее оптимальным, с точки зрения строительной механики, является выполнение многопролетного перехода с компенсацией продольных деформаций. Заключение
В ходе выполненного курсового проекта было произведено ознакомление с расчетом одно- и многопролетных балочных переходов с компенсацией продольных деформаций и без компенсации. Основываясь на произведенном расчете были получены следующие данные: при строительстве перехода без использования компенсатора необходимо задействовать 4 пролета по 45,79 м для того, чтобы перекрыть препятствие в размере 152м, а при использовании компенсатора будет достаточно двух пролетов, длинной по 72,13 м, что более оптимально и менее затратно.
Список литературы:
1. Беляев Н.М. Сопротивление материалов – М: Главная редакция физико-математической литературы издательства «Наука», 1976 г. – С. 342-376 2. СНиП 2.05.06-85*. Магистральные трубопроводы/Госстрой СССР. –М.:ЦИТП Госстроя СССР, 1985 -71 с. 3. СНиП 2.01.07-85*. Нагрузка и воздействия/Госстрой СССР. –М.:ЦИТП Госстроя СССР, 1986 – 47 с.
|
||||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.007 с.) |

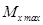 и момент на опоре
и момент на опоре  равны по абсолютной величине.
равны по абсолютной величине.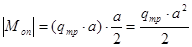
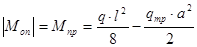
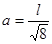
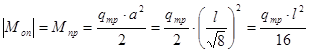
 из условия прочности определяется по формуле:
из условия прочности определяется по формуле: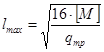 ,
,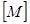 - допустимый изгибающий момент в трубопроводе, равный
- допустимый изгибающий момент в трубопроводе, равный 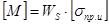 .
. .
. ,
, 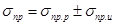 .
.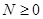 и
и  =1.
=1. ,
, .
.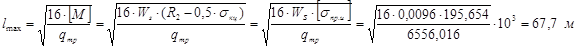 (6.1)
(6.1)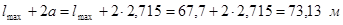 , (6.2)
, (6.2)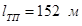 .
.
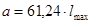 .
.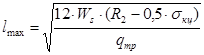 ,
,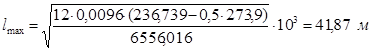 (7.1)
(7.1) , а длина перекрываемого пролета
, а длина перекрываемого пролета 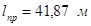 , т.е.
, т.е.  , то для достижения устойчивости необходимо установить 3 дополнительные опор:
, то для достижения устойчивости необходимо установить 3 дополнительные опор: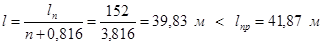 . (7.2)
. (7.2)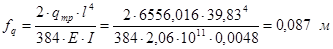 . (7.3)
. (7.3)
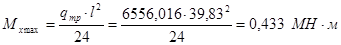 ; (7.4)
; (7.4)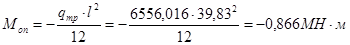 . (7.5)
. (7.5) ; (8.1)
; (8.1)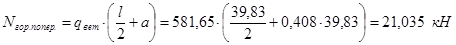 (8.2)
(8.2) ,
,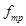 – коэффициент трения.
– коэффициент трения.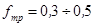 ;
; , где
, где 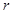 – радиус катка, см;
– радиус катка, см;
 ; (8.3)
; (8.3)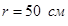 ,
,  ;
; . (8.4)
. (8.4)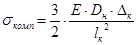
 – вылет компенсатора (рабочая длина компенсатора);
– вылет компенсатора (рабочая длина компенсатора); – суммарное продольное перемещение трубопровода в месте примыкания его к компенсатору от воздействия температуры и внутреннего давления.
– суммарное продольное перемещение трубопровода в месте примыкания его к компенсатору от воздействия температуры и внутреннего давления.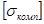 можно определить из условия прочности:
можно определить из условия прочности:
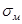 – дополнительные продольные напряжения в компенсаторе от изгиба под действием поперечных и продольных нагрузок (усилий) в расчетном сечении компенсатора, определяемые согласно общим правилам строительной механики.
– дополнительные продольные напряжения в компенсаторе от изгиба под действием поперечных и продольных нагрузок (усилий) в расчетном сечении компенсатора, определяемые согласно общим правилам строительной механики. . (9.1)
. (9.1) , называемую компенсирующей способностью компенсатора:
, называемую компенсирующей способностью компенсатора:
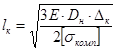
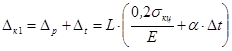
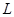 – длина надземного участка трубопровода, обслуживаемая одним компенсатором;
– длина надземного участка трубопровода, обслуживаемая одним компенсатором;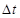 – перепад температур при нагревании.
– перепад температур при нагревании. .(9.2)
.(9.2) .
.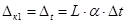 ,
,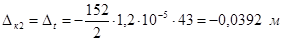 . (9.3)
. (9.3) . (9.4)
. (9.4)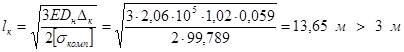 .(9.5)
.(9.5)


