
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Расчет балочных переходов без компенсации продольных деформацийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Условие прочности при пластической работе металла:
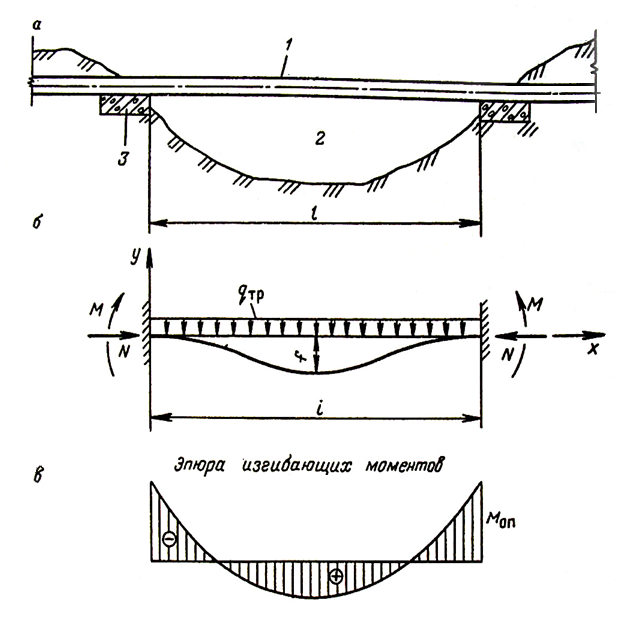
Находим максимальный изгибающий момент в сечении балки, для этого строим эпюру изгибающих моментов нарезной балки с защемленными концами нагруженную равномерно распределенной нагрузкой qтр и длинной пролета l:
Рис. 1. Однопролетный балочный переход без компенсации продольный деформаций.
а – конструкция перехода б – расчетная схема в – эпюра изгибающих моментов 1 – трубопровод 2 – овраг 3 – опорная плита Вместо защемленных концов справа и слева добавляем по пролету, длина которых равна нулю, и таким образом, переходим к расчету шарнирно-опертой нарезной балки. В соответствии с теоремой о трех моментах: По правилам строительной механики статически неопределимой системы получаем:
1) При известной полной расчетной нагрузке
Так как длина перехода п = 2, п = 3, п = 4,
Таким образом, получаем 4 пролетов и 3 дополнительных опор 2) Соответствующая стрела прогиба, вызванная расчетной нагрузкой
3) Продольное усилие, действующее в трубопроводе:
При ∆t ≤ 0 усилие N положительно (растягивающее), при ∆t ≥ 0 оно может быть как положительным, так и отрицательным (сжимающим). При
При
4) Критическая (Эйлерова) сила:
где
При 5) Коэффициент ξ При
При 6) Фактическая стрела прогиба:
При ξ>0, когда усилие N отрицательно (сжимающее), фактическая стрела прогиба под действием этого усилия увеличивается по отношению к При ξ<0, когда усилие N положительно (растягивающее), фактическая стрела прогиба под действием этого усилия уменьшается по отношению к При
При
7) Изгибающий момент в наиболее напряженном опорном сечении от действия расчетной нагрузки
8) Изгибающий момент от действия продольной силы:
При
При
9) Суммарный изгибающий момент:
При
При
При отрицательном значении усилия N момент М представляет по величине сумму М1 и М2, при положительном значении – разность этих моментов. 10) Продольные напряжения:
При
При
11) Проверка прочности трубопровода в продольном направлении: Где Т.к.
Где при
При
При
Условие прочности выполняется. Вывод: препятствие шириной 152 м можно перекрыть 4 пролетным балочным переходом без компенсации продольных деформаций, но так как в расчетах принималось y3, вместо y4, а в соответствии со СНиП 2.05.06 – 85* (п.п. 8.35, примечание 2) для надземных безкомпенсаторных переходов допускается принимать y3, вместо y4, при числе пролетов не более четырех, то балочный переход рассчитывается с компенсацией продольных деформаций.
Расчет нагрузок на опоры многопролетного балочного перехода без компенсации продольных деформаций
1) Нагрузка на опоры. Вертикальная составляющая:
Горизонтальная составляющая:
где
Расчетные значения сжимающих или растягивающих напряжений
Откуда
Расчетные значения растягивающих напряжений
|
|||||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 1103; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.186 (0.009 с.) |

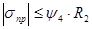
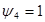
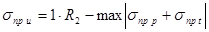
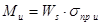
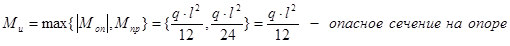
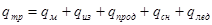 определяется длина перекрываемого пролета
определяется длина перекрываемого пролета 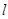 по формуле:
по формуле: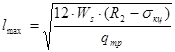
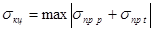
 ,(4.1)
,(4.1)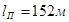 , а длина перекрываемого пролета
, а длина перекрываемого пролета 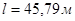 , то для достижения устойчивости необходимо установить дополнительные опоры:
, то для достижения устойчивости необходимо установить дополнительные опоры: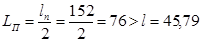 . (4.2)
. (4.2)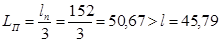 . (4.3)
. (4.3)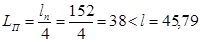 . (4.4)
. (4.4)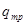 :
: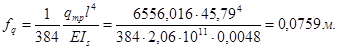 (4.5)
(4.5)
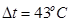
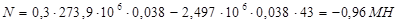 (4.6)
(4.6)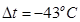
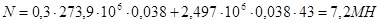 (4.7)
(4.7)
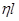 – свободная длина рассчитываемого перехода. При одном пролете
– свободная длина рассчитываемого перехода. При одном пролете 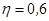 , а при двух или более
, а при двух или более 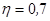 .
.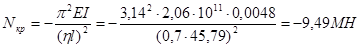 (4.8)
(4.8)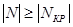 - условие выполняется.
- условие выполняется.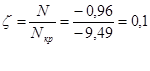 (4.9)
(4.9)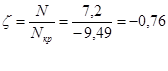 (4.10)
(4.10)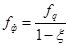 .
.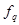 .
.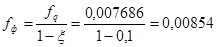 (4.11)
(4.11)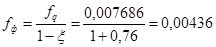 (4.12)
(4.12)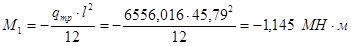 (4.13)
(4.13) ,
,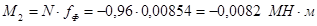 (4.14)
(4.14)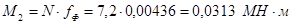 (4.15)
(4.15)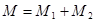 ,
,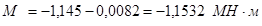 (4.16)
(4.16)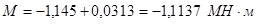 (4.17)
(4.17)
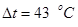
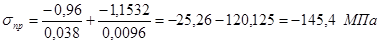 (4.18)
(4.18)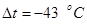
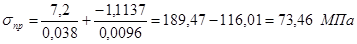 (4.19)
(4.19)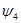 - коэффициент, учитывающий двухосное напряженное состояние трубопровода. При
- коэффициент, учитывающий двухосное напряженное состояние трубопровода. При 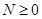 ,
, 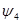 =1, при N<0
=1, при N<0 , (что не имеет физического смысла), согласно допущения в [1], вместо
, (что не имеет физического смысла), согласно допущения в [1], вместо 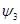
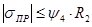 ,
,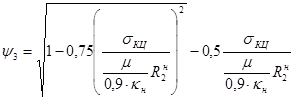 , где
, где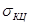 - кольцевые напряжения;
- кольцевые напряжения;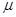 - коэффициент условия работы трубопровода, для III категории;
- коэффициент условия работы трубопровода, для III категории;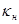 - коэффициент надежности;
- коэффициент надежности;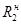 - предел текучести.
- предел текучести.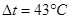 ,
,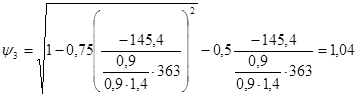 МПа, (4.20)
МПа, (4.20)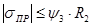 ,
,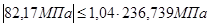 ,
,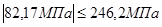 , (4.21)
, (4.21)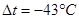 ,
, 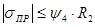 ,
,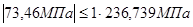 , (4.22)
, (4.22)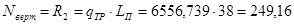 кН. (5.1)
кН. (5.1)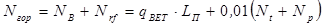 ,
,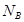 – усилие от ветровой нагрузки, действующее на опору перпендикулярно оси трубопровода;
– усилие от ветровой нагрузки, действующее на опору перпендикулярно оси трубопровода;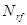 - усилие, возникающее перпендикулярно оси трубопровода вследствие отклонения от прямой линии оси;
- усилие, возникающее перпендикулярно оси трубопровода вследствие отклонения от прямой линии оси;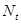 и
и  - продольные усилия в трубопроводе, возникающие от изменения температуры и внутреннего давления.
- продольные усилия в трубопроводе, возникающие от изменения температуры и внутреннего давления.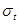 и усилия
и усилия 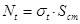 ,
, 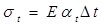 .
.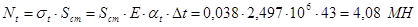 . (5.2)
. (5.2)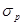 и усилия
и усилия 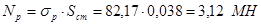 . (5.3)
. (5.3)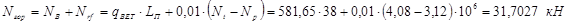 (5.4)
(5.4)


