
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Автоматизація розвязування задач оптимального вибору в процесах управлінняСодержание книги
Поиск на нашем сайте Основна задача лінійного програмування Оптимізаційною наз-ся задача, в якій необхідно знайти найбільше або найменше значення деякої величини, яка задовольняє певні умови (с-ми обмежень). Нехай потрібно знайти максимум або мінімум функції n Z=∑ci xi, де ci – числові коефіцієнти, xi –змінні. i=1 При цьому отриманий максимум або мінімум має задовольняти певну систему умов: {Ах>= (<=)b, х>=0 Така задача наз-ся задачею лінійного програмування, функція z наз-ся цільовою, а вищеназвана система – системою обмежень. Приклади задач лінійного програмування: транспортна задача, оптимізація управління обіговим капіталом, планування штатного розкладу. Розвязання ЗЛП дозволяє знайти оптимальний розвязок задачі, оптимальні значення результуючих змінних за умови виконання певних обмежень. Оптимальне планування господарської діяльності торгівельних підприємств та її розв’язування в Excel. Напр, ЗЛП стосовно діяльності торг. п-ва може звучати наступним чином: Фірма виробляє декілька видів продукції, відомі норми витрат комплектуючих на в-цтво цієї продукції і запас комплектуючих на складі. Відома також ціна на кожен вид продукції. Скільки фірмі потрібно виробити кожного виду продукції, щоб ортимати максимальний прибуток? В даному випадку цільова функція Z- максимальний прибуток, який може отримати фірма за заданих умов, а обмеження стосуються запасів комплектуючих на складі і норм витрат їх на виробництво. Х1,Х2…Хn- це оптимальна кількість виробництва кожного виду продукції, яку ми отримуємо в рез-ті розвязку задачі. В Excel і вона розв’язується за доп. пакету Аналізу, в якому міститься пункт «Поиск решения». Інші обмеження, які можуть враховуватися в ЗЛП: 1. Обмеження за трудовими ресурсами 2. Обмеження за корисною площею 3. Обмеження за зар. платою 4. Планові обмеження (прибуток від реалізації) 5. Фізичні обмеження Постановка та розв’язування транспортної ЗЛП. У сучасній економіці торгівлі велике значення мають задачі, пов’язані з транспортуванням вантажів. Транспортування товарів від пунктів виробництва до пунктів їх споживання вимагає великих витрат. Вони залежать від:відстані; схем перевезень; видів транспорту тощо. Транспортна задача – це задача вибору оптимального варіанта доставки товару від пунктів виробництва до пунктів споживання з урахуванням усіх реальних можливостей. Серед багатьох прикладів застосування транспортної задачі в торгівлі зазначимо такі: · Оптимальний розподіл торгівельної площі магазинів різних районів під групи різних товарів; · Оптимальний розподіл баз і торгівельних точок у населених пунктах тощо. Використання розрахунків транспортної задачі, як правило, знижує транспортні видатки на 10-30%. Транспортні задачі за своєю постановкою поділяються на кілька груп: Ø Задачі на мінімізацію вартості перевезень товару від пунктів виробництва до пунктів споживання; Ø Задачі на мінімізацію довжини маршруту при перевезенні вантажу від одного постачальника до кількох споживачів; Ø Задачі на мінімізацію строків перевезення товару від пунктів виробництва до пунктів споживання тощо. Приклад транспортної задачі Деяка фірма будує дорогу. Їй необхідні постачання: піску, гравію, бетону, асфальту та ін. По мірі будівництва фірма віддаляється від старих постачальників (кар’єрів, бетонних заводів, залізниці та ін.), транспортні витрати зростають. Фірма шукає нових постачальників, менеджери перераховують транспортну задачу, оцінюють витрати на перевезення матеріалів, хочуть їх мінімізувати. В загальному випадку транспортна задача полягає в тому, що необхідно доставити необхідну кількість ресурсів від розподілених в просторі постачальників до розподілених в просторі споживачів. При цьому товари можуть доставлятися з будь якого «заводу» на будь який «склад», але витрати на перевезення будуть різними. Мета розв’язання транспортної задачі: Cкласти найкращий оптимальний план перевезень від постачальників до споживачів з урахуванням обмежених ресурсів постачальників і відомими потребами споживачів. Мінімізувати витрати на перевезення. Нехай відомі: 1) Перелік споживачів j=1,m і об’єми їх потреб - 2) Перелік постачальників і =1, п і їх потужності - 3) Витрати на поставку одиниці вантажу від кожного постачальника до кожного споживача - cij; і =1, п; j =1,m. Позначимо через xij - невідомі планові кількості перевезень від i –го постачальника до j –го споживача. Тоді математична модель транспортної задачі буде такою:
де
|
||
|
Последнее изменение этой страницы: 2016-09-13; просмотров: 292; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.33 (0.01 с.) |

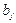 ;
;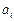 ;
; , (1)
, (1)  (2)
(2)  (3)
(3) 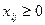 - невід’ємні об’єми перевезень, z - функція мети: мінімізація загальних витрат при перевезені товару від всіх постачальників до всіх споживачів,
- невід’ємні об’єми перевезень, z - функція мети: мінімізація загальних витрат при перевезені товару від всіх постачальників до всіх споживачів, 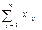 - план поставок від i –го постачальника по всім споживачам,
- план поставок від i –го постачальника по всім споживачам, 
 - план поставок j –му споживачеві від всіх постачальників. В Excel і вона розв’язується за доп. пакету Аналізу, в якому міститься пункт «Поиск решения».
- план поставок j –му споживачеві від всіх постачальників. В Excel і вона розв’язується за доп. пакету Аналізу, в якому міститься пункт «Поиск решения».


