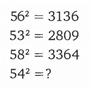Прежде нем продолжить: технике побеждает не всегда

Современные технологии сильно облегчают нам жизнь. Мы можем за долю секунды связаться с нужным человеком при помощи небольшого устройства, которое легко помещается в кармане, — а можем сегодня же провести поиск и собрать исчерпывающую информацию, всего лишь пробежавшись пальцами по клавиатуре и воспользовавшись какой-нибудь поисковой системой, например Google. Но чудесная доступность всего и вся порождает лень. Компьютеры делают за нас всю работу — даже думают иногда. Телефоны хранят для нас нужные телефонные номера, так что их даже не приходится запоминать. Калькуляторы избавляют от необходимости считать в уме или на бумажке, а специализированные программы для смартфонов подсчитывают, сколько чаевых следует оставить в ресторане. Даже искусство письма от руки, при котором задействуются творческие участки мозга, теряется и уходит, проиграв битву компьютерной клавиатуре.

У меня есть сестра, которая принципиально отказывается пользоваться ускоренным набором телефонных номеров; она не подсчитывает простые вещи на калькуляторе и никогда не включает автоматическую проверку правописания. Она даже GPS пользуется только в самых крайних случаях. Я, кстати говоря, считаю, что она очень умна и обладает блестящим и быстрым мозгом. Не знаю наверняка, откуда у нее привычка игнорировать по возможности технику, но мне кажется, что это как-то связано с нашим отцом. Когда мы были детьми, отец вместе с тремя своими братьями владел магазином готового платья, и бизнес они вели без применения техники. У них вообще не было технических устройств, никаких! Считал отец по большей части в уме, отлично помнил клиентов и вообще вел дела исключительно по памяти — хотя большинство людей на его месте пользовались бы доступной техникой. Даже когда появились компьютеры и кнопочные телефоны, он их не покупал; у него даже кассового аппарата не было! Он все держал в уме, в крайнем случае пользовался бумагой и ручкой — и старомодным дисковым телефоном. Нам с сестрой время от времени приходилось работать в магазине и наблюдать все процессы изнутри. Впечатление было довольно сильное. Сегодня, оглядываясь назад, я понимаю, что работа в магазине многому меня научила. Мой мозг приобрел навыки, которыми я пользуюсь до сих пор, хотя тогда я не догадывался, насколько все это повлияет на мое развитие.

Каждый клиент в нашей системе имел собственный номер, и я помню амбарные книги размером с телефонный справочник, в которые записывались имена клиентов и их номера. Каждый месяц отец заставлял меня добавлять к неоплаченным счетам клиентов по 1,5%, и я ненавидел заниматься этим, ведь считать приходилось без калькулятора. Я упрашивал его сдаться и завести компьютер, чтобы облегчить жизнь себе и всем нам — тем, кому приходилось корпеть над цифрами в его офисе! Но отец всегда отвечал, что такой технике не место в его магазине. Он говорил: «Если General Motors успешно работают 50 лет без компьютеров, то и я смогу!» (Замечу, что это заявление он сделал задолго до того, как GM объявила о банкротстве, — да и обанкротилась компания после того, как завела у себя компьютеры. Но оставим это без комментариев.) Сегодня я рад, что отец смог настоять на своем. Во многом своей «технологии мышления» и я, и моя сестра обязаны ему. Он показал мне, насколько мощным инструментом может быть мозг. Он также внушил мне, что если в технике нет настоятельной необходимости, ее лучше избегать, и что не следует спешить заменять наши собственные внутренние технологии новыми, внешними.

Есть время и место для всей этой техники, но есть также время и место для добрых старых методов решения задач. Позвольте мозгу работать — и вы увидите невероятные результаты. Приведу еще одну аналогию. Представьте, что вам необходимо сделать серьезную операцию на сердце. Что вы предпочтете — чтобы ее делал хирург, обучавшийся на компьютерном тренажере, или опытный врач, работавший с реальными пациентами? Я бы лично выбрал хирурга с опытом реальной работы. В этом деле необходим человек, привыкший быстро решать самые разные проблемы, неожиданно возникающие в ходе операции. Не секрет, что в процессе работы человек набирается опыта; важно также, что происходит синтез, обобщение и структуризация этого опыта, и это позволяет решать новые задачи с использованием как комбинации уже известных фактов, так и того, с чем мы столкнулись в данном случае. В повседневной жизни может хватить и книжного опыта, — а иногда техника сама сделает все за человека, — но тот, кто успел извлечь из жизненных ситуаций множество уроков, часто находит лучшее или более точное решение. Это как в самолете. Вы ведь не захотите, чтобы вашим самолетом управлял пилот, никогда не летавший по-настоящему и лишь недавно закончивший обучение на тренажерах. Гораздо спокойнее лететь с пилотом, налетавшим тысячи реальных часов в самых разных условиях.

А теперь задумайтесь, что это означает в контексте гениальности. Гении достигают высот не благодаря технике или книгам, из которых черпают знания. Конечно, они пользуются и техникой, и учебниками, но полагаются в первую очередь на собственный разум, включая ту его часть, что заставляет задавать вопросы, подвергать сомнению нормы и никогда не говорить: «Я не могу». Гении приобретают и используют «реальные» навыки, которые формируются при слиянии общих фоновых знаний и конкретного опыта; именно они позволяют им выделяться из общей массы и менять мир, адаптироваться к новым обстоятельствам и отзываться на новые потребности. Именно этому я и собираюсь вас научить.

 

 

Сила паттернов

Все дело во взаимосвязи!

Я никогда неучу своих учеников; я всего лишь пытаюсь обеспечить условия, в которых они смогут учиться.

Альберт Эйнштейн

 

Паттерны есть повсюду, куда ни посмотри. Они прячутся в числах, в словах и даже в природе. Если вы, к примеру, возьмете любой номер журнала National Geographic, то увидите там красивейшие фотографии паттернов, которые можно наблюдать среди животных, в пейзажах, цветах, звездах, россыпях песка и т. п. Большинство людей не замечает этих закономерностей, если они буквально не бросаются в глаза (как на этих фотографиях), до тех пор, пока им не дали задание отыскать их — или если они не похожи на меня и не обзавелись, как я, привычкой искать закономерности везде и всюду.

В этой главе я собираюсь представить вам увлекательный, я надеюсь, рассказ о том, как паттерны играют с нашим сознанием и как мы можем использовать их не только для тренировки мозга и особенно памяти, но и для того, чтобы рассмотреть все окружающее под совершенно иным углом; новый взгляд — отличное средство вызвать озарение, найти новые, более эффективные решения повседневных проблем, подстегнуть мысль.

Что такое паттерн?

Начнем с начала: что, собственно, такое паттерн? Слово это произошло от французского patron и обозначает просто некий шаблон, тему из повторяющихся событий или объектов. Если бы я попросил привести пример паттерна, вы, вероятно, назвали бы что-нибудь из визуальных элементов, присутствующих обычно в орнаментах и отделке; это могут быть полосы, зигзаги или узор горошком, рисунок на обоях в вашей спальне, расцветка любимых носков «ромбиками» или тонкая полоска на костюмной ткани. А может быть, вы подумали бы о паттернах в песенном ритме, о правильных чередующихся полосах слоев на скальном обнажении, об архитектурных элементах, о транспортных потоках и сигналах светофоров, об эмблемах автопроизводителей или фрагментах произведений искусства, к примеру, в работах Моне, Ван Гога и Рембрандта. Стандартные структуры (паттерны) из атомов водорода и кислорода образуют воду, паттерны замерзших кристалликов льда — снежинки, паттерны снегопада обеспечивают нам лыжню и т.д. Циклическую смену дня и ночи тоже можно назвать своего рода шаблоном, а тела наши следуют биологическим ритмам, связанным с 24-часовыми солнечными сутками. Мы редко вспоминаем о паттернах внутри себя, на самом же деле биологические закономерности в значительной мере определяют, кто мы и как себя чувствуем. У каждого из нас есть суточный цикл — биологические часы, которые 24 часа в сутки поддерживают регулярный стабильный ритм. После захода солнца мы испытываем усталость, на восходе — прилив энергии. Питается большинство людей тоже регулярно — завтрак, обед и ужин выстраиваются друг за другом по заведенному порядку. У каждого из нас есть постоянные привычки, определяемые сменой дня и ночи, сна и бодрствования; кроме того, тело, поддерживая биохимическую активность, в разные моменты суток вырабатывает разные гормоны.

И, разумеется, без паттернов невозможны компьютерные программы, язык, литература и математика, определяемая обычно как «наука о структурах, порядке и отношениях». Любая последовательность чисел, которую можно задать математической функцией, считается упорядоченной (то есть представляет собой своеобразный паттерн). Возможно, такие паттерны сложнее выявить, чем многие другие, но для тренировки ума они подходят замечательно. Рассмотрим несколько для разминки.

2,4, 6, 8, 10,___,_,__. (Можете ли вы определить недостающие числа?)

Это очень простой пример: последовательность четных чисел. А вот еще один:

77, 49, 36, 18,____. (Можете ли вы определить следующее

число?)

Вот как это действует:

Семью семь — произведение двух цифр первого числа, равное сорока девяти — это второе число в серии. Далее снова: четырежды девять равняется тридцати шести; это третье число. И далее по тому же принципу: трижды шесть будет восемнадцать; это четвертое число. Единожды восемь — восемь; это пятое недостающее число серии. Здорово, правда?

Иногда закономерности приходится искать другими, более тонкими способами. Я покажу вам несколько примеров на вычисление произведения двух чисел. Попробуйте найти закономерность в способе расчета. Может быть, сразу вы ее не увидите, поэтому не спешите. Это упражнение само по себе отлично помогает разбудить мозг.

 

Подсказка: Этот способ работает только при перемножении двух чисел от 100 до 109. Все ответы должны быть пятизначными числами.

Внимание: во многих упражнениях я при объяснении решения буду использовать такие понятия, как «цифра разряда десятков» и «цифра разряда единиц». Это помогает мне точно называть числа. Если вы нуждаетесь в пояснении, то вот оно:

В числе 123 «3» — цифра единичного разряда (число единиц), «2» — цифра разряда десятков (число десятков), и «1» — цифра разряда сотен (число сотен).

Ответ: Первая цифра результата — всегда единица. Следующие две цифры результата, или «среднее» число, находится путем сложения цифр единичного разряда в каждой задаче. Так, при перемножении 105 и 107, вы складываете 5 и 7 и получаете 12; при перемножении 102 и 104 складываете 2 и 4 и получаете 6. Но имейте в виду: в «среднем» числе должно быть две цифры, так что перед 6 придется поставить 0. При перемножении 109 и 106 вы складываете 9 и 6 и получаете 15. Наконец, чтобы получить последние две цифры результата, нужно перемножить цифры единичного разряда в каждом примере. Так, для чисел 105 и 107 вы умножаете 5 на 7 и получаете 35; для чисел 102 и 104 умножаете 2 на 4 и получаете 8. Опять же, на этом месте не может стоять одна цифра, поэтому перед восьмеркой ставим 0. Наконец, при перемножении 109 и 106 вы умножаете 9 на 6 и получаете 54.

Можете рассмотреть еще несколько аналогичных примеров. Цель этого упражнения — не столько научить вас упрощенному способу перемножения чисел от 100 до 109, сколько помочь вам заставить свой мозг обращать внимание на закономерности и проделывать всякие фокусы. (Не забывайте, все решения можно найти в конце главы.)

 

Хорошо, немного усложним задачу. Ниже вы найдете способ возведения в квадрат чисел шестого десятка. Отыщете закономерность?

 

Подсказка: Уберите 5 и поищите закономерность.

Ответ: 2916.

Решение: В каждом случае квадрат цифр единичного разряда (6², З², 8²) исходного числа дает две последние цифры ответа (36, 09 и 64 соответственно). Именно поэтому я посоветовал вам для начала убрать пятерку, чтобы легче было это заметить. Теперь нужно возвести в квадрат 5 (5²), что даст нам 25. Затем добавьте к 25 цифру единичного разряда. Так, в случае 56² у нас 25 + 6 = 31; в случае 53² прибавим 3 к 25, и получим 28; в случае 58² складываем 25 и 8, получаем 33. Давайте вычислим 54² вместе:

• Возводим в квадрат цифру единичного разряда, 4 х 4 = 16. Это две последние цифры ответа.

• Берем 5 раз по 5, получаем 25 и прибавляем цифру единичного разряда, 25 + 4 = 29. Это дает нам первые две цифры ответа.

• Ответ: 2916.

Все понятно? Если нет, вернитесь и еще раз все продумайте. Потренируйтесь. Добейтесь, чтобы это упражнение вы могли выполнять в уме быстро и легко. Вот еще примеры:

57² =______________.

55² =_____.

59² =_____.

51² =_____.

52² =_____.

Паттерны — это не обязательно сложный ряд различных цифр или других объектов. Они могут быть «проще» и представлять собой, к примеру, сложную последовательность одинаковых цифр или предметов. Первое, что приходит на ум в качестве примера, — это двоичный код. Слово «двоичный» относится к тому, что состоит из двух частей. Нам часто приходится слышать, что двоичный код — это способ представления текста или процессорных команд при помощи двух цифр двоичной системы счисления, 0 и 1. Для этого каждому символу или каждой команде ставится в соответствие так называемая бинарная (двоичная) последовательность. К примеру, двоичная последовательность из восьми цифр (бит) может представлять любое из 256 возможных значений, а потому может соответствовать множеству различных символов, букв или команд. Даже если вы не понимаете, что все это на самом деле означает, достаточно сказать, что возможностью создавать компьютеры и сложные программы для них мы в значительной мере обязаны простым комбинациям нулей и единиц.