
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Общий способ расчёта прочности железобетонных элементовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
В сечениях, перпендикулярных к продольной оси элементов, изгибаемых, внецентренно сжатых и внецентренно растянутых в стадии III двузначные эпюры напряжений в бетоне и арматуре будут одинаковые во всех трёх случаях (рис. 35).
 
На этом рисунке h0 – рабочая высота сечения, равная h - а; а и а' – расстояния от равнодействующей усилий в арматуре соответственно As и A's до ближайшей грани сечения. В расчётах прочности элементов усилия, воспринимаемые сечением, перпендикулярным к продольной оси элемента, определяют по расчётным сопротивлениям материалов (т.е. с учётом пониженной против контролируемой прочности бетона и арматуры) с учётом коэффициентов условий работы. При этом используют следующие допущения: - элемент может иметь любую симметричную относительно вертикальной оси форму поперечного сечения; силовая плоскость изгиба должна совпадать с этой осью; - элемент работает в стадии III напряжённо-деформированного состояния; - работой растянутого бетона над трещиной пренебрегаем; - для того, чтобы в сжатой арматуре A's напряжения заведомо доводились до расчётного сопротивления сжатию Rsc (при отсутствии сцепления арматуры с бетоном Rsc = 0) необходимо, чтобы равнодействующая усилий в арматуре A's отстояла от нейтральной оси дальше, чем равнодействующая усилий в бетоне сжатой зоны Db, т.е. выполнялось неравенство zb ≤ zs. Введение этих допущений позволяет получить расчётные формулы с использованием только двух уравнений равновесия. В общем случае условие прочности при любом из перечисленных выше усилий от внешних воздействий формулируется в виде требования о том, чтобы момент усилий от внешних воздействий, взятый относительно любой оси, перпендикулярной к плоскости изгиба, не превосходил суммы моментов внутренних усилий, взятых относительно той же оси. Обычно это условие записывают в виде
Уравнение равновесия (2.20) можно представить в виде условия прочности в форме:
где Sb – статический момент площади сечения бетона сжатой зоны Аb относительно той же оси, т.е. Sb = Abzb; Zb – плечо внутренней пары сил. Во внецентренно сжатых и внецентренно растянутых элементах М = Ne. Высоту сжатой зоны х для сечений, работающих по случаю 1, определяют из уравнения равновесия расчётных усилий на продольную ось элемента:
В уравнении (2.22) для N принимают знак «минус» при внецентренном сжатии, знак «плюс» – при внецентренном растяжении; N = 0 при изгибе. Высоту сжатой зоны х для сечений, работающих по случаю 2, когда разрушение происходит по сжатому бетону хрупко, а напряжения в арматуре As не достигают расчетного сопротивления арматуры растяжению Rs,определяют также из уравнения (2.22), заменяя в нем Rs напряжением σs < Rs. Напряжения в продольной арматуре Аs, расположенной у растянутой или менее сжатой грани, могут изменяться в широком диапазоне, от предельных напряжений сжатия Rsc до напряжений растяжения Rs. Их величина зависит от высоты сжатой зоны бетона х. Чтобы представить эту зависимость, рассмотрим схему деформирования нормального сечения в виде плоского поворота сечения (рис. 36). Из этой схемы имеем зависимость:
При разрушении бетона в сжатой зоне краевые деформации в бетоне соответствуют некоторым предельным значениям
Рис. 36. Схема распределения деформаций и напряжений в поперечном сечении элемента: а – сечение элемента и участок элемента с трещиной; б – эпюра деформаций; в – эпюра напряжений; г, д – диаграммы σ – ε для бетона и арматуры
Для мягких сталей, имеющих физический предел текучести, при увеличении деформаций растяжения арматуры выше значений, соответствующих началу текучести, напряжения в арматуре остаются постоянными и равными её пределу текучести или Rs. В этом случае напряжения должны быть ограничены σs ≤ Rs. Граничная относительная высота сжатой зоны бетона
где es,el – относительная деформация растянутой арматуры при напряжениях, равных Rs:
eb,ult – относительная деформация сжатого бетона при напряжениях, равных Rb, принимаемая равной 0,0035.
ЛИТЕРАТУРА
1. СНиП 2.01.07-85*. Нагрузки и воздействия [Текст]: утв. Госстроем России 29.05.2003. – М.: ГУП ЦПП, 2003. – 44 с. 2. СНиП 52-01-2003. Бетонные и железобетонные конструкции. Основные положения [Текст]: утв. Государственным комитетом Российской Федерации по строительству и жилищно-коммунальному комплексу от 30.06.2003: взамен СНиП 2.03.01-84: дата введ. 01.03.2004. – М.: ГУП НИИЖБ, 2004. – 26 с. 3. СП 52-101-2003. Бетонные и железобетонные конструкции без предварительного напряжения арматуры [Текст]: утв. Государственным комитетом Российской Федерации по строительству и жилищно-коммунальному комплексу от 30.06.2003: взамен СНиП 2.03.01-84: дата введ. 01.03.2004. – М.: ГУП НИИЖБ, 2004. – 55 с. 4. Евстифеев, В.Г. Железобетонные конструкции (расчет и конструирование) [Текст]: учебное пособие для студентов специальности ПГС / – СПб.: Иван Федоров, 2005. – 192 с.: ил. 5. Байков, В. Н. Железобетонные конструкции. Общий курс [Текст]: учеб. для вузов /В.Н. Байков, Э.Е. Сигалов. Изд. 5-е, перераб. и доп. – М.: Стройиздат, 1991. – 767 с.: ил. 6. Бондаренко, В.М. Железобетонные и каменные конструкции. [Текст]: учеб. для строит. спец. вузов /В.М. Бондаренко, Р.О. Бакиров, В.Г. Назаренко, В.И. Римшин; Под ред. В. М. Бондаренко. Изд. 3, исправл. – М.: Высш. шк., 2004. – 876 с.: ил.
Содержание ВВЕДЕНИЕ. 3 1. ОСНОВНЫЕ ФИЗИКО-МЕХАНИЧЕСКИЕ СВОЙСТВА БЕТОНА, СТАЛЬНОЙ АРМАТУРЫ И ЖЕЛЕЗОБЕТОНА.. 14 1.1. Бетон. 14 1.1.1. Общие сведения. 14 1.1.2. Структура (строение) бетона. 15 1.1.3. Усадка бетона и начальные напряжения. 16 1.1.4. Прочность бетона. 18 1.1.5. Классы и марки бетона. 24 1.1.6. Деформативность бетона. 28 1.1.7. Модуль деформаций бетона. 37 1.2. Арматура для железобетонных конструкций. 38 1.2.1. Назначение арматуры и требования к ней. 38 1.2.2. Виды арматуры.. 39 1.2.3. Физико-механические свойства арматурных сталей. 39 1.2.4. Классификация арматуры по основным характеристикам. Сортамент арматуры 42 1.2.5. Сварные арматурные изделия. 45 1.2.6. Соединения арматуры.. 48 1.3. Железобетон. 53 1.3.1. Общие сведения. 53 1.3.2. Содержание арматуры.. 53 1.3.3. Значение трещиностойкости. 53 1.3.4. Сцепление арматуры с бетоном. 55 1.3.5. Анкеровка арматуры в бетоне. 58 1.3.6. Усадка бетона при наличии арматуры.. 61 1.3.7. Ползучесть бетона при наличии арматуры.. 64 1.3.8. Коррозия железобетона и меры защиты от неё. 66 1.3.9. Защитный слой бетона и минимальные расстояния между стержнями. 68 2. ЭКСПЕРИМЕНТАЛЬНЫЕ ОСНОВЫ ТЕОРИИ СОПРОТИВЛЕНИЯ ЖЕЛЕЗОБЕТОНА И МЕТОДЫ РАСЧЕТА ЖЕЛЕЗОБЕТОННЫХ КОНСТРУКЦИЙ 69 2.1. Общие сведения. 69 2.2. Три стадии напряжённо-деформированного состояния железобетонных элементов 69 2.3. Методы расчёта железобетонных конструкций. 73 2.4. Метод расчёта железобетонных конструкций по предельным состояниям. 73 2.4.1. Сущность метода. 73 2.4.2. Две группы предельных состояний. 74 2.4.3. Расчётные факторы.. 74 2.4.4. Классификация нагрузок. Нормативные и расчётные нагрузки. 75 2.4.5. Степень ответственности зданий и сооружений. 76 2.4.6. Нормативные и расчётные сопротивления бетона. 77 2.4.7. Нормативные и расчётные сопротивления арматуры.. 79 2.4.8. Структура расчётных формул. 80 2.4.9. Общий способ расчёта прочности железобетонных элементов. 83 ЛИТЕРАТУРА.. 87
|
||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 656; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.009 с.) |

 (сумма моментов всех сил относительно оси, проходящей через центр тяжести арматуры Аs,равна нулю); для случая изгиба оно выглядит так (рис. 35, а):
(сумма моментов всех сил относительно оси, проходящей через центр тяжести арматуры Аs,равна нулю); для случая изгиба оно выглядит так (рис. 35, а): (2.20)
(2.20) (2.21)
(2.21) (2.22)
(2.22) отсюда
отсюда  или
или  (2.23)
(2.23) , которые можно принять за постоянную величину. Отсюда видно, что деформации в арматуре
, которые можно принять за постоянную величину. Отсюда видно, что деформации в арматуре 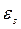 , а следовательно, и напряжения в ней σs, которые определяются по диаграмме σs –
, а следовательно, и напряжения в ней σs, которые определяются по диаграмме σs –  , являются функцией от ξ. Связь между деформациями арматуры и высотой сжатой зоны имеет гиперболический характер. Чем меньше высота сжатой зоны, тем выше напряжения в продольной арматуре и наоборот. Эту закономерность можно увидеть непосредственно из схемы деформирования нормального сечения (рис. 36).
, являются функцией от ξ. Связь между деформациями арматуры и высотой сжатой зоны имеет гиперболический характер. Чем меньше высота сжатой зоны, тем выше напряжения в продольной арматуре и наоборот. Эту закономерность можно увидеть непосредственно из схемы деформирования нормального сечения (рис. 36).
 , при которой напряжения в арматуре As ещё достигают Rs,может быть найдена из формулы (2.24):
, при которой напряжения в арматуре As ещё достигают Rs,может быть найдена из формулы (2.24): (2.24)
(2.24) (2.25)
(2.25)


