
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Метод последовательной смены стационарных состоянийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Данный метод предложен И.А.Чарным и основан на предположении, что давление в пласте изменяется во времени значительно медленнее, чем по координате. Поэтому производную по времени можно в первом приближении отбросить, в результате чего для давления получается уравнения Лапласа, описывающее стационарный процесс.
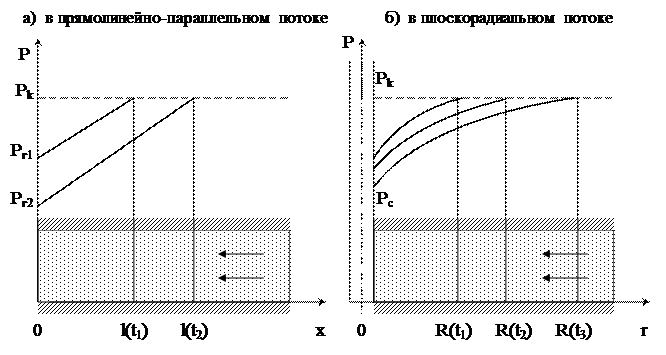
Рис. 6.1. Кривые распределения давления по методу ПССС В каждый момент времени вся область движения жидкости условно разделяется на две области: возмущенную и невозмущенную. При этом предполагается, что в возмущенной области, начинающейся от стенки скважины, давление распределяется так, как будто бы движение жидкости в ней установившееся. Внешняя граница этой области служит в данный момент контуром питания. В невозмущенной области пласта давление всюду постоянно и равно начальному. Закон движения подвижной границы раздела двух областей определяется при помощи уравнения материального баланса и граничных условий.
Метод А.М.Пирвердяна Неустановившийся прямолинейно-параллельный фильтрационный поток, так же как и в предыдущем случае, разбивается на две области – возмущенную и невозмущенную. Однако в отличие от метода ПССС распределение давления в возмущенной области задается в виде квадратичной параболы, касательная к которой в точке
Рассмотрим два случая применительно к прямолинейно-параллельному потоку.
Метод интегральных соотношений Метод предложен Г.И.Баренблаттом и основан на следующих предпосылках: а) в каждый момент времени пласт делится на конечную возмущенную область и невозмущенную область, в которой движение отсутствует; б) в возмущенной области распределение давления представляется в виде многочлена с коэффициентами, зависящими от времени; Для прямолинейно-параллельного потока:
Для плоскорадиального потока:
Число членов n выбирается в зависимости от желаемой точности решения; в) коэффициенты a0, a1,…,an, а также размер области возмущения l(t) или R(t) находятся из условий на галерее (забое скважины), из условий непрерывности и гладкости кривой давления на границе области возмущения, а также из особых интегральных соотношений. Если принять в формуле (6.20) n=1, а в формуле (6.21) n=0, то получатся решения, соответствующие методу ПССС. Если n=2, то из метода интегральных соотношений вытекает как частный случай метод А.М.Пирвердяна. Рассмотрим задачу плоскорадиальной неустановившейся фильтрации упругой жидкости к скважине радиусом Rc, пущенной в эксплуатацию в момент времени t=0 с постоянным дебитом Q. В начальный момент времени давление в пласте постоянно и равно Рк. Распределение давления в возмущенной области пласта
Коэффициенты a0, a1 и a2 определяются из условий на забой скважины и на границе возмущенной области. Условие на забое:
На границе возмущенной области имеем:
Тогда:
При этом слагаемые, пропорциональные Rc или Rc2, отброшены вследствие их малости. После подстановки в формулу распределения давления будем иметь:
Закон движения границы возмущенной области:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 825; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.23.101.241 (0.007 с.) |

 ,
0 £ x £ l(t)
,
0 £ x £ l(t)


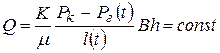


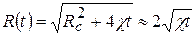
 при
при  ;
;
 при
при 
 при
при  ;
;
 при
при 


 где
где  - безразмерный радиус во-ронки депрессии, R(t)/Rc; t - безраз-мерное время
- безразмерный радиус во-ронки депрессии, R(t)/Rc; t - безраз-мерное время
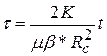
 при
при  горизонтальна. Это обеспечивает плавное смыкание профиля давлений в возмущенной и невозмущенной областях.
горизонтальна. Это обеспечивает плавное смыкание профиля давлений в возмущенной и невозмущенной областях.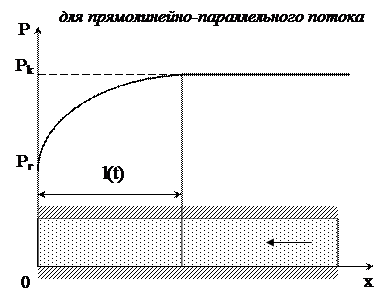




 при
при  ;
;

 при
при 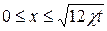 ;
;
 при
при 

 ; (6.20)
; (6.20)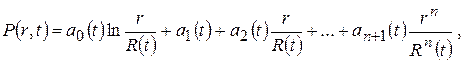
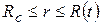 . (6.21)
. (6.21)
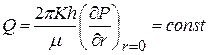 при
при 
 при
при 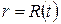 ,
,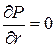 при
при 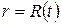 - условие гладкости кривой давления.
- условие гладкости кривой давления. ;
; 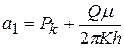 ;
; 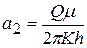 .
.
 .
.


