
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрия червячной передачи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Виды червячных передач. Качество и работоспособность червячной передачи зависят от формы, твердости, шероховатости и точности изготовления винтовой поверхности витка червяка. Различают линейчатые и нелинейчатые червяки в зависимости от того, могут или не могут винтовые поверхности витков червяка быть образованы прямой линией. Нарезание линейчатых винтовых поверхностей осуществляют на универсальных токарно-винторезных станках, когда прямолинейная кромка резца воспроизводит эвольвентную, конволютную или архимедову поверхность. Нелинейчатую винтовую поверхность получают дисковыми фрезами конусной или тороидальной формы. В соответствии с этим червячные передачи бывают с эвольвентными, архимедовыми, конволютными и нелинейчатыми червяками. Получение того или иного вида винтовой поверхности у витков червяка зависит от способа нарезания.
Рисунок 49 – Геометрия эвольвентного червяка Эвольвентный червяк получают при установке прямолинейной кромки резца в плоскости, касательной к основному цилиндру с диаметром d С целью получения высокой поверхностной твердости витков и повышения тем самым качественных показателей передачи применяют термическую обработку с последующим шлифованием рабочих поверхностей витков. Эвольвентные червяки могут быть с высокой точностью прошлифованы плоской поверхностью шлифовального круга. Производительные способы нарезания и простота шлифования обусловливают высокую технологичность эвольвентных червяков. Архимедов червяк получают при расположении режущих кромок резца в плоскости, проходящей через ось червяка. Архимедовы червяки имеют в осевом сечении прямолинейный профиль с углом 2α, равным профильному углу резца (рис. 50,а). В торцовом сечении профиль витка очерчен архимедовой спиралью. Боковые поверхности витков архимедовых червяков могут быть прошлифованы только специально профилированным по сложной кривой шлифовальным кругом. Поэтому упрочняющую термообработку и последующее шлифование не выполняют и применяют архимедовы червяки с низкой твердостью в тихоходных передачах с невысокими требованиями к нагрузочной способности и ресурсу.
Рисунок 50 – Архимедов червяк (а) и конволютный червяк (б) Конволютный червяк получают при установке режущих кромок резца в плоскости, касательной к цилиндру с диаметром dx (0< dx<db) и нормальной к оси симметрии впадины. В этой плоскости червяки имеют прямолинейный профиль впадины (рис. 50,б). Конволютные червяки имеют в осевом сечении выпуклый профиль, в торцовом сечении профиль витка очерчен удлиненной эвольвентой. Недостатком передач с конволютными червяками является сложная форма инструмента для шлифования червяков и невозможность получения точных фрез для нарезания зубьев червячных колес. Передачи с конволютными червяками так же, как и с архимедовыми, имеют ограниченное применение, в основном в условиях мелкосерийного производства. Нелинейчатые червяки нарезают дисковыми фрезами конусной или тороидальной формы. Витки таких червяков во всех сечениях имеют криволинейный профиль: в сечении, нормальном к оси симметрии впадины, выпуклый (рис. 51,а), в осевом сечении – вогнутый (рис. 51,б). Рабочие поверхности витков нелинейчатых червяков с высокой точностью шлифуют конусным или тороидным кругом. Передачи с нелинейчатыми червяками характеризует повышенная нагрузочная способность, их считают перспективными.
Рисунок 51 – Нелинейчатые червяки Для силовых передач следует применять эвольвентные и нели нейчатые червяки. Геометрические размеры червяка и колеса определяют по формулам, аналогичным формулам для зубчатых колес. В червячной передаче расчетным является осевой модуль червяка т, равный торцовому модулю червячного колеса. Значения т, мм, выбирают из ряда:...4; 5; 6,3; 8.... Основными геометрическими размерами червяка являются (рис. 49): · делительный диаметр, т.е. диаметр такого цилиндра червяка, на котором толщина витка равна ширине впадины:
где q – число модулей в делительном диаметре червяка или коэффициент диаметра червяка. С целью сокращения номенклатуры зуборезного инструмента значения q стандартизованы: 8; 10; 12,5; 16; 20; · расчетный шаг червяка:
· ход витка:
где z · угол α профиля: для эвольвентных, архимедовых и конволютных червяков а = 20°; для червяков, образованных тором, α = 22°; · диаметр вершин витков:
· диаметр впадин витков:
· делительный угол подъема линии витка (см. рис. 52):
· длина нарезанной части –b Для червяка в передаче со смещением дополнительно вычисляют: · диаметр начального цилиндра (начальный диаметр):
· угол подъема линии витка на начальном цилиндре:
где х – коэффициент смещения.
Рисунок 52 – Определение угла подъема винтовой линии Геометрические размеры венца червячного колеса. Зубья на червячном колесе чаще всего нарезают червячной фрезой, которая представляет собой копию червяка, с которым будет зацепляться червячное колесо. Только фреза имеет режущие кромки и несколько больший (на двойной размер радиального зазора в зацеплении) наружный диаметр. Основные геометрические размеры венца червячного колеса определяют в среднем его сечении. Делительный d2 и совпадающий с ним начальный dwi диаметр колеса при числе z 2 зубьев (рис. 53):
Рисунок 53 – Геометрия червячного колеса Межосевое расстояние червячной передачи:
Червячные передачи со смещением выполняют в целях обеспечения стандартного или заданного значения межосевого расстояния. Осуществляют это, как и в зубчатых передачах, смещением на (хт) фрезы относительно заготовки при нарезании зубьев колеса (рис. 53):
Для стандартных редукторов aw:...80, 100, 125, 140, 160,.... Для нарезания зубьев колес в передачах со смещением и без смещения используют один и тот же инструмент. Поэтому нарезание со смещением выполняют только у колеса. При заданном межосевом расстоянии коэффициент смещения инструмента. Значения коэффициента х смещения инструмента выбирают по условию неподрезания и незаострения зубьев. Предпочтительны положительные смещения, при которых одновременно повышается прочность зубьев колеса. Рекомендуют для передач с червяком: – эвольвентным 0 ≤ х ≤ 1 (предпочтительно х = 0,5); – образованным тором 1,0 ≤ х ≤ 1,4 (предпочтительно x:= 1,1–1,2). Диаметр вершин зубьев (рис. 53):
Диаметр впадин зубьев:
Наибольший диаметр червячного колеса:
где k = 2 для передач с эвольвентным червяком; k = 4 для передач, нелинейчатую поверхность которых образуют тором. Ширина
Червячное колесо является косозубым с углом у w наклона зуба. Условный угол 2δ обхвата для расчета на прочность находят по точкам пересечения окружности диаметром (dal – 0,5т) с линиями торцов венца червячного колеса. Кинематика передачи. Передаточное число и червячной передачи определяют по условию, что за каждый оборот червяка колесо поворачивается на угол, охватывающий число зубьев колеса, равное числу витков червяка. Полный оборот колесо совершает за z2 и
где d γ 1 – делительный угол подъема линии витка;
Во избежание подреза основания ножки зуба в процессе нарезания зубьев принимают z2 ≥ 26. Оптимальным является z2 =32...63. Для червячных передач стандартных редукторов передаточные числа выбирают из ряда:...31,5; 40; 50; 63; 80 Точность червячных передач. Для червячных передач установлены 12 степеней точности, для каждой из которых предусмотрены нормы кинематической точности, нормы плавности и нормы контакта зубьев и витков. В силовых передачах наибольшее применение имеют 7–я (vCK ≤ 10 м/с), 8–я (vCK ≤ 5 м/с) и 9–я (vCK ≤ 2 м/с) степени точности. КПД червячной передачи. Роль смазывания в червячной передаче еще важнее, чем в зубчатой, так как в зацеплении происходит скольжение витков червяка вдоль контактных линий зубьев червячного колеса. КПД червячного зацепления определяют по формуле:
где γ w – угол подъема винтовой линии; φ' – приведенный угол трения; f'= tgφ' – приведенный коэффициент трения (коэффициент трения, найденный с учетом угла а профиля витка). Значения угла φ' трения в зависимости от скорости скольжения получают экспериментально для червячных передач на опорах с подшипниками качения, т.е. в этих значениях учтены потери мощности в подшипниках качения, в зубчатом зацеплении и на размешивание и разбрызгивание масла. Величина φ' снижается при увеличении vCK, так как при больших скоростях скольжения в зоне контакта создаются благоприятные условия для образования масляного слоя, разделяющего витки червяка и зубья колеса и уменьшающего потери в зацеплении. Численное значение Обычно в червячных передачах γw ≤ 27°. Большие углы подъема выполнимы в передачах с четырех–заходным червяком и с малыми передаточными числами.
Рисунок 57 – График зависимости КПД Червячные передачи имеют сравнительно низкий КПД, что ограничивает область их применения ( Силы в зацеплении. Силу взаимодействия червяка и колеса принимают сосредоточенной и приложенной в полюсе зацепления по нормали к рабочей поверхности витка. Ее задают тремя взаимно перпендикулярными составляющими: Ft Fa, Fr. Для наглядности изображения сил червяк и червячное колесо на рис. 58, а условно выведены из зацепления. Окружная сила Ft2 на червячном колесе:
где Т2 – вращающий момент на червячном колесе, Н·м; d2 – делительный диаметр колеса, мм. Осевая сила Fal на червяке численно равна Ft2:
Окружная сила Ft1 на червяке:
где
Осевая сила Fa2 на червячном колесе численно равна Ft1:
Радиальная сила Fr1 на червяке (радиальная сила Fr2 на колесе численно равна Fr1), рис. 58,б:
Направление силы Ft2 всегда совпадает с направлением вращения колеса, а сила Ftl направлена в сторону, противоположную вращению червяка.
Рисунок 58 – Силы, действующие в червячном зацеплении
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 3064; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.175.191 (0.007 с.) |


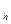 (рис. 49). Левую и правую стороны витка нарезают соответственно резцами 1 и 2 (см. также сечения В–В и Б–Б). В торцовом сечении (сечении, перпендикулярном оси червяка) профиль витка червяка очерчен эвольвентой, в осевом сечении (А–А) – криволинейный (выпуклый). Эвольвентный червяк представляет собой цилиндрическое косозубое колесо эвольвентного профиля с числом зубьев, равным числу витков червяка, и с большим углом наклона зубьев.
(рис. 49). Левую и правую стороны витка нарезают соответственно резцами 1 и 2 (см. также сечения В–В и Б–Б). В торцовом сечении (сечении, перпендикулярном оси червяка) профиль витка червяка очерчен эвольвентой, в осевом сечении (А–А) – криволинейный (выпуклый). Эвольвентный червяк представляет собой цилиндрическое косозубое колесо эвольвентного профиля с числом зубьев, равным числу витков червяка, и с большим углом наклона зубьев.

 , (86)
, (86) , (87)
, (87) , (88)
, (88) – число витков червяка: 1, 2 или 4 (z
– число витков червяка: 1, 2 или 4 (z  , (89)
, (89) , (90)
, (90) , (91)
, (91) , (92)
, (92)
 , (93)
, (93)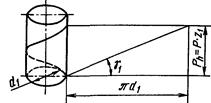
 , (94)
, (94)
 , (95)
, (95) , (96)
, (96) , (97)
, (97) , (98)
, (98) , (99)
, (99) венца червячного колеса зависит от числа витков червяка:
венца червячного колеса зависит от числа витков червяка: при z
при z  при z =4, (100)
при z =4, (100)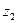 оборотов червяка:
оборотов червяка: , (101)
, (101) , п2 – частоты вращения червяка и колеса;
, п2 – частоты вращения червяка и колеса; и z2 – число витков червяка и число зубьев колеса.
и z2 – число витков червяка и число зубьев колеса.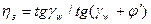 , (102)
, (102)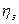 увеличивается с ростом угла γ w подъема на начальном цилиндре до γ w
увеличивается с ростом угла γ w подъема на начальном цилиндре до γ w  40° (рис. 57).
40° (рис. 57).
 от угла γ w
от угла γ w , (103)
, (103) , (104)
, (104) , (105)
, (105)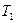 – вращающий момент на червяке, Н·м;
– вращающий момент на червяке, Н·м; – КПД, dw1 – в мм.
– КПД, dw1 – в мм. , (106)
, (106) , (107)
, (107)



