
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема о связи функции, её предела и бесконечно малой функции.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема о связи функции, её предела и бесконечно малой функции. Если функция ƒ(х) имеем предел, равный b, то ее можно представить как сумму числа b и бесконечно малой функции α(х), т.е. Док-во: Пусть
Бесконечно большие и бесконечно малые функции, их свойства. Бесконечно малая функция: Последовательность Например, последовательность чисел Последовательность Функция называется бесконечно большой в окрестности точки х 0, если
Свойства: 1) Сумма конечного числа бесконечно малых — бесконечно малая. 2) Произведение бесконечно малых — бесконечно малая. 3) Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая. 4) Если
Сравнение бесконечно малых функций, эквивалентные бесконечно малые функции, их свойства. Общим у всех бесконечно малых функций явл. их стремление к нулю, однако «скорость» стремления к нулю может быть различной. Пусть α(х) и β(х)- бесконечно малые, при х→х0 функции, если Бесконечно малые функцииα(x) иβ(x) называются эквивалентными при x Т1) Предел отношения двух бесконечно малых функций равен пределу отношения функций, им эквивалентных, Т2) Сумма нескольких бесконечно малых функций различных порядков малости эквивалентна слагаемому низшего порядка малости.
Первый и второй замечательный предел функции. Первый и второй замечательный предел используют для раскрытия неопределенностей, содержащих тригонометрические функции Первый замечательный предел. Второй замечательный предел. Док-во первого: Рассм. Окружность единичного радиуса и < х? (0;
1< Значит (перейдём к обратным): 1< Если х? (- 1 > Таким образом неравенство справедливы для любого х? (- Док-во второго: Сделав во втором замечательном пределе замену
Непрерывность функций. Точки разрыва функции, их классификация. Функция у=f(x) называется непрерывной в точке Точка х0 наз. точкой разрыва функции f(x), если в этой точке нарушается условие непрерывности, т.е. либо Точки разрыва можно разбить на 2 класса: а)1-го рода, для которых б) 2-го рода, для которых хотя бы один из пределов Точки разрыва 1-го рода наз. также точками устранимого разрыва или конечного скачка, а 2-го рода точками бесконечного разрыва. Если Среди точек разрыва 1-го рода выделяют точки устранимого разрыва – точки для которых f(x0)=
Связь между непрерывностью и дифференцируемостью функции. Если функция дифференцируема в точке, то она в этой точке непрерывна. Пример: y =
-x1x ≤ 0;
Этот пример показывает, что из непрерывности функции в точке, не следует её дифференцируемость. Асимптоты графика функции. Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат. Различают вертикальные и наклонные асимптоты. Прямая X=a является вертикальной асимптотой графики функции y=f(x), если, по крайней мере, один из односторонних пределов в точке x=a равен бесконечности т.е.
Прямая y=k1x+b1 является наклонной асимптотой при x->+∞ если существуют оба предела
Аналогично, если существуют пределы K1= То прямая y=k2x+b2 является наклонной асимптотой приx->-∞ Если k=0 и существует Если вертикальных асимптот может быть любое число, то наклонных асимптот не может быть более 2-ух. Теорема о связи функции, её предела и бесконечно малой функции. Если функция ƒ(х) имеем предел, равный b, то ее можно представить как сумму числа b и бесконечно малой функции α(х), т.е. Док-во: Пусть
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 8830; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.140.198.3 (0.011 с.) |

 , то ƒ(х)=b+α(х), где α(х)- бесконечно малая величина.
, то ƒ(х)=b+α(х), где α(х)- бесконечно малая величина. тогда
тогда 
 , значит
, значит  ,
,  – бесконечно малая величина.
– бесконечно малая величина. называется бесконечно малой, если
называется бесконечно малой, если  .
. — бесконечно малая. Функция называется бесконечно малой в окрестности точки x0, если
— бесконечно малая. Функция называется бесконечно малой в окрестности точки x0, если  . Функция называется бесконечно малой на бесконечности, если
. Функция называется бесконечно малой на бесконечности, если  либо
либо  . Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если
. Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то
, то  ,
,  .
. .
. . Функция называется бесконечно большой на бесконечности, если
. Функция называется бесконечно большой на бесконечности, если  либо
либо  .
. — бесконечно большая последовательность.
— бесконечно большая последовательность. , то говорят, что α(х) и β(х)- одного порядка малости. Если же
, то говорят, что α(х) и β(х)- одного порядка малости. Если же  , то говорят, что α(х)-бесконечно малая более высокого порядка малости, чем β(х) и пишут α(х)=0(β(х)).
, то говорят, что α(х)-бесконечно малая более высокого порядка малости, чем β(х) и пишут α(х)=0(β(х)). a, если
a, если  . Если α(х) – бесконечно малая функция, то справедливы основные эквивалентности: sinα(x)~α(x); tgα(x)~α(x);arcsinα(x)~ α(x); arctgα(x)~α(x); eα(x)
. Если α(х) – бесконечно малая функция, то справедливы основные эквивалентности: sinα(x)~α(x); tgα(x)~α(x);arcsinα(x)~ α(x); arctgα(x)~α(x); eα(x)  ~α(x); ln(1+α(x))~α(x); aα(x)
~α(x); ln(1+α(x))~α(x); aα(x)  . При вычислении пределов используются следующие теоремы об эквивалентных бесконечно малых функциях:
. При вычислении пределов используются следующие теоремы об эквивалентных бесконечно малых функциях:

 )
)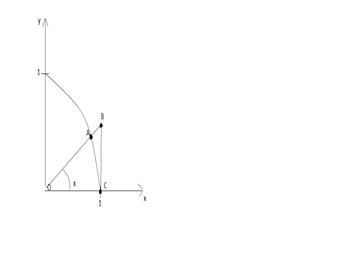 Из рис. следует, что:
Из рис. следует, что:



 >
> 
 , то – х? (0;
, то – х? (0;  , тогда:
, тогда:
 отличного от нуля. Т.к.
отличного от нуля. Т.к.  ,
,  , то
, то 
 = t, получим
= t, получим  = е.
= е. , если она определена некоторой окрестностью этой точки и предел
, если она определена некоторой окрестностью этой точки и предел  . C геометрической точки зрения непрерывность функции означает, что график функции не имеет «разрывов».
. C геометрической точки зрения непрерывность функции означает, что график функции не имеет «разрывов». , либо
, либо 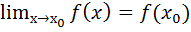 .
. и
и  существуют, но не равны f(x0);
существуют, но не равны f(x0); конечны, но не равны, то их разность
конечны, но не равны, то их разность 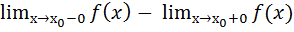 – наз. скачком функции.
– наз. скачком функции. =
=  но они ≠ f(x0). Этот разрыв можно устранить, доопределив функцию
но они ≠ f(x0). Этот разрыв можно устранить, доопределив функцию =
= 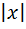
 y= x1x > 0
y= x1x > 0
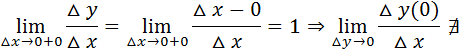
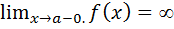 или
или 
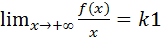 и b1=
и b1= 
 и b1=
и b1= 
 , то получаем горизонтальную асимптоту y=b как частный случай наклонной.
, то получаем горизонтальную асимптоту y=b как частный случай наклонной.


