
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Условия возрастания и убывания функций. Экстремумы.Содержание книги
Поиск на нашем сайте
Функция называется возрастающей (убывающей) в некотором промежутке, если в этом промежутке каждому большему значению аргумента соответствует большее (меньшее) значение функции. возрастающие, как и убывающие функции, называются монотонными. Возрастание и убывание функции y = f{x) определяется знаком ее производной: если в некотором интервале f'(x) > 0, то функция возрастает, а если f'(x) < 0, то функция убывает в этом интервале. Первое правило нахождения экстремумов функции f(x) (по первой производной): · Находим область определения функции D(f)• · Ищем первую производную функции f '(x). · Находим критические точки первой производной. · Определяем знак производной f '(x). слева и справа от критической точки, в которой функция непрерывна. Если знак изменяется с плюса на минус, то в данной точке функция имеет максимум, если с минуса на плюс, то - минимум. Если же знак производной не изменяется, то в данной точке экстремума нет.
Второе правило нахождения точек экстремума (по второй производной): · Находим область определения функции D(f). · Ищем первую производную функции f '(x) · Находим точки, в которых f '(x) = 0, а функция f(х) непрерывна. · Ищем вторую производную f "(x) · Во вторую производную f "(x) подставляем каждое из значений, полученных в п. 3. Если f "(хо)>0; то в точке х0 функция имеет минимум, если f "(хо)<0, то - максимум. Если f ”(хо) = 0, то вопрос о наличии экстремума остается открытым (можно воспользоваться первым правилом).
Выпуклость. Точки перегиба. Достаточное условие существования точек перегиба Кривая называется выпуклой (вогнутой) в некотором промежутке, если она расположена ниже (выше) касательной, проведенной к кривой в любой точке этого промежутка. Выпуклость или вогнутость кривой, являющейся графиком функции у = f(x).Характеризуется знаком второй производной f“(x) > 0, а именно: если в некотором промежутке f “(х)>О, то кривая вогнута, если f “(х)<0, то кривая выпуклая в этом промежутке. Следовательно, нахождение промежутков выпуклости и вогнутости сводится к нахождению промежутков знакопостоянства ее второй производной f ‘’(х). Точкой перегиба кривой называется такая ее точка, которая отделяет участок выпуклости от участка вогнутости. Точками перегиба графика функции y = f(х) могут быть только точки, в которых вторая производная изменяет свой знак, т.е. точки, находящиеся внутри области определения функции f(x)в которых вторая производнаяf ‘’(х) обращается в нуль или терпит разрыв. Такие точки называются критическими точками второй производной. Точками перегиба графика функции у= f(х) будут лишь те критические точки второй производной, при переходе через которые f ‘’(x) меняет знак. Отсюда получаем правило нахождения промежутков выпуклости и вогнутости и точек перегиба графика функции: 1) Находим область определении функцииD(f). 2) Ищем 2-ую производную функцииf f (x). 3) Определяем точки, в которых вторая производная f ‘’(x) обращается в нуль или терпит разрыв (критические точки 2-ой производной)| 4) Находим промежутки, на которые разбивают области определенияD(f) критические точки. 5) Определяем знак f ‘’(x) на каждом из полученных промежутков: если f‘’(x)> о, то это промежуток вогнутости; если же f’’(x)< О, то это промежуток выпуклости. 6) Те из граничных точек промежутков, в которых функции f(x) непрерывна, а вторая производная f’’(x) изменяет свой знак при переходе через них, являются точками перегиба: При нахождении интервалов выпуклости и вогнутости и точек перегиба удобно результаты исследования записывать и таблицу изменения знаков второй производной. Асимптоты графика функции. Асимптотой кривой называется прямая, к которой неограниченно приближается точка кривой при неограниченном удалении её от начала координат. Различают вертикальные и наклонные асимптоты. Прямая X=a является вертикальной асимптотой графики функции y=f(x), если, по крайней мере, один из односторонних пределов в точке x=a равен бесконечности т.е.
Прямая y=k1x+b1 является наклонной асимптотой при x->+∞ если существуют оба предела
Аналогично, если существуют пределы K1= То прямая y=k2x+b2 является наклонной асимптотой приx->-∞ Если k=0 и существует Если вертикальных асимптот может быть любое число, то наклонных асимптот не может быть более 2-ух.
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 803; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.215.186 (0.008 с.) |

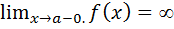 или
или 
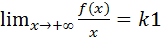 и b1=
и b1= 
 и b1=
и b1= 
 , то получаем горизонтальную асимптоту y=b как частный случай наклонной.
, то получаем горизонтальную асимптоту y=b как частный случай наклонной.


