
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основные логические операцииСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Таблица 3.1
Приоритет связок соответствует номеру в таблице 3.1:
Таблица истинности для основных бинарных логических операций Таблица 3.2
Истинность или ложность получаемых таким образом высказываний зависит от истинности и ложности исходных высказываний и соответствующей трактовки связок как операций над высказываниями. В алгебре логики логические операции чаще всего описываются при помощи таблиц истинности. Формулы алгебры логики Переменная, значениями которой являются высказывания, называется пропозициональной переменной. Правила сокращения записей в пропозициональных формулах:
3. Примеры выполнения задания к практическому занятию №3 Решение логических задач средствами алгебры логики Пример 6. Составить таблицу истинности для данной формулы: P= ((x Þz) | ((x Ù y) Û (y Ù z)))¯(ØyÚØx) Решение.
В таблице истинности 3.3 приводится решение примера 6. Таблица 3.3
Примечание 1. Каждую операцию следует включить в таблицу истинности вида 3.3. 2. Нельзя в одном столбце выполнять более одной операции. 3. При выполнении задания следует учесть последовательность выполнения действий с учётом их приоритета, согласно которому в первую очередь выполняются операции в скобках. Из логических операций вначале выполняется отрицание, затем конъюнкция и т.д., как указано в таблице 3.1. В таблице 3.3 последовательность выполнения действий отражается в третьей строке номером логической операции с учётом приоритета. 4. Формула в задании может быть записана с учётом сокращений в виде: ((x ® z) | ((x × y) ~ (y × z)))¯(Øy + Øx). Задания к практическому занятию № 3
Таблица 3.4
Задание ИДЗ №3 по теме «Алгебра логики» в Приложении №1 (Задание 3). Вопросы для самоконтроля к практическому занятию № 3. Тема «Алгебра логики» 1. Логическая операция АÙВ – это: 1) импликация; 2) конъюнкция; 3) дизъюнкция 4) эквиваленция. 2. Логическая операция АÚВ – это: 1) импликация; 2) конъюнкция; 3) дизъюнкция 4) эквиваленция. 3. Логическая операция АÞВ – это: 1) импликация; 2) конъюнкция; 3) дизъюнкция 4) эквиваленция. 4. Логическая операция АÛВ – это 1) импликация; 2) конъюнкция; 3) дизъюнкция 4) эквиваленция. 5. С помощью таблицы истинности получается результат логической функции F=А Þ B Выбрать строку, которая соответствует результату логической функции в таблице.
1) 0 1 1 1; 2) 0 0 0 1; 3) 0 1 1 0; 4) 1 1 0 1. 6. Пусть через А обозначим высказывание «студент знает математику», через В обозначим высказывание «студент любит спорт». Выбрать конъюнкцию, дизъюнкцию, импликацию, эквиваленцию этих высказываний. 1) «Если студент знает математику, то студент любит спорт»; 2) «студент знает математику или студент любит спорт»; 3) «студент знает математику и студент любит спорт»; 4) «студент знает математику тогда и только тогда, когда студент любит спорт». 7. Логическая операция эквиваленция обозначается знаком: 1) Ú; 2) Ù; 3) Û; 4) Þ. 8. Выбрать логическую операцию F= А?В, которая соответствует таблице истинности.
1) конъюнкция; 2) эквиваленция; 3) дизъюнкции; 4) импликация. 9. Пусть через А обозначим высказывание «Ада Лавлейс-первый в мире программист», через В обозначим высказывание «Джон фон Нейман - автор классического компьютера». Выбрать конъюнкцию, дизъюнкцию, импликацию, эквиваленцию этих высказываний. 1) «Если Ада Лавлейс-первый в мире программист, то Джон фон Нейман автор классического компьютера»; 2) «Ада Лавлейс-первый в мире программист или Джон фон Нейман автор классического компьютера»; 3) «Ада Лавлейс-первый в мире программист в мире и Джон фон Нейман автор классического компьютера»; 4) «Ада Лавлейс-первый в мире программист в мире тогда и только тогда, когда Джон фон Нейман автор классического компьютера».
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1158; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.26.184 (0.009 с.) |

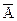
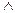 умножение
умножение
 сложение
сложение

 ; (~)
; (~)
 (стрелка Пирса)
(стрелка Пирса)
 B
B

 ;
;


