Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Заряд белковой молекулы. Изоэлектрическая точка белка.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Белки имеют в своём составе радикалы лизина, аргинина, гистидина, глутаминовой и аспарагиновой кислот, содержащие функциональные группы, способные к ионизации (ионогенные группы). Кроме того, на N- и С-концах полипептидных цепей имеются α-амино- и α-карбоксильная группы, также способные к ионизации. Суммарный заряд белковой молекулы зависит от соотношения ионизированных анионных радикалов Глу и Асп и катионных радикалов Лиз, Apr и Гис. Степень ионизации функциональных групп этих радикалов зависит от рН среды. При рН раствора около 7 все ионогенные группы белка находятся в ионизированном состоянии. В кислой среде увеличение концентрации протонов (Н+) приводит к подавлению диссоциации карбоксильных групп и уменьшению отрицательного заряда белков: -СОО- + Н+ → -СООН. В щелочной среде связывание избытка ОН" с протонами, образующимися при диссоциации NH3+с образованием воды, приводит к уменьшению положительного заряда белков: -NH3+ +ОН- → -NH2 + H2O. Значение рН, при котором белок приобретает суммарный нулевой заряд, называют "изоэлектрическая точка" и обозначают как pI. В изоэлектрической точке количество положительно и отрицательно заряженных групп белка одинаково, т.е. белок находится в изоэлектрическом состоянии. Изоэлектрическая точка (pI) — кислотность среды (pH), при которой определённая молекула или поверхность не несёт электрического заряда. Амфотерные молекулы (цвиттер-ионы) содержат как положительные, так и отрицательные заряды, наличием которых определяется pH раствора. Заряд различных функциональных групп таких молекул может меняться в результате связывания или, наоборот, потери протонов H+. Величина изоэлектрической точки такой амфотерной молекулы определяется величинами констант диссоциации кислотной и осно́вной фракций:
50.Осаждение ВМС. Обратимое и необратимое осаждение. Денатурация белка. Определение и механизм. Денатурация белков — термин биологической химии, означающий потерю белками их естественных свойств (растворимости, гидрофильности и др.) вследствие нарушения пространственной структуры их молекул. Механизмы денатурации Практически любое заметное изменение внешних условий, например, нагревание или обработка белка кислотой приводит к последовательному нарушению четвертичной, третичной и вторичной структур белка. Обычно денатурация вызывается повышением температуры, действием сильных кислот и щелочей, солей тяжелых металлов, некоторых растворителей (спирт), радиации и др. Денатурация часто приводит к тому, что в коллоидном растворе белковых молекул происходит процесс агрегации частиц белка в более крупные. Визуально это выглядит, например, как образование «белка» при жарке яиц. Ренатурация (высаливание) — процесс, обратный денатурации, при котором белки возвращают свою природную структуру. Нужно отметить, что не все белки способны ренатурировать; у большинства белков денатурация необратима.
52.Вязкость растров ВМС. Уравнение Штаудингера. Опишите закон Ньютона При формулировке законов Ньютона важно различать два связанных с ним утверждения: определение инерциальной системы отсчета и непосредственно сам закон природы. Определения по своей сути представляют собой утверждения, поясняющие смысл тех или иных терминов и вводятся в результате общепринятых соглашений о их употреблении. Первый закон Ньютона постулирует наличие такого явления, как инерция тел. Поэтому он также известен как Закон инерции. Инерция — это явление сохранения телом скорости движения (и по величине, и по направлению), когда на тело не действуют никакие силы. Чтобы изменить скорость движения, на тело необходимо подействовать с некоторой силой. Второй закон — дифференциальный закон движения, описывающий взаимосвязь между приложенной к материальной точке силой и получающимся от этого ускорением этой точки. Фактически, второй закон Ньютона вводит массу как меру проявления инертности материальной точки в выбранной инерциальной системе отсчёта (ИСО) Закон:В инерциальной системе отсчёта ускорение, которое получает материальная точка, прямо пропорционально равнодействующей всех приложенных к ней сил и обратно пропорционально её массе. Третий закон Ньютона. Этот закон объясняет, что происходит с двумя взаимодействующими телами. Возьмём для примера замкнутую систему, состоящую из двух тел. Первое тело может действовать на второе с некоторой силой Закон: Материальные точки попарно действуют друг на друга с силами, имеющими одинаковую природу, направленными вдоль прямой, соединяющей эти точки, равными по модулю и противоположными по направлению:
Опишите закон Эйнштейна. Важнейшим из таких отличий является закон Эйнштейна, связывающий массу тела с его энергией: масса тела пропорциональна его полной энергии, или обратно: полная энергия тела пропорциональна его массе.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2586; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 13.59.67.189 (0.007 с.) |



 , а второе — на первое с силой
, а второе — на первое с силой  . Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
. Как соотносятся силы? Третий закон Ньютона утверждает: сила действия равна по модулю и противоположна по направлению силе противодействия. Подчеркнём, что эти силы приложены к разным телам, а потому вовсе не компенсируются.
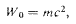 (200.1)
(200.1)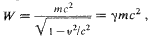 (200.2)
(200.2)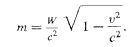
 (200.3)
(200.3)