
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Применение модифицированного критерия КолмогороваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1. Используя упорядоченные массивы хi~N(5,1) и Fn(хi) = · Вычислите значения оценки СКО и среднего арифметического для исходной выборки в отдельных ячейках, используя стандартные статистические функции (см. работу № 1). · zi для распределения, характеризуемого средним и стандартным отклонением по формуле (3.2). · Значения функции распределения вероятностей F вычислите с помощью функции НОРМРАСП (x;среднее;СКО;1), которая возвращает нормальную функцию распределения для указанного среднего и СКО. Последний аргумент определяет вид функции: 1 означает, что функция НОРМРАСП возвращает интегральную функцию распределения; 0 –возвращается функция плотности распределения. Уравнение для плотности нормального распределения имеет вид:
· Вычислите абсолютные значения отклонений эмпирической функции распределения от теоретической 2. Вычислите
3. Наконец найдите значение модифицированного критерия Колмогорова (3.5). Если выполняется условие Использование критерия согласия 1. Для проверки закона распределения по критерию согласия Пирсона постройте данные в виде табл. 3.2. Таблица 3.2
2. Заполните столбец 1, автоматическим заполнением ячеек. 3. В ячейки столбца 2 внесите ссылки на ячейки столбца значений границ интервалов, расположенных на листе построения гистограммы относительных частот. Число значений в интервале равно соответствующей частоте попадания значений вариационного ряда в интервал[7]. 4. Вычислите значения теоретической вероятности (столбец 5): · Вычислите для каждой границы интервала ее нормированное значение · Используя полученные значения в качестве аргумента, вычислите теоретическую интегральную функцию нормированного нормального распределения
· Далее по формуле (3.8) вычислите значения теоретической вероятности 5. Заполните столбец 6, предварительно вычислив объем выборки · Постройте график зависимости 6. Отдельно вычислите значение статистики критерия согласия Пирсона по формуле (3.7), предварительно заполнив ячейки столбца 7. Вычисленное значение 7. Для вычисления уровня значимости наблюденного значения статистики
где Решите обе задачи использования критерия Пирсона: п.6 и п.7. Сравните результаты вычислений.
5. Контрольные вопросы 1. В чем заключается метод линеаризации интегральной функции распределения проверки гипотезы о виде закона распределения? 2. Что такое статистические критерии? 3. Что показывает уровень значимости статистического критерия? 4. Как используется критерий Колмогорова? 5. Как используется критерий согласия Пирсона? 6. Что делать если при объеме выборки 20 критерий Колмогорова и Пирсона дают противоречивые результаты?
ЛАБОРАТОРНАЯ РАБОТА № 4 Цель работы Изучить основные особенности и методы объединения результатов разных серий измерений в общий массив значений.
Задание Выполнить объединение двух выборок разного объема из одной генеральной совокупности при отсутствии систематических ошибок и нормальном законе распределения случайных ошибок измерений, используя двухвыборочный t-критерий.
Краткая теория Предположим, что измерительную информацию о некоторой физической величине постоянного размера получают сериями – в разное время, в разных условиях, разными методами, разные операторы. Если объединить все результаты измерений в общий массив, то можно было бы получить более точный и надежный результат за счет увеличения объема выборки. Однако такое объединение возможно только при условии, что вид закона распределения (например, нормальный) обеих выборок один и тот же и математические ожидания у них равны (дисперсии могут быть различны). В математической статистике однородными называются серии (выборки), взятые из одной генеральной совокупности, то есть имеющие одинаковый вид закона распределения, одинаковые математические ожидания и одинаковые дисперсии. В метрологии однородные серии могут иметь различные дисперсии [2]. Если дисперсии в сериях одинаковы (не выборочные их оценки, а сами дисперсии), то в простейшем случае для двух серий измерений критерий однородности (t-критерий) имеет вид [4, 5, 7, 8, 11]:
где
где Прежде чем воспользоваться критерием (4.1), необходимо убедиться, что
где Если условие (4.3) выполняется, гипотеза о равенстве дисперсий принимается на уровне значимости Если условия (4.3) и (4.1) выполняются, делается вывод о равноточности и однородности серий. В этом случае все экспериментальные данные объединяются и обрабатываются как единый массив, для которого вычисляются оценки основных статистических параметров:
Поскольку для серий оценки
где Критериями (4.1) и (4.3) можно пользоваться и тогда, когда число серий больше двух, но
При построении t-интервала для истинного значения в случае объединения равноточных серий берут число степеней свободы
Ход работы 1. Получите n1i и n2i из N(5;1), – две серии случайных чисел, распределенных по нормальному закону, с математическим ожиданием равным 5, и дисперсией 1 (для этого выполните шаги п.2 или п.3, лабораторной работы № 1). Размерность серий может быть произвольной, необязательно одинаковой. 2. Выполните расчет двухвыборочного F-теста для дисперсий, используя одноименный инструмент надстройки Анализ данных (см. рис. 4.1). Примерный вид результатов работы надстройки «Двухвыборочный
Рис. 4.1. Двухвыборочный F-тест для дисперсий
3. Проверьте гипотезу
Рис. 4.2. Примерный результат расчета F-теста
· Число степеней свободы (показатель df) рассчитывается в ячейках В35 и С35 по формулам =В34-1 и =С34-1 соответственно. · Значение критерия F вычисляется в ячейке В36 по формуле =В33/С33, где в ячейках В33 и С33 рассчитываются оценки дисперсии с помощью функции ДИСП (сведения о функции ДИСП см. в лаб. работе № 1). Это соответствует формуле (4.3). В случае, когда при расчете двухвыборочного F-теста для дисперсий в качестве интервала переменной 1 (рис. 4.1) выбирается выборка с меньшей дисперсией, то для соответствия с формулой (4.3) необходимо найти значение F, обратное вычисленному в ячейке В36. · Значение Р(F<=f) показывает уровень значимости, при котором значение F становится критическим. · Значение показателя F критическое одностороннее определяется в ячейке В38 по формуле = FРАСПОБР (1-0,05;В35;С35), которая рассчитывает обратное F-распределение. Функция используется в ситуациях, когда известен уровень надежности (или уровень значимости) и необходимо рассчитать значение F-критерия. Первый аргумент – вероятность, соответствующая двустороннему F-распределению (уровень значимости
· Можно получить двустороннюю оценку Fкр., используя функцию FРАСПОБР при уровне значимости · Сравните расчетное значение F с параметром F критическое одностороннее по формуле (4.3), если F£ Fкр., гипотеза · Для расчета значения параметра Р(F<=f) одностороннее в ячейке В37 (рис.4.2) можно использовать следующие функции, родственные режиму «Двухвыборочный F-тест для дисперсий». Функция FРАСП Синтаксис: FРАСП (х; степени_свободы1; степени_свободы2) Рассчитывает значение вероятности F-распределения (распределения Фишера). Х – значение, для которого вычисляется F-распределение. Степени_свободы1 – число степеней свободы для первой выборки n1. Степени_свободы2 – число степеней свободы для второй выборки n2. Замечания: · если какой-либо аргумент не является числом, то функция FРАСП возвращает значение ошибки #ЗНАЧ!; · если аргумент степени_свободы1 или степени_свободы2 не целое число, то оно усекается; · если аргумент степени_свободы1 или степени_свободы2 меньше 1 или больше 1010, то функция FРАСП возвращает значение ошибки #ЧИСЛО!. Распределение Фишера (оно иногда называется распределением Снедекора, Снедекора–Фишера, Фишера–Снедекора или распределением дисперсионного отношения) – это распределение случайной величины в виде отношения двух независимых случайных величин
распределение Фишера со степенями свободы Функция ФТЕСТ Синтаксис: ФТЕСТ (массив1; массив2) Рассчитывает для двух выборочных массивов данных двустороннее Замечания: · аргументы должны быть числами или именами, массивами или ссылками, содержащими числа; · если аргумент, который является массивом или ссылкой, содержит текстовые значения или пустые ячейки, то такие значения игнорируются; однако ячейки с нулевыми значениями учитываются; · если количество точек данных в аргументе массив1 или массив2 меньше 2 или если дисперсия аргумента массив1 или массив2 равна 0, то функция ФТЕСТ возвращает значение ошибки #ДЕЛ/0!. Для наших данных (рис. 5.2) Р(F<=f) одностороннее в ячейке В77 рассчитывается по формуле = ФТЕСТ (A43:B62;C43:C67)/2[8], которая оказывается адекватна формуле = FРАСП (F49;F48;G48)[9]. 4. Если дисперсии в сериях одинаковы, проверим однородность серий по формуле (4.1). Для этого воспользуемся режимом «Двухвыборочный
Рис. 4.3. Двухвыборочный t-тест c одинаковыми дисперсиями
Таблица значений, рассчитанных с использованием надстройки «Двухвыборочный t-тест с одинаковыми дисперсиями» представлена на рис. 4.4.
Рис. 4.4. Таблица расчетных значений двухвыборочного t-теста
5. Проверьте однородность (гипотезу · Значения Среднего (ячейки В47 и С47), Дисперсии (ячейки В48 и С48) рассчитываются с помощью соответствующих функций, описанных в лаб. работе № 1. · Объединенная оценка дисперсии (ячейка В50) рассчитывается по формуле (4.2). В синтаксисе Excel формула примет следующий вид: =((B49-1)*B48+(C49-1)*C48)/(B49+C49-2). · Число степеней свободы (показатель df) рассчитывается в ячейке В52 по формуле =B49+C49-2 как и полагается для · Основной показатель данной надстройки t-статистика вычисляется согласно формуле (4.1). В синтаксисе Excel формула примет следующий вид: = ABS (B47-C47)/ КОРЕНЬ (B50*(1/ СЧЁТ (A3:A27)+1/ СЧЁТ (B3:B25))) Здесь значения функций, применяемых в формуле интуитивно понятны. В случае сомнений см. Справочную систему Excel. Диапазоны A3:A27 и B3:B25 содержат значения первой и второй выборок соответственно. · Модуль значения t критического двустороннего вычисляется в ячейке В57 по формуле = СТЬЮДРАСПОБР (0,05;B52). Сведения по функции СТЬЮДРАСПОБР можно найти в лаб. работе № 2. · Для расчета значения одностороннего (ячейка В54) и двустороннего (ячейка В56) Функция ТТЕСТ Синтаксис: ТТЕСТ (массив1; массив2; хвосты; тип) Возвращает вероятность, соответствующую критерию Стьюдента. Функция ТТЕСТ используется, чтобы определить, насколько вероятно, что две выборки взяты из генеральных совокупностей, которые имеют одно и то же среднее. Массив1 – первое множество данных. Массив2 – второе множество данных. Хвосты – число хвостов распределения. Если хвосты = 1, то функция ТТЕСТ использует одностороннее распределение. Если хвосты = 2, то функция ТТЕСТ использует двустороннее распределение. Тип – вид исполняемого t-теста.
Замечания: · Если массив1 и массив2 имеют различное число точек данных, а тип = 1 (парный), то функция ТТЕСТ возвращает значение ошибки #Н/Д. · Аргументы хвосты и тип усекаются до целых. · Если хвосты или тип не является числом, то функция ТТЕСТ возвращает значение ошибки #ЗНАЧ!. · Если хвосты имеет значение, отличное от 1 и 2, то функция ТТЕСТ возвращает значение ошибки #ЧИСЛО!. Для случая равных дисперсий P(T<=t) одностороннее (ячейка В54 = ТТЕСТ (A3:A27;B3:B25;1;2), которая адекватна формуле = СТЬЮДРАСП (B53;B52;1), а P(T<=t) двустороннее (ячейка В56 рис. 4.4) вычисляется по формуле = ТТЕСТ (A3:A27;B3:B25;2;2), которая адекватна формуле = СТЬЮДРАСП (B53;B52;2). Функция СТЬЮДРАСП возвращает вероятность для t-распределения Стьюдента, а численное значение (аргумент В53) – это вычисленное значение, для которого должны быть вычислены вероятности. Данную функцию можно использовать вместо таблицы критических значений t-распределения. · Сравните значение t-статистики = 0,455858321612874 с t критическим односторонним или двусторонним. Для выполнения гипотезы 6. После объединения однородных серий результатов измерений выполните расчет основных статистических параметров, используя, например, режим «Описательная статистика» (см. лаб. работу № 1). 7. Постройте доверительный интервал для оценки математического ожидания объединенной выборки. Сравнить со значениями, вычисленными в лабораторной работе № 1.
5. Контрольные вопросы 1. Какие выборки называются однородными? 2. Какие значения основных статистических параметров должны иметь однородные выборки? 3. Как выполняется проверка гипотезы о равенстве дисперсий? 4. Как выполняется проверка гипотезы о равенстве математических ожиданий? 5. В каком случае можно объединять две выборки?
ЛАБОРАТОРНАЯ РАБОТА № 5 Цель работы Изучить основные особенности и методы объединения результатов разных серий измерений в общий массив значений.
Задание Выполнить объединение двух выборок разного объема из разных нормальных совокупностей с одинаковым математическим ожиданием и разной дисперсией, используя приближенный двухвыборочный t-критерий.
Краткая теория В предыдущей работе была рассмотрена процедура проверки гипотезы о равенстве средних (математических ожиданий) двух нормальных распределений с неизвестными дисперсиями. При этом делалось предположение о равенстве дисперсий между собой. Если при анализе результатов измерений была обнаружена неравноточность серий (условие (4.3) работы № 4 не выполнено), то гипотезу о равенстве математических ожиданий можно проверить по приближенному критерию:
где
Статистика t в выражении (5.1) подчиняется распределению Беренса-Фишера, пользование которым весьма затруднительно из-за отсутствия нужных таблиц и сложности процедуры пользования имеющимися. Приближенное выражение (5.2) позволяет пользоваться таблицами t-распределения.
Если обнаружена неравноточность измерений в сериях, но серии однородны по условию (5.1), при совместной их обработке неравноточность учитывается при расчете среднего арифметического введением весов
где Из курса теории вероятностей известно, что случайная величина в виде суммы двух случайных нормальных величин имеет также нормальное распределение. Однако в данном случае нельзя говорить о сумме случайных величин. Мы имеем дело со смесью двух распределений, нормальных, но с разными параметрами. Закон распределения такой смеси идентифицировать нельзя – он зависит от объемов выборок и от параметров обоих распределений. Чтобы убедиться в этом, можно построить гистограмму для объединенного массива для заметно различающихся объемов выборок, дисперсий или математических ожиданий (последнее наиболее наглядно покажет правильность нашего утверждения). По этой причине оценивание математического ожидания доверительным интервалом Стьюдента будет весьма приближенным. По этой же причине мы не рекомендуем вычислять оценку СКО для объединенного массива как не имеющую смысла при неизвестном законе распределения. Наконец, по этой же причине в метрологии при объединении неравноточных результатов обычно ограничиваются указанием значения Интервал Чебышева – интервал вероятности для случайной величины, распределенной по любому закону, но с конечными математическим ожиданием и дисперсией, имеет вид (в качестве случайной величины используем общее среднее):
Поскольку
при доверительной вероятности 0.90 (напомним, что для конкретного численного доверительного интервала следует говорить «при надежности 0.90»).
Ход работы 1. Получите n1i~N(5;4) и n2i~N(5;1), – две серии случайных чисел, распределенных по нормальному закону, с математическим ожиданием равным 5, и дисперсиями равными 4 и 1 соответственно (для этого выполните шаги п.2, лабораторной работы № 1). Размерность серий может быть произвольной, необязательно одинаковой. 2. Выполните расчет двухвыборочного F-теста для дисперсий, используя одноименный инструмент надстройки Анализ данных (см. рис. 4.1 лаб. работы № 4). Таблица результатов работы надстройки «Двухвыборочный F-тест для дисперсий» для данной работы представлена на рис. 5.1.
Рис. 5.1. Таблица результатов расчета F-теста
Обратите внимание, что в качестве Интервала переменной1 выбрана серия с большим значением оценки дисперсии, а в качестве Интервала переменной2 – с меньшей. 3. Проверьте гипотезу
Основное описание работы F-теста приведено в лаб. работе № 4. · По формулам, описанным в предыдущей лаб. работе, получены следующие двусторонние критические значения (см. рис. 5.1) · Однако и в случае двусторонних оценок значение критерия F принадлежит правому критическому интервалу, следовательно, гипотеза 4. Сравните расчетное значение F с параметром F критическое одностороннее по формуле (4.3), если F ³ Fкр., гипотеза · В случае, если в качестве Интервала переменной1 указана серия с меньшим значением оценки дисперсии, то тогда для расчетного значения F и F критического одностороннего необходимо найти их обратные значения, которые и необходимо сравнивать по формуле (4.3). Для вычисления F критического одностороннего также подходит формула = FРАСПОБР (0,05;G48;F48), где ячейки F48 и G48 содержат значения соответствующего числа степеней свободы выборок. 5. Выполните проверку однородности (гипотезу
Рис. 5.2. Таблица результатов расчета t-теста
· Число степеней свободы (показатель df) рассчитывается в ячейке F64 по формуле (5.2). В синтаксисе Excel это выражение запишется так: =((F61/F62+G61/G62)^2/((F61/F62)^2/(F62+1)+(G61/G62)^2/(G62+1))-2) После этого полученное значение округляется в меньшую сторону функцией ОКРУГЛВНИЗ до целого, для чего вторым аргументом записывается нуль. · Основной показатель данной надстройки t-статистика вычисляется согласно формуле (5.1). В синтаксисе Excel формула примет следующий вид: = ABS (F60-G60)/ КОРЕНЬ (F61/F62+G61/G62) Здесь значения функций, применяемых в формуле интуитивно понятны. В случае сомнений см. Справочную систему Excel. · Модуль значения t критического двустороннего вычисляется в ячейке F69 по формуле = СТЬЮДРАСПОБР (0,05;F64). Сведения по функции СТЬЮДРАСПОБР можно найти в лаб. работе № 2. · Для расчета значения одностороннего (ячейка F66) и двустороннего (ячейка F68) Для случая различных дисперсий P(T<=t) одностороннее (ячейка F66 рис. 5.2) вычисляется по формуле = СТЬЮДРАСП (F65;F64;1). Сравните полученное значение с вычисленным по формуле = ТТЕСТ (A43:A62;C43:C67;1;3), для неокругленного числа степеней свободы. Значение P(T<=t) двустороннего (ячейка F68 рис. 5.2) вычисляется по формуле = СТЬЮДРАСП (F65;F64;2). Сравните полученное значение с вычисленным по формуле = ТТЕСТ (A43:A62;C43:C67;2;3), для неокругленного числа степеней свободы. · Сравните значение t-статистики с t критическим односторонним или двусторонним. Для принятия гипотезы
6. Для объединения однородных неравноточных серий результатов измерений выполните расчет основных статистически параметров, используя формулы (5.3). 7. Постройте доверительный интервал для оценки математического ожидания объединенной выборки по формуле (5.4). Сравните со значениями, вычисленными в лабораторной работе № 1. 8. Постройте гистограмму частот с равным шагом, как описано в работе 2. Сравните свою гистограмму с гистограммами других студентов, сделайте вывод.
5. Контрольные вопросы 1. В каком случае нельзя объединять две выборки данных? 2. Почему закон распределения объединенного массива неравноточных выборок оказывается отличным от нормального? 3. Какой доверительный интервал для математического ожидания шире – Стьюдента или Чебышева и по какой причине? 4. Предположим, Вы по объединенному массиву проверили гипотезу о нормальности распределения и не отвергли ее. Каким доверительным интервалом для математического ожидания Вы воспользуетесь?
ЛАБОРАТОРНАЯ РАБОТА № 6 Цель работы Изучить основные особенности и методы построения линейного приближения экспериментальных данных.
Задание Методом наименьших квадратов построить линейную эмпирическую зависимость по опытным данным. Выполнить проверку адекватности математической модели опытным данным с помощью статистических критериев. Оценить погрешность эмпирической зависимости совместными доверительными F-интервалами.
Краткая теория Метод наименьших квадратов Одновременные измерения двух или более разнородных физических величин с целью нахождения зависимости между ними называются совместными измерениями [2]. Обычно выполняется
Параметры
|
|||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 671; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.219.150.195 (0.015 с.) |

 , вычислите значения функции распределения вероятностей F(хi,
, вычислите значения функции распределения вероятностей F(хi,  ,
,  ):
): .
. в отдельном столбце (диапазон N4:N28) и найдите максимальное из них
в отдельном столбце (диапазон N4:N28) и найдите максимальное из них 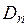 (3.3), используя функцию МАКС (N4:N28).
(3.3), используя функцию МАКС (N4:N28). для выбранного уровня значимости
для выбранного уровня значимости  приближенным выражением
приближенным выражением .
. гипотеза о нормальности отвергается, в противном случае гипотеза принимается.
гипотеза о нормальности отвергается, в противном случае гипотеза принимается.



 по формуле (3.2). Для этого воспользуйтесь функцией НОРМАЛИЗАЦИЯ (х;среднее;СКО) (столбец 4 табл. 3.2).
по формуле (3.2). Для этого воспользуйтесь функцией НОРМАЛИЗАЦИЯ (х;среднее;СКО) (столбец 4 табл. 3.2). . Функция Excel НОРМРАСП. Значения аргументов: среднего = 0, оценка СКО = 1, так как значения границ уже нормированы.
. Функция Excel НОРМРАСП. Значения аргументов: среднего = 0, оценка СКО = 1, так как значения границ уже нормированы. .
. (функция СЧЕТ). Для контроля правильности вычислений выполните суммирование значений ячеек столбца 6 – результат должен быть немного меньше 1 (см. раздел 3, п. «Построение гистограммы» лабораторной работы № 2).
(функция СЧЕТ). Для контроля правильности вычислений выполните суммирование значений ячеек столбца 6 – результат должен быть немного меньше 1 (см. раздел 3, п. «Построение гистограммы» лабораторной работы № 2). сравнивается с табличным (критическим) при выбранном одностороннем уровне значимости
сравнивается с табличным (критическим) при выбранном одностороннем уровне значимости  . Если
. Если  , то гипотеза о виде распределения принимается. Критическое значение статистики критерия можно вычислить с помощью функции ХИ2РАСП (x;степени_свободы), которая возвращает одностороннюю вероятность распределения
, то гипотеза о виде распределения принимается. Критическое значение статистики критерия можно вычислить с помощью функции ХИ2РАСП (x;степени_свободы), которая возвращает одностороннюю вероятность распределения  . х – это значение, для которого требуется вычислить распределение. В нашем случае это значение статистики критерия согласия Пирсона, вычисленное по формуле (3.7). Степени_свободы – это число степеней свободы.
. х – это значение, для которого требуется вычислить распределение. В нашем случае это значение статистики критерия согласия Пирсона, вычисленное по формуле (3.7). Степени_свободы – это число степеней свободы. , при котором значение критерия становится критическим, можно воспользоваться методом интерполяции табличных значений
, при котором значение критерия становится критическим, можно воспользоваться методом интерполяции табличных значений  ,
, .
. , (4.1)
, (4.1) и
и  – средние арифметические в сериях;
– средние арифметические в сериях;  и
и  – объемы серий;
– объемы серий;  – табличное значение t-статистики;
– табличное значение t-статистики;  – объединенная оценка дисперсии
– объединенная оценка дисперсии  :
: , (4.2)
, (4.2) и
и  – выборочные оценки дисперсии в сериях;
– выборочные оценки дисперсии в сериях;  – число степеней свободы оценки
– число степеней свободы оценки  и
и  есть оценки одной и той же дисперсии
есть оценки одной и той же дисперсии  в виде выражения (4.2). Проверка гипотезы о равенстве дисперсий в сериях при нормальном распределении осуществляется с помощью F-критерия (критерия дисперсионного отношения) [4, 5, 7, 8, 11]:
в виде выражения (4.2). Проверка гипотезы о равенстве дисперсий в сериях при нормальном распределении осуществляется с помощью F-критерия (критерия дисперсионного отношения) [4, 5, 7, 8, 11]: , (4.3)
, (4.3) – максимальная из двух оценок
– максимальная из двух оценок  – число степеней свободы числителя (
– число степеней свободы числителя ( );
);  – минимальная из двух оценок,
– минимальная из двух оценок,  – число степеней свободы знаменателя. Значение
– число степеней свободы знаменателя. Значение  берется из таблиц F-распределения при одностороннем уровне значимости
берется из таблиц F-распределения при одностороннем уровне значимости  . (4.4)
. (4.4) и
и  обычно бывают уже вычислены, то удобнее пользоваться другими формулами. Для двух серий они имеют вид
обычно бывают уже вычислены, то удобнее пользоваться другими формулами. Для двух серий они имеют вид , (4.5)
, (4.5) – общее число данных объединенного массива.
– общее число данных объединенного массива. в сериях приблизительно одинаковы. Если серии с максимально различающимися
в сериях приблизительно одинаковы. Если серии с максимально различающимися  .
.
 =
=  о равенстве дисперсий в сериях n1 и n2 по таблице значений параметров надстройки «Двухвыборочный
о равенстве дисперсий в сериях n1 и n2 по таблице значений параметров надстройки «Двухвыборочный 
 0,025. Тогда формула = FРАСПОБР
0,025. Тогда формула = FРАСПОБР = 0,43555736, а формула = FРАСПОБР (0,025; В35; С35) – значение правосторонней критической точки
= 0,43555736, а формула = FРАСПОБР (0,025; В35; С35) – значение правосторонней критической точки  = 2,331503879. Таким образом, при двусторонней оценке получим критическую область как объединение двух интервалов
= 2,331503879. Таким образом, при двусторонней оценке получим критическую область как объединение двух интервалов  . Однако и в случае двусторонних оценок значение критерия F не принадлежит ни одному критическому интервалу, следовательно, гипотеза
. Однако и в случае двусторонних оценок значение критерия F не принадлежит ни одному критическому интервалу, следовательно, гипотеза  принимается.
принимается. также принимается.
также принимается. , каждая из которых имеет распределение
, каждая из которых имеет распределение  , где
, где  – число степеней свободы. Связь между
– число степеней свободы. Связь между  -распределением и распределением
-распределением и распределением  , таким образом, дается формулой:
, таким образом, дается формулой: .
. . На практике чаще применяется функция FРАСПОБР.
. На практике чаще применяется функция FРАСПОБР.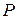 -значение F-теста. Массив1 – первая выборка данных. Массив2 – вторая выборка данных.
-значение F-теста. Массив1 – первая выборка данных. Массив2 – вторая выборка данных.

 о равенстве математических ожиданий) серий измерений по таблице значений параметров надстройки «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 4.4).
о равенстве математических ожиданий) серий измерений по таблице значений параметров надстройки «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 4.4). -значения t-теста можно использовать функцию ТТЕСТ, родственную режиму «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 4.4).
-значения t-теста можно использовать функцию ТТЕСТ, родственную режиму «Двухвыборочный t-тест с одинаковыми дисперсиями» (рис. 4.4).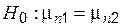 критическая область образуется объединением интервалов
критическая область образуется объединением интервалов  . Так как условие (4.1) выполняется, т.е. значение t-статистики не попадает ни в один критический интервал, то гипотезу
. Так как условие (4.1) выполняется, т.е. значение t-статистики не попадает ни в один критический интервал, то гипотезу  о равенстве математических ожиданий принимаем.
о равенстве математических ожиданий принимаем. , (5.1)
, (5.1) . (5.2)
. (5.2) , а вычисления выполняются по формулам:
, а вычисления выполняются по формулам: (5.3)
(5.3) выборочные средние,
выборочные средние,  общее среднее (среднее арифметическое объединенных серий),
общее среднее (среднее арифметическое объединенных серий),  выборочные оценки дисперсии.
выборочные оценки дисперсии. . Можно воспользоваться интервалом Чебышева, хотя скорее всего он будет излишне широким.
. Можно воспользоваться интервалом Чебышева, хотя скорее всего он будет излишне широким.
 неизвестна, воспользуемся ее оценкой по последней формуле из (5.3). Задавшись вероятностью, например, 0.90, мы приближенно получим
неизвестна, воспользуемся ее оценкой по последней формуле из (5.3). Задавшись вероятностью, например, 0.90, мы приближенно получим  откуда приближенный доверительный интервал Чебышева примет вид:
откуда приближенный доверительный интервал Чебышева примет вид: (5.4)
(5.4)
 о равенстве дисперсий в сериях n1 и n2 по таблице значений параметров надстройки «Двухвыборочный F-тест для дисперсий» (рис. 5.1).
о равенстве дисперсий в сериях n1 и n2 по таблице значений параметров надстройки «Двухвыборочный F-тест для дисперсий» (рис. 5.1). .
. не принимается.
не принимается. о равенстве математических ожиданий) серий измерений по таблице значений параметров надстройки «Двухвыборочный t-тест с различными дисперсиями» (рис. 5.2). Значения Среднего (ячейки F60 и G60), Дисперсии (ячейки F61 и G61) рассчитываются с помощью соответствующих функций, описанных в лаб. работе № 1.
о равенстве математических ожиданий) серий измерений по таблице значений параметров надстройки «Двухвыборочный t-тест с различными дисперсиями» (рис. 5.2). Значения Среднего (ячейки F60 и G60), Дисперсии (ячейки F61 и G61) рассчитываются с помощью соответствующих функций, описанных в лаб. работе № 1.
 . Так как условие (5.1) выполняется, а также значение t-статистики не попадает ни в один критический интервал, то гипотезу
. Так как условие (5.1) выполняется, а также значение t-статистики не попадает ни в один критический интервал, то гипотезу 
 . Задача состоит в том, чтобы по
. Задача состоит в том, чтобы по  ,
,  ) построить зависимость (эмпирическую), которая была бы несмещенной и эффективной оценкой истинной зависимости, общий вид которой считают известным. Например, известно, что истинная зависимость есть прямая линия, представленная в виде
) построить зависимость (эмпирическую), которая была бы несмещенной и эффективной оценкой истинной зависимости, общий вид которой считают известным. Например, известно, что истинная зависимость есть прямая линия, представленная в виде . (6.1)
. (6.1) ,
,  неизвестны, их следует оценить по опытным данным. Будем считать ошибки измерений
неизвестны, их следует оценить по опытным данным. Будем считать ошибки измерений  случайными с нулевым математическим ожиданием и дисперсией
случайными с нулевым математическим ожиданием и дисперсией 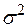 при любом
при любом 


