
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистическая проверка адекватности моделиСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Все приведенные выше выражения справедливы при выполнении предположения о том, что истинный вид зависимости заранее известен, причем эта зависимость линейна по искомым параметрам. Если же это не так, что обычно и имеет место, то утверждение о несмещенности оценок Известный F-критерий проверки адекватности модели опытным данным использует статистику в виде отношения остаточной дисперсии
На практике исследователь часто не имеет в своем распоряжении независимой несмещенной оценки дисперсии опытных данных и не может воспользоваться критерием (6.9). В этом случае можно воспользоваться следующим критерием:
Этот критерий использует статистику в виде отношения двух последовательных по числу параметров модели остаточных дисперсий; здесь, как обычно, число степеней свободы Линейному регрессионному анализу посвящено множество работ разной сложности, из которых отметим [6, 12, 13, 14]. Наиболее доступно он изложен в [5, 6]. Оценивание погрешности эмпирической зависимости Погрешность – это некий интервал, построенный в обе стороны от результата измерений и включающий в себя ("накрывающий") неизвестное истинное значение измеряемой физической величины с высокой вероятностью (с заданной или оцененной). Имея оценку СКО эмпирической зависимости (6.8), можно при каждом значении аргумента Погрешность эмпирической зависимости будем выражать совместными доверительными интервалами [12, 5], например, F-интервалами Шеффе, которые проще всего вычислить (они имеют и более серьезные преимущества по сравнению с другими совместными интервалами). Интервалы Шеффе имеют вид:
где
Ход работы 1. Для построения регрессионной прямой по методу наименьших квадратов можно воспользоваться двумя подходами: 1) решить систему линейных алгебраических уравнений, корнями которой будут коэффициенты · Вычислите вспомогательные суммы xi, yi, xi^2, yi*xi (функция СУММ (диапазон_значений) или кнопка на палитре инструментов со знаком 'сигма'), а также подсчитайте количество точек данных (функция СЧЕТ (диапазон_значений)). Составьте матрицу из полученных значений согласно формулам метода наименьших квадратов. · Для вычисления корней системы можно 1) найти обратную матрицу (функция МОБР (массив), при том надо помнить следующее, для того чтобы получить матрицу необходимо сначала выделить тот диапазон ячеек, в которых предполагается получить значения элементов обратной матрицы, затем ввести функцию в строке формул, и, наконец, нажать комбинацию клавиш CTRL+SHIFT+ENTER. Если нажать одну клавишу ENTER, то Excel вычислит только первый элемент матрицы. Это относится ко всем функциям массива Excel). Умножить обратную матрицу на столбец свободных членов (функция МУМНОЖ (массив1; массив2). Это также функция массива). В результате получаются коэффициенты прямой. 2) по методу Крамера вычислить определители системы и вспомогательные определители переменных (функция МОПРЕД (матрица) – для получения результата достаточно нажать ENTER). Затем вычислить корни системы – коэффициенты прямой. 2. Для реализации второго подхода нужно применить функцию
Функция ЛИНЕЙН Синтаксис: ЛИНЕЙН (извест_значения_y;извест_значения_x;конст; статист) Извест_значения_y – это множество значений y, которые уже известны для соотношения (6.2). Замечания: · Если массив извест_значения_y имеет один столбец, то каждый столбец массива извест_значения_x интерпретируется как отдельная переменная. · Если массив извест_значения_y имеет одну строку, то каждая строка массива извест_значения_x интерпретируется как отдельная переменная. Извест_значения_x – это необязательное множество значений x, которые уже известны для соотношения (6.2). Массив извест_значения_x может содержать одно или несколько множеств переменных. Если используется только одна переменная, то извест_значения_y и извест_значения_x могут быть массивами любой формы при условии, что они имеют одинаковую размерность. Если используется более одной переменной, то извест_значения_y должны быть вектором (то есть интервалом высотой в одну строку или шириной в один столбец). · Если извест_значения_x опущены, то предполагается, что это массив {1;2;3;...} такого же размера как и извест_значения_y. Конст – это логическое значение, которое указывает, требуется ли, чтобы константа · Если конст имеет значение ИСТИНА или опущено, то Статистика – это логическое значение, которое указывает, требуется ли вернуть дополнительную статистику по регрессии. · Если статистика имеет значение ИСТИНА, то функция ЛИНЕЙН возвращает дополнительную регрессионную статистику, так что возвращаемый массив будет иметь вид: {mn;mn-1;...;m1;b:sen;sen1;...;se1; seb:r2;sey:F;df:ssreg; ssresid}. Если статистика имеет значение ЛОЖЬ или опущена, то функция ЛИНЕЙН возвращает только коэффициенты Функция ИНДЕКС Синтаксис: ИНДЕКС (массив;номер_строки;номер_столбца) Массив – это интервал ячеек или массив констант. Номер_строки – это номер строки в массиве, из которой нужно возвращать значение. Если номер_строки опущен, то аргумент номер_столбца нужно задавать обязательно. Номер_столбца – это номер столбца в массиве, из которого нужно возвращать значение. Замечания: · Если номер_столбца опущен, то аргумент номер_строки нужно задавать обязательно. Если используются оба аргумента номер_строки и номер_столбца, то функция ИНДЕКС возвращает значение, находящееся в ячейке на пересечении номер_строки и номер_столбца. · Если массив содержит только одну строку или один столбец, то соответствующий аргумент номер_строки или номер_столбца не является обязательным. · Если массив занимает больше, чем одну строку и больше, чем один столбец, а задан только один аргумент номер_строки или номер_столбца, то функция ИНДЕКС возвращает массив из целой строки или целого столбца аргумента массив. · Если задать номер_строки или номер_столбца равным 0 (нулю), то функция ИНДЕКС вернет массив значений для целого столбца или целой строки, соответственно. Для того, чтобы использовать значения, возвращаемые как массив, функцию ИНДЕКС нужно ввести как формулу массива в горизонтальный интервал ячеек. Для ввода формулы массива нажмите клавиши CTRL+SHIFT+ENTER. Таким образом, для вычисления коэффициента = ИНДЕКС (ЛИНЕЙН (B2: B20;A2:A20);1).
Для вычисления коэффициента
= ИНДЕКС (ЛИНЕЙН (B2:B20;A2:A20);2).
Полученные по обоим способам значения коэффициентов прямой будут идентичны. 3. Постройте столбец значений регрессионной прямой, вычисленных по формуле (6.2), где х – известные значения аргумента, 4. Постройте графики исходной зависимости и МНК-прямой в одних осях (мастер диаграмм). 5. Вычислите значения оценки СКО для МНК-прямой и погрешности Dх по формуле 6. Нанесите полученные значения погрешности на тот же график. Для точек МНК-прямой в диалоговом окне Формат рядов данных показать обе планки погрешностей по Х. Сравнить с вычисленными значениями погрешностей. 7. Выполните построение МНК-прямой и вычисление различных статистических параметров с помощью категорией «Регрессия» Пакета анализа Excel. Сравните полученные результаты с результатами предыдущих пунктов работы. 5. Контрольные вопросы 1. В чем суть метода наименьших квадратов построения линейной эмпирической зависимости? Сформулируйте принцип Лежандра. 2. Что такое остаточная дисперсия? Каковы статистические характеристики остаточной дисперсии при нормальном законе распределения? 3. Какие статистические критерии используются для проверки адекватности модели опытным данным при наличии и отсутствии независимой несмещенной оценки дисперсии? 4. Что такое погрешность? Как определить погрешность эмпирической зависимости?
ЛАБОРАТОРНАЯ РАБОТА № 7 Цель работы Освоить элементарные приемы анализа таблиц сопряженности 2´2,
Задание Создать с помощью генератора случайных чисел 4 случайных двухзначных числа из равномерной совокупности и представить их в виде таблицы 2´2для некоторых условных признаков
Краткая теория Начнем с примера. В приведенной ниже табл. 1 представлены сведения о числе людей, заболевших и не заболевших холерой с указанием, была ли им сделана противохолерная прививка (пример взят из [11]).
Таблица 1
Задача состоит в том, чтобы выяснить, эффективна ли прививка, значимо ли ее влияние на вероятность заболевания. Видно, что доля заболевших среди непривитых больше, чем среди привитых, но не объясняется ли это случайными факторами? Аналогичных примеров можно привести множество – это и обработка анкет разного рода, исследований социологического, медицинского, экономического характера, иначе говоря – данных, представленных в номинальных шкалах (вместо числового значения указывается то или иное имя). Если градация признаков и групп (будем называть признаками «имена», указанные в крайнем левом столбце, а группами – указанные в верхней стоке) осуществлена по принципу «да – нет», причем суммы по нижней строке и правому столбцу совпадают, то такая таблица называется таблицей сопряженности (признаков) 2´2. Отметим, что существуют таблицы сопряженности размером В качестве нулевой гипотезы примем утверждение: прививка не оказывает заметного влияния на вероятность заболевания, а видимый эффект есть следствие случайных вариаций числа заболевших. На языке математической статистики это звучит так: вероятность заболевания для привитых и непривитых равна одному и тому же значению Замечание: Мы сильно осложнили бы свою задачу, если бы в качестве нулевой гипотезы выдвинули противоположное утверждение о значимости влияния прививки, т.к. такая гипотеза оказывается множественной (нам пришлось бы указывать, насколько сильно влияние прививки, во сколько раз или на сколько она снижает вероятность заболевания). Но вероятность Таблица 2
Критерий согласия
где
Общее число слагаемых (мы имеем двойную сумму) равно 4, а число уравнений связи равно 2 (сумма по строкам равна сумме по столбцам и равна Найдем наблюденное значение статистики критерия:
По таблице процентных точек распределения · уровню значимости 2.5 % соответствует предел · уровню значимости 1 % соответствует предел Следовательно, значение 6.07 соответствует уровню значимости Это и есть «уровень значимости нулевой гипотезы», он слишком мал, чтобы считать гипотезу верной. Опыт вынуждает нас отклонить гипотезу о том, что прививка не оказывает влияния на вероятность заболевания, и мы приходим к выводу, что прививка заметно уменьшает эту вероятность.
Ход работы 1. Создайте таблицу сопряженности размерностью 2´2. Для этого вспомните ситуацию из личного опыта о наличии (отсутствии) некоторого признака у двух групп людей (социологическое исследование). Ситуация должны быть типа «да-нет», т.е. в первой строке предполагается наличие признака, во второй – его отсутствие (см. табл. 1). · Укажите названия признаков в первом столбце таблицы и названия групп в верхней строке (если затрудняетесь, то в качестве имен укажите числительные «первая», «вторая»). · Выполните генерацию случайных чисел, распределенных по равномерному закону (см. лаб. работу № 1). Каждое полученное число умножьте на 1000 и округлите до целого (подумайте почему?) · Найдите суммы полученных значений по строкам, столбцам и общую сумму. 2. В отдельной таблице рассчитайте теоретические частоты для выбранной гипотезы · Для контроля значений теоретических частот вычислите суммы. Они должны совпадать с вычисленными в исходной таблице. 3. Вычислите значение статистики 4. По таблице процентных точек распределения
5. Контрольные вопросы 1. Какие признаки называются номинальными? 2. В каких случаях используются таблицы сопряженности признаков? 3. Какую гипотезу и почему выдвигают при обработке таблиц сопряженности? 4. На основании чего делается вывод о зависимости признаков? ЗАКЛЮЧЕНИЕ В пособии рассмотрены лишь 7 задач по обработке данных, но эти задачи являются основными и на их базе строится дальнейший, более глубокий анализ результатов измерений и наблюдений. Приведенные в них теоретические сведения довольно кратки, но их достаточно для понимания того, какие именно операции выполняет или должен выполнить компьютер. В любом случае студенту на этапе освоения пакета электронных таблиц MS Excel в части применения его к решению описанных задач, рекомендуется внимательно ознакомиться с прил. 1–3, в которых отмечены как тонкости процедур диалога с компьютером, так и типичные ошибки операторов. Полезно также контролировать правильность действий и получаемые результаты с помощью отдельных контрольных операций с использованием статистических таблиц, приведенных в прил. 4. Отметим в заключение, что хотя пакет Excel не является наилучшим статистическим пакетом, его широкое распространение в различных сферах человеческой деятельности послужили толчком к составлению данного сборника. «Цель вычислений – понимание, а не числа» (Р. Хэмминг).
ПРИЛОЖЕНИЕ 1 Установка надстройки "Пакет анализа" Для того, чтобы отыскать команду вызова надстройки Пакет анализа в Microsoft Excel, необходимо воспользоваться меню С е рвис (рис. 1). Здесь возможны следующие ситуации: 1. В меню С е рвис присутствует команда Ана л из данных… (рис. 1). Это самый простой и идеальный случай, так как достаточно щелкнуть указателем мыши, чтобы воспользоваться окном надстройки. 2. В меню С е рвис отсутствует команда Ана л из данных… В этом случае необходимо в том же меню выполнить команду Надстро й ки… В результате раскроется одноименное диалоговое окно со списком доступных надстроек (рис. 2). Среди доступных надстроек выберите элемент Пакет анализа. После этого в меню С е рвис появится соответствующая команда. Эта ситуация наиболее типична, так как надстройка Пакет анализа инсталлируется при стандартной установке.
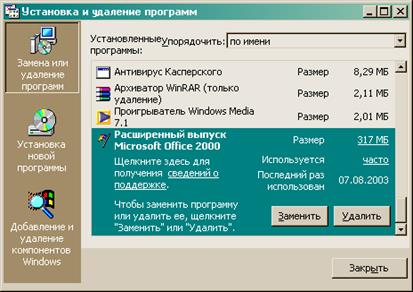
3. В меню С е рвис отсутствует команда Анализ данных…, а в списке окна Надстройки нет элемента Пакет анализа. Это самая сложная ситуация, так как без установочного комплекта MS Office не обойтись. После установки дистрибутивного компакт-диска Microsoft Office, перейдите в папку Панель управления (главное меню Пуск) – Установка и удаление программ (рис. 3). Выберите кнопку З аменить, затем следуйте инструкциям Мастера установки, выбирая те пункты и опции, которые вам необходимы. При установки надстройки Пакет анализа установите и все другие надстройки Microsoft Excel. Они значительно расширят возможности программы, а при этом займут на винчестере совсем немного места. Вид диалогового окна Установка и удаление программ может отличаться в разных операционных системах. Окончание прил. 1
Рис. 3. Диалоговое окно Установка и удаление программ
Если все сделано правильно и названия папок были оставлены по умолчанию, то в папке C:\ Program Files\ Microsoft Office\ Office\ Library\ Analysis появится файл надстройки analysis32.xll.
ПРИЛОЖЕНИЕ 2 Виды ошибок при задании формул Формула представляет собой синтаксическую конструкцию со знаком “=” в первой позиции, набирается с клавиатуры или кнопкой Формула может содержать следующие элементы: Выражение – это операнды, соединенные знаками операций. Используемые в формулах Excel операции приведены в таблице 1. Порядок вычисления выражений слева направо с учетом приоритетов операций и может быть изменен скобками (). Таблица 1 Операции в формулах Excel
Операнд – это константа, ссылка на ячейку или диапазон ячеек, заголовок, имя или функция. Константа – это число или текст, введенные с клавиатуры, в отличие от формулы или возвращаемого ею значения. Ссылка на ячейку – это адрес ячейки, однозначно определяющий ее месторасположение, в Excel по умолчанию используется стиль адресации А1 по букве столбца и номеру строки, на пересечении которых расположена ячейка. При помощи ссылок можно использовать в одной формуле данные из разных частей листа, а также использовать в нескольких формулах значение одной ячейки. При создании формул используются следующие типы ссылок. Абсолютная ссылка – фиксированный адрес ячейки на листе, например, $А$3. Абсолютные адреса предваряются знаком $. Относительная ссылка – относительно ячейки с формулой, содержащей эту ссылку, например, A3. Продолжение прил. 2 Смешанная ссылка. Например, А$1 – абсолютная ссылка на первую строку, $A1 – абсолютная ссылка на первый столбец. Ссылки на ячейки других листов той же книги, Лист2!А1. Внешние ссылки на другие книги, [Книга2]Лист1!A1 на открытую книгу, иначе с полным путем к книге на локальном диске, ‘С:\Мои документы\[Книга2]Лист1’!$A$1. Удаленные ссылки на данные других приложений; сетевые адреса и URL (Uniform Resource Locator, унифицированный указатель ресурса, Трехмерные ссылки на несколько листов, Лист2:Лист13!A1. Циклические ссылки – это последовательность ссылок, при которой формула ссылается на себя напрямую или через другие ссылки. Вычисление следующих значений по предыдущим в таких замкнутых последовательностях называется итерацией. Excel прекращает итерационный процесс по заранее установленным ограничениям на количество итераций, по умолчанию 100, или на невязку (разность значений с двух соседних итераций), по умолчанию 0,001. Ячейки, на которые есть ссылки в указанной ячейке, называются влияющими. Ячейки, в которых есть ссылки на указанную ячейку, называются зависимыми. При перемещении ячейки, ее формула не изменяется. При этом во всех зависимых ячейках ссылки всех типов выправляются на новое местоположение перемещенной ячейки. При копировании формулы абсолютные ссылки не обновляются. Относительные ссылки при копировании формулы в другую ячейку обновляются автоматически так, что взаимное расположение влияющих ячеек и формулы сохраняется. Например, формула в ячейке A3 =$A$1+A2 после копирования в ячейку В3 =$A$1+B2. Копирование формулы в примыкающий диапазон можно быстро осуществить протаскиванием маркера заполнения. Диапазон – это несколько ячеек листа. Ссылка на непрерывный прямоугольный диапазон задается как адрес левой верхней ячейки: адрес правой нижней ячейки. В ссылке на несмежный диапазон поддиапазоны перечисляются через; и выделяются на листе с нажатым Ctrl. Формула может содержать одну или несколько функций, связанных между собой арифметическими операторами или вложенных друг в друга. Функции – это встроенные в программу Excel формулы, которые выполняют вычисления по своим аргументам. Обращение к функции идет по имени функции и в скобках списку аргументов через запятую. Вставку функции можно выполнить, используя меню Вст а вка – Продолжение прил. 2
Аргумент функции – это число, текст, логическая величина, массив, значение ошибки, ссылка, формула или функция. Тип аргумента должен соответствовать типу в описании функции. Если при задании формулы были допущены ошибки, результатом ее вычисления будет так называемое значение ошибки. Ошибка #####
|
||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1063; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.237.52 (0.017 с.) |

 ,
, 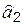 параметров
параметров  ,
,  оценки
оценки 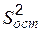 дисперсии
дисперсии  и оценки
и оценки 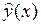 (эмпирической зависимости) неизвестной истинной зависимости
(эмпирической зависимости) неизвестной истинной зависимости 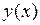 становится необоснованным, и правильнее исходить из предположения об их смещенности. Для того, чтобы проверить гипотезу о несмещенности модели (говорят об адекватности модели опытным данным), пользуются статистическими критериями.
становится необоснованным, и правильнее исходить из предположения об их смещенности. Для того, чтобы проверить гипотезу о несмещенности модели (говорят об адекватности модели опытным данным), пользуются статистическими критериями.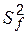 , где
, где 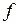 – число степеней свободы этой оценки:
– число степеней свободы этой оценки: . (6.9)
. (6.9) . (6.10)
. (6.10) . В нашем конкретном случае, когда модель имеет вид прямой линии, остаточная дисперсия (6.7) соответствует
. В нашем конкретном случае, когда модель имеет вид прямой линии, остаточная дисперсия (6.7) соответствует 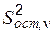 (числитель статистики). Для нахождения знаменателя следует перейти к более сложной модели, содержащей не 2, а 3 параметра (параболе второй степени), и найти для нее остаточную дисперсию. Однако этот вопрос выходит за рамки изучаемого курса, поэтому в данной работе предполагается, что имеется независимая несмещенная оценка дисперсии, либо известна сама дисперсия
(числитель статистики). Для нахождения знаменателя следует перейти к более сложной модели, содержащей не 2, а 3 параметра (параболе второй степени), и найти для нее остаточную дисперсию. Однако этот вопрос выходит за рамки изучаемого курса, поэтому в данной работе предполагается, что имеется независимая несмещенная оценка дисперсии, либо известна сама дисперсия  вычислить доверительные границы для истинного значения при данном значении аргумента, т.е. построить доверительный t-интервал для истинного значения при данном значении аргумента. Такие доверительные t-интервалы называются индивидуальными t-интервалами. Если повторять опыты (каждый раз с новыми опытными данными в тех же узлах) и следить за любым выбранным узлом, то доля индивидуальных t-интервалов, накрывающих истинное значение в этом узле (любом) будет в точности равна заданной доверительной вероятности. Однако, если мы будем следить за несколькими узлами (например, за всеми), то мы заметим, что доля узлов, в которых накрытие не имеет место в данном опыте, совсем не соответствует этой доверительной вероятности. Доля узлов, в которых накрытие не имеет места, может оказаться весьма значительной. От этого недостатка свободны так называемые совместные доверительные интервалы, которые обеспечивают одновременное накрытие истинных значений во всех узлах с вероятностью не меньше заданной.
вычислить доверительные границы для истинного значения при данном значении аргумента, т.е. построить доверительный t-интервал для истинного значения при данном значении аргумента. Такие доверительные t-интервалы называются индивидуальными t-интервалами. Если повторять опыты (каждый раз с новыми опытными данными в тех же узлах) и следить за любым выбранным узлом, то доля индивидуальных t-интервалов, накрывающих истинное значение в этом узле (любом) будет в точности равна заданной доверительной вероятности. Однако, если мы будем следить за несколькими узлами (например, за всеми), то мы заметим, что доля узлов, в которых накрытие не имеет место в данном опыте, совсем не соответствует этой доверительной вероятности. Доля узлов, в которых накрытие не имеет места, может оказаться весьма значительной. От этого недостатка свободны так называемые совместные доверительные интервалы, которые обеспечивают одновременное накрытие истинных значений во всех узлах с вероятностью не меньше заданной. , (6.11)
, (6.11) – критическое значение статистики f для выбранного уровня значимости
– критическое значение статистики f для выбранного уровня значимости 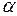 и с числами степеней свободы
и с числами степеней свободы  (числитель) и
(числитель) и 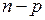 (знаменатель).
(знаменатель).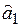 и
и 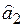 уравнения прямой регрессии (6.2); 2) воспользоваться встроенными функциями Microsoft Excel. Опишем оба подхода к решению задачи.
уравнения прямой регрессии (6.2); 2) воспользоваться встроенными функциями Microsoft Excel. Опишем оба подхода к решению задачи.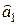 была равна 0.
была равна 0.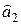 в строке формул запишем:
в строке формул запишем: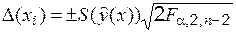 в точках
в точках 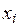 .
. Проверить гипотезу о независимости признаков, вычислить коэффициент связи
Проверить гипотезу о независимости признаков, вычислить коэффициент связи 
 , если группы и признаки разбиты на подгруппы и уровни. Мы ограничимся статистическим анализом таблицы сопряженности 2´2.Ознакомиться подробнее с таблицами сопряженности и их обработкой можно по [11].
, если группы и признаки разбиты на подгруппы и уровни. Мы ограничимся статистическим анализом таблицы сопряженности 2´2.Ознакомиться подробнее с таблицами сопряженности и их обработкой можно по [11]. Иначе можно записать так:
Иначе можно записать так: 
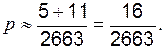 Соответственно, вероятность не заболеть приблизительно равна
Соответственно, вероятность не заболеть приблизительно равна 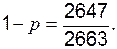 Таким образом, нам следует сравнить полученные в опыте частоты (
Таким образом, нам следует сравнить полученные в опыте частоты ( ) с теоретическими, вычисленными в предположении, что гипотеза
) с теоретическими, вычисленными в предположении, что гипотеза  справедлива. Это проще всего сделать с помощью известного из курса теории вероятностей и математической статистики критерия
справедлива. Это проще всего сделать с помощью известного из курса теории вероятностей и математической статистики критерия  . Отметим, что это приближенный критерий, существуют и другие, более точные критерии, но они более сложны. Составим новую таблицу, в которой наряду с наблюдаемыми частотами (верхнее число в каждой ячейке) укажем также ожидаемые в предположении справедливости нулевой гипотезы частоты, равные произведению общего числа наблюдений
. Отметим, что это приближенный критерий, существуют и другие, более точные критерии, но они более сложны. Составим новую таблицу, в которой наряду с наблюдаемыми частотами (верхнее число в каждой ячейке) укажем также ожидаемые в предположении справедливости нулевой гипотезы частоты, равные произведению общего числа наблюдений 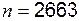 на соответствующие вероятности
на соответствующие вероятности 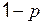 (они указаны во второй строке ячеек в круглых скобках).
(они указаны во второй строке ячеек в круглых скобках).  , (7.1)
, (7.1)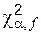 – верхний
– верхний  -предел статистики
-предел статистики  (7.2)
(7.2) ), т.е.
), т.е. 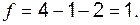 Обратите внимание на то, что разности между частотами в каждой ячейке равны по модулю, т.е. чтобы найти их нужно сделать лишь одно вычисление.
Обратите внимание на то, что разности между частотами в каждой ячейке равны по модулю, т.е. чтобы найти их нужно сделать лишь одно вычисление.
 :
: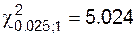 ;
;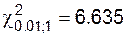 .
.
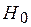 по формуле
по формуле 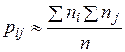 , где
, где 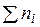 – сумма значений по строке;
– сумма значений по строке; 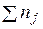 – сумма значений по столбцу;
– сумма значений по столбцу; 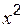 по формуле (7.1). При необходимости сформируйте вспомогательную таблицу значений выражения под знаком суммы.
по формуле (7.1). При необходимости сформируйте вспомогательную таблицу значений выражения под знаком суммы.

 Изменить формулу. По этому признаку Excel запускает Палитру формул, которая проверяет синтаксис, автоматически исправляет распространенные ошибки и обеспечивает справочными сведениями.
Изменить формулу. По этому признаку Excel запускает Палитру формул, которая проверяет синтаксис, автоматически исправляет распространенные ошибки и обеспечивает справочными сведениями. Ф ункция… либо одноименную кнопку на панели инструментов Стандартная. В результате будет запущен двухшаговый Мастер функций, содержащий всю коллекцию функций Excel в более чем 10 различных категорий.
Ф ункция… либо одноименную кнопку на панели инструментов Стандартная. В результате будет запущен двухшаговый Мастер функций, содержащий всю коллекцию функций Excel в более чем 10 различных категорий.


