
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Причины возникновения ошибкиСодержание книги
Поиск на нашем сайте
1. Использован оператор, задающий пересечение диапазонов, не имеющих общих ячеек. Меры по устранению ошибки – задайте правильно размерность пересекающихся диапазонов или не используйте оператор пересечения, если диапазоны не являются таковыми. В Microsoft Excel оператором пересечения диапазонов является пробел ().
ПРИЛОЖЕНИЕ 3 Кратка теория диаграмм Диаграммы являются средством визуального анализа данных. В любой современной системе программирования есть подобные графические Таблица 1 Технические характеристики Excel-диаграмм
Excel предоставляет пользователю 14 стандартных типов диаграмм: гистограмма, линейчатая, график, круговая, точечная, с областями, кольцевая, лепестковая, поверхность, пузырьковая, биржевая и другие. Каждый стандартный тип имеет несколько разновидностей. Постоянно наращивается палитра встроенных нестандартных типов. Коллекция типов диаграмм доступна из меню Диаграмма – Тип диаграммы. Инженерные приложения используют следующие типы диаграмм:
- точечный график строит график функции по точкам (x, y) без ограничений на вид функции. - сглаженные линии на Графике и Точечной диаграмме соединяют точки плавной кривой. - поверхность – это график трехмерной поверхности z (x, y). - контурная поверхность, проекция трехмерной поверхности на координатную плоскость XY в виде карты изолиний z (x, y) = Const. Организация данных в диаграммах описывается следующей терминологией. Диаграмма – графический объект на листе Excel. Активная диаграмма запускает в верхнем меню пункт Диаграмма, а также меню Вид и Формат настраиваются для работы с конкретной диаграммой. Продолжение прил. 3
Элементы диаграммы – отдельные объекты, составляющие диаграмму, довольно разнородные и отличаются для разных типов диаграмм. Элементы активной диаграммы собраны в список на панели инструментов Диаграммы. Все элементы диаграмм оснащены всплывающими подсказками. Область диаграммы – прямоугольная область, охватывающая все элементы диаграммы. Область построения на плоских диаграммах – это ограниченный координатными осями прямоугольник, содержащий ряды данных. На объемных диаграммах – охватывает три координатные оси со всеми подписями. Заголовок диаграммы – надпись с описательным текстом. По умолчанию располагается по центру над областью построения. Ряд данных – группа связанных данных диаграммы. Например, ряд данных для графика составляет диапазон значений функции. На одной диаграмме можно изобразить несколько рядов данных, каждый своим цветом. В качестве имен рядов данных Excel использует заголовки столбцов (или строк) диапазона данных. Если автоматическое распознавание имен рядов прошло безуспешно, Excel сгенерирует имена рядов по умолчанию: Ряд1, Ряд2, Ряд3,.. Имена рядов выводятся в легенду. Точка данных обозначается на диаграмме маркером – это точка, маркер, столбик, сегмент или другой графический примитив, например, на гистограмме это цветной столбик, на графике – квадратик в 5 пунктов. Легенда. Подпись с условными обозначениями цвета/закраски рядов данных. Легенда обычно располагается справа от области построения. Ключ легенды – условное обозначение в легенде слева от имени ряда, назначенное этому ряду. Категории – это значения независимой переменной, от которой зависят значения рядов данных, обычно откладываются на горизонтальной оси. Например, на графике значения категорий – это значения аргумента функции. Имена категорий используются для подписей делений оси категорий. Excel пытается распознать заголовки строк (или столбцов) данных для использования их в качестве имен категорий по отличающемуся форматированию первого столбца, иначе автоматически нумерует категории 1, 2, 3,.. В противном необходимо вручную указать адреса ячеек с именами категорий. Оси – это линии, используемые как основа измерений для построения данных на диаграмме. Ось категорий обычно отображается по горизонтальной оси, например, на графике соответствует оси X, оси независимой переменной. Ось значений – это обычно вертикальная ось, ось Y. Например, на графике значение точки данных изображает расстояние от маркера точки по вертикали до оси категорий в выбранных единицах измерения. Деления и подписи делений осей – это короткие насечки на оси через одинаковые расстояния, их подписи показывают откладываемую по оси меру, а также могут обозначать категории или ряды. Линии сетки – параллельные осям линии, облегчающие просмотр данных на диаграмме.
Окончание прил. 3
Подписи значений отображают дополнительные сведения: значения в отдельных точках, названия категорий, рядов или их комбинации. К элементам диаграмм также относятся заголовки осей, линии проекции, вспомогательные оси, линии рядов, тренды, коридоры колебания, полосы повышения и понижения, планки погрешности и другие. В табл. 2 приведены способы создания диаграммы в Excel. Рекомендуется использовать последний способ. Четырехшаговый мастер диаграмм выпытает у вас все параметры диаграммы и создаст с первого раза близкий к желаемому результат. Таблица 2 Способы создания диаграммы
Размещенная на отдельном листе книги или внедренная в текущий лист диаграмма связана с данными, на основе которых она создана, и обновляется автоматически при их изменении.
ПРИЛОЖЕНИЕ 4 Статистические таблицы Приведены краткие выдержки из таблиц математической статистики, необходимые и достаточные для выполнения упражнений, приведенных в сборнике. Более точные таблицы см. в [9]. Таблица 1 Интегральная функция нормированного нормального распределения
В первом столбце и в верхней строке указаны значения аргумента.
Продолжение прил. 4
Таблица 2 Дифференциальная функция нормированного нормального распределения (плотность вероятности)
Продолжение прил. 4
Таблица 3 Коэффициенты Стьюдента (двухсторонние границы t-распределения)
Таблица 4
Критические значения для наибольшего отклонения эмпирической Значения
Для
Продолжение прил. 4
Таблица 5 Распределение
Для построения двухстороннего интервала вероятности для случайной величины, имеющей
Верхнюю границу такого интервала находят по таблице для
Продолжение прил. 4 Таблица 6 Значения
Значения
Окончание прил. 4
Полезные соотношения:
где
СПИСОК ЛИТЕРАТУРЫ 1. Макарова Н.В. Статистика в Excel: Учебное пособие/ Макарова Н.В., Трофимец В.Я. – М.: Финансы и статистика, 2002. – 368 с. 2. Селиванов М. Н. Качество измерений / Селиванов М.Н., Фридман А.Э., Кудряшева Т.Ф. – Л.: Лениздат, 1987. 3. Новицкий П. В. Оценка погрешностей результатов измерений / Новицкий П.В., Зограф И.А. – Л.: Энергоатомиздат, 1985. 4. Гмурман В.Е. Теория вероятностей и математическая статистика/ Гмурман В.Е. – М.: Высшая школа, 1997. 5. Чашкин Ю.Р. Статистика для инженеров. Основы регрессионного анализа/ Чашкин Ю.Р. – Хабаровск: Изд-во ДВГУПС, 2003. – 162 с. 6. Худсон Д. Статистика для физиков / Худсон Д. – М.: Мир, 1970. 7. Гмурман В.Е. Руководство к решению задач по теории вероятностей и математической статистике: Учеб. Пособие для студентов вузов. Изд. 5-е, стер/ Гмурман В.Е. – М.: Высш. шк., 1999. 8. Чашкин Ю.Р. Математическая статистика. Статистическая обработка результатов измерений. Уч.-метод. пособие для самостоят. работ студентов / Чашкин Ю.Р. – Хабаровск: Изд-во ДВГУПС, 1999. 9. Большев Л.Н. Таблицы математической статистики / Большев Л.Н., Смирнов Н.В. – М.: Наука, 1983. 10. Тюрин Ю.Н. Статистический анализ данных на компьютере / Тюрин Ю.Н., Макаров А.А. Под ред. В.Э.Фигурнова – М.: ИНФРА-М, 1998. 11. Справочник по прикладной статистике. – В 2-ч т. – Т.1: Пер. с англ. / Под ред. Э. Ллойда, У.Ледермана, Ю.Н.Тюрина. – М.: Финансы и статистика, 1989. –370с. 12. Себер Дж. Линейный регрессионный анализ / Себер Дж. – М.: Мир, 1980. 13. Вучков И. Прикладной линейный регрессионный анализ / Вучков И., Бояджиева Л., Солаков Е. –М.: Финансы и статистика, 1987. 14. Дрейдер Н. Прикладной регрессионный анализ. В 2-х кн. Пер. с англ. – 2-е изд., перераб.и доп. / Дрейдер Н., Смит Г. – М.: Финансы и статистика, 1987. 15. Вихтенко Э. М. Численные методы на ЭВМ/ Вихтенко Э.М., Коломийцева С.В., Комова О.С. – Хабаровск: ДВГУПС, 2003. –71с.
ОГЛАВЛЕНИЕ
ВВЕДЕНИЕ............................................................................................................ 1 ЛАБОРАТОРНАЯ РАБОТА № 1 ПЕРВИЧНАЯ ОБРАБОТКА РЕЗУЛЬТАТОВ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /вычисление основных статистических параметров/............................................................................. 2 1. Цель работы................................................................................................ 2 2. Задание........................................................................................................ 2 3. Краткая теория........................................................................................... 2 4. Ход работы.................................................................................................. 5 5. Контрольные вопросы............................................................................ 10 ЛАБОРАТОРНАЯ РАБОТА № 2 ПОСТРОЕНИЕ ГИСТОГРАММЫ ПО РЕЗУЛЬТАТАМ ПРЯМЫХ МНОГОКРАТНЫХ ИЗМЕРЕНИЙ /на примере результатов математического эксперимента/............................................. 11 1. Цель работы............................................................................................. 11 2. Задание..................................................................................................... 11 3. Краткая теория......................................................................................... 11 4. Ход работы................................................................................................ 15 5. Контрольные вопросы............................................................................ 18 ЛАБОРАТОРНАЯ РАБОТА № 3 ПРОВЕРКА НОРМАЛЬНОСТИ ЗАКОНА РАСПРЕДЕЛЕНИЯ /тремя различными методами/................................... 18 1. Цель работы............................................................................................. 18 2. Задание..................................................................................................... 18 3. Краткая теория......................................................................................... 19 4. Ход работы................................................................................................ 23 5. Контрольные вопросы............................................................................ 26 ЛАБОРАТОРНАЯ РАБОТА № 4 ОБЪЕДИНЕНИЕ РАВНОТОЧНЫХ СЕРИЙ ИЗМЕРЕНИЙ /двухвыборочный t-тест для средних/.................................. 27 1. Цель работы............................................................................................. 27 2. Задание..................................................................................................... 27 3. Краткая теория......................................................................................... 27 4. Ход работы................................................................................................ 29 5. Контрольные вопросы............................................................................ 35 ЛАБОРАТОРНАЯ РАБОТА № 5 ОБЪЕДИНЕНИЕ СЕРИЙ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ /двухвыборочный t-тест для средних/................................. 36 1. Цель работы............................................................................................. 36 2. Задание..................................................................................................... 36 3. Краткая теория......................................................................................... 36 4. Ход работы................................................................................................ 38 5. Контрольные вопросы............................................................................ 41 ЛАБОРАТОРНАЯ РАБОТА № 6 ПОСТРОЕНИЕ ЛИНЕЙНОЙ ЭМПИРИЧЕСКОЙ ЗАВИСИМОСТИ ПО ОПЫТНЫМ ДАННЫМ /метод наименьших квадратов/ 41 1. Цель работы............................................................................................. 41 2. Задание..................................................................................................... 41 3. Краткая теория......................................................................................... 42 4. Ход работы................................................................................................ 46 5. Контрольные вопросы............................................................................ 49 ЛАБОРАТОРНАЯ РАБОТА № 7 ОЦЕНКА СВЯЗИ НОМИНАЛЬНЫХ ПРИЗНАКОВ /таблицы сопряженности/................................................................................ 49 1. Цель работы............................................................................................. 49 2. Задание..................................................................................................... 49 3. Краткая теория......................................................................................... 49 4. Ход работы................................................................................................ 52 5. Контрольные вопросы............................................................................ 52 ЗАКЛЮЧЕНИЕ.................................................................................................... 53 ПРИЛОЖЕНИЕ 1.................................................................................... 54 Установка надстройки "Пакет анализа".......................................... 54 ПРИЛОЖЕНИЕ 2.................................................................................... 56 Виды ошибок при задании формул.................................................. 56 ПРИЛОЖЕНИЕ 3.................................................................................... 61 Кратка теория диаграмм..................................................................... 61 ПРИЛОЖЕНИЕ 4.................................................................................... 64 Статистические таблицы.................................................................... 64 СПИСОК ЛИТЕРАТУРЫ................................................................................... 70
[1] Несмотря на широкое распространение, нормальное распределение не универсально. Если нет уверенности в его применимости, следует проверить возможность использования нормального распределения для описания случайной величины с помощью критериев согласия (см. лаб. работу «Проверка нормальности закона распределения»). [2] Это определение является строгим лишь для распределений экспоненциального типа, например, нормального. В этом случае существует так называемая «граница Крамера-Рао» как минимально возможная дисперсия оценки. Оценка, дисперсия которой достигает этой границы, называется эффективной. Для распределений с плотностью вероятности, имеющей точки разрыва 1-го или 2-го рода (равномерного, арксинусного, двойного экспоненциального и др.) могут быть построены сверхэффективные оценки (их дисперсия существенно меньше дисперсии среднего арифметического). [3] Одинаковые значения в вариационном ряде должны повторяться столько раз, сколько они встречаются в выборке. [4] Функция ОКРУГЛВВЕРХ округляет число по модулю до ближайшего большего целого. Вторым аргументом является количество цифр, до которого округляется число. Замечание: Если количество цифр больше 0 (нуля), то число округляется с избытком до заданного количества десятичных разрядов после десятичной запятой. Если количество цифр равно 0 или опущено, то число округляется с избытком до ближайшего целого. Если количество цифр меньше 0, то число округляется с избытком, с учетом десятичных разрядов слева от десятичной запятой. [5] Теоретическая кривая nPj рассчитывается по результатам лаб.раб. №3 «Проверка нормальности…» с помощью критерия согласия. В данной работе может служить огибающей гистограммы. Приводится для наглядности. [6] Отметим, что вопрос о минимальном числе значений в интервале не имеет строгого решения. Автор критерия К.Пирсон считает, что не должно быть пустых интервалов [8]. Мы можем порекомендовать следующий выход из положения: примем. Если при вычислении статистики критерия одно из слагаемых окажется существенно больше остальных, причем будет мало (< 5), объедините этот интервал с соседним. [7] Нужно отметить, что границ интервалов на одно значение больше чем частот, [8] функция ФТЕСТ рассчитывает двустороннее -значение F-теста, поэтому для рассматриваемого случая это значение делится на 2. [9] Если то -значение F-теста рассчитывается с помощью функции FРАСП, вычтенной из 1. [10] С
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 263; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.177.252 (0.012 с.) |

 - график отображает значения однозначной функции y (х) с равными промежутками по аргументу x.
- график отображает значения однозначной функции y (х) с равными промежутками по аргументу x.




 ;
;  ;
; 
 ;
;  ;
; 




 , удовлетворяющие условию
, удовлетворяющие условию 

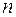
 используют аппроксимации:
используют аппроксимации:
 .
. (процентные точки).
(процентные точки).  , удовлетворяющие условию
, удовлетворяющие условию 

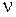

 ‑распределение, удовлетворяющего условию
‑распределение, удовлетворяющего условию  , следует учесть, что
, следует учесть, что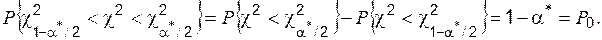
 , а нижнюю – для
, а нижнюю – для  .
. для
для 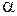 = 0.05 (верхние 5‑процентные
= 0.05 (верхние 5‑процентные 

 для
для  = 0.10 (верхние 10‑процентные
= 0.10 (верхние 10‑процентные 
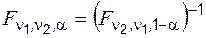 ;
;  ,
, –
–  -процентная точка t-распределения, соответствующая вероятности
-процентная точка t-распределения, соответствующая вероятности  или коэффициент Стьюдента (двухсторонняя граница t-распределения, табл. 3).
или коэффициент Стьюдента (двухсторонняя граница t-распределения, табл. 3).


