
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Кинематика и динамика подъёмных систем с органами навивки переменного радиусаСодержание книги
Поиск на нашем сайте
Кинематика подъемных систем На рис. 49, а, б, показана диаграмма изменения угловой скорости Угловая скорость w измеряется в радианах в секунду (рад/с), причем один радиан равняется 180/π. Между частотой вращения nб органа навивки и угловой скоростью w существует зависимость
Угловое ускорение (замедление) ε (рад/с2) зависит от ω и продолжительности ускоренного t (замедленного) вращения:
Вся площадь диаграммы угловой скорости представляет собой угол поворота органа навивки за время одной подъемной операции. Отдельные элементы всей площади диаграммы угловой скорости являются углами поворота (рад) органа навивки в различные периоды вращения: за время t1 равномерно ускоренного обращения
за время t2 равномерного вращения
эа время
Полный угол поворота (рад) органов навивки канатов за время Т движения подъемных сосудов Ф = Ф1 + Ф2 + Ф3 (117)
Рис. 49 - Диаграммы подъемной системы с органами навивки переменного радиуса: А - угловой скорости органа навивки, б - углового ускорения, в - изменения радиусов навивки поднимающейся и опускающейся областей каната, г и д – скорости и ускорения поднимающейся ветви, е и ж – скорости и ускорения опускающейся ветви.
Подставляя значения Ф1,Ф2,Ф3 у выражения (117), аналогично выводу формулы (49) получим расчетную максимальную угловую скорость вращения (рад/с) органов навивки:
где εг — модуль угловых ускорений (рад/с2)
При определении ωрм заданными величинами являются Тр и Ф. Значениями ε1 и ε3 задаются из условия допускаемых по ПТЭ значений линейных ускорения и замедления. По данным выбранной машины определяют фактическую максимальную угловую скорость ωmax, причём для обеспечения заданной производительности подъемной установки ωmax ≥ ωр.г. Продолжительности (с) ускоренного и замедленного обращения органов навивки соответственно равные:
Углы Ф1 и Ф3, поворота органов навивки за указанное время определяют по формулам (114) и (116), причем в числителе этих выражений необходимо поставить ωmax.
Угол поворота и продолжительность равномерного вращение органов навивки:
Пути, пройденные подъемные сосудом за период поворота органа навивки на определенный угол, получают умножением углов поворота органов навивки на полусумму соответствующих начальному и конечному углам поворота радиусов навивки. Линейные скорости, линейные ускорения и пути за различные периоды диаграммы скорости будут отличными для поднимающегося и опускающегося подъемных сосудов, так как радиусы навивки канатов поднимающейся и опускающейся ветвей переменны и отличаются друг от друга. Для перевода угловой скорости ω и углового ускорения ε вращения органов навивки соответственно в линейную скорость υ (м/с) и линейное ускорение а (м/с2) движения подъемных сосудов имеем: υx = ωxRx (124) ax = εxRx (125) где Rx — радиус навивки каната, соответствующий значению скорости ω или ускорению εx; Точнее линейное ускорение ax =εxRx + Во время t равномерного вращения органа навивки с некоторой скоростью ω, но при увеличении радиуса навивки от Rн к Rк подъемный сосуд будет двигаться с ускорением, а при уменьшении радиуса навивки подъемный сосуд будет двигаться с замедлением, обусловленным по формуле
Рассчитав элементы диаграммы угловой скорости и углового ускорения вращение органов навивки и определив в ее характерных точках значения радиусов поднимающейся и опускающейся ветвей, по формулам (122) — (124) находят соответственно значения скоростей и ускорений поднимающегося и опускающегося подъемных сосудов, что дает возможность построить диаграммы линейных скоростей и ускорений за время одной подъемной операции. Характер этих диаграмм, таким образом, будет определятся указанными выше диаграммами w и ε и законом изменения радиуса навивки каната. Пути, пройденные подъемными сосудами, можно определить, как величину соответствующих площадок диаграмм линейных скоростей. На рис 49 показанные диаграммы линейной скорости и линейного ускорения для поднимающегося и опускающегося подъемных сосудов при трехпериодной диаграмме угловой скорости вращения конических барабанов.
При подъемных системах с неопрокидными скипами применяют пятипериодную или четырехпериодную диаграмму угловой скорости, а при опрокидных сосудах — семипериодную или шестипериодную диаграмму. Значение линейных скоростей, ускорений и замедлений при движении ролика подъемных сосудов по разгрузочным кривым. Динамика подъемной машины Основное динамическое уравнение подъемной установки с органами навивки переменного радиуса на основании формулы (79) имеет вид (Н·м)
В выражении (127) для удобства расчетов динамический момент подъемной системы представлен суммой динамического момента МД.ВР вращающихся частей, который зависит от углового ускорения е, и динамических моментов поступательно движущихся частей поднимающейся Мд.п и опускающейся МД.О ветвей, зависящих от линейного ускорения a каждой из ветвей. Статический момент (Н·м) подъемной системы представляет собой разность статических моментов поднимающейся и опускающейся ветвей каната (рис. 50):
где g hXП hXO — путь, пройденный соответственно поднимающимся и опускающимся подъемным сосудом от начала подъемной операции, м; RП и RO — радиусы навивки соответственно поднимающейся и опускающейся ветви каната, м.
Динамический момент вращающихся частей
где Динамический момент поднимающейся ветви каната
Динамический момент опускающейся ветви каната
где а0 — линейное ускорение опускающейся ветви каната, м/с2. Моменты инерции (кг·м8) частей подъемной системы: 1) органов навивки — в зависимости от конструкции принимается по данным заводов; 2) витков каната определяется по формулам; для каната, навитого на цилиндрическую часть органов навивки,
для каната, навитого на коническую часть органов навивки, приближенно
где p - линейная масса подъемного каната, кг/м; 3) ротора
где Ориентировочную мощность подъемного двигателя находят по формуле (90). Значение коэффициента динамического режима р принимают по данным, приведенным в § 51. На основании формулы (127) определяют вращающий момент подъемного двигателя в характерных точках диаграммы скорости и строят нагрузочную диаграмму на двигатель, т. е. диаграмму вращающего момента за время одной подъемной операции. Мощность (кВт) на валу подъемного двигателя в любой момент подъемной операции
где
На основании формулы (136) определяют мощность на валу подъемного двигателя в характерных точках диаграммы угловой скорости и строят диаграмму мощности за время одной подъемной операции.
4.11.3 Особенности кинематики и динамики
1) период ускоренного вращения барабана до максимальной угловой скорости ωmax c угловым ускорением ε1, когда поднимающаяся ветвь каната движется с линейным ускорением аП1 =ε1RМ.Ц - а опускающаяся - с ускорением ао1 = ε1Rб.Ц, где RМ.Ц и Rб.Ц — радиусы соответственно малого и большого, цилиндров. В этот период все движущиеся элементы установки создают динамическую нагрузку на двигатель. При асинхронном двигателе для уменьшения потерь в реостате этот период должен быть по возможности коротким, но в пределах, соответствующих допускаемой перегрузке двигателя; 2) период вращения барабана с ωmax, когда поднимающаяся ветвь каната, навиваясь на конус барабана, движется с ускорение
где tкс — время навивки каната на конус. При этом динамическая нагрузка создается только поднимающейся ветвью каната (подъемный сосуд, канат, направляющий шкив), остальные элементы установки движутся с равномерной скоростью; 3) период движения, когда барабан вращается с ωmax, поднимающаяся и опускающаяся ветви каната, соответственно навиваясь и свиваясь с большого цилиндра, движутся с равномерной скоростью. Динамическая нагрузка на двигатель в этот период не создается; 4) период вращения барабана с ωmax, когда поднимающаяся ветвь каната, навиваясь на большой цилиндр, продолжает двигаться с равномерной линейной скоростью, а опускающаяся ветвь, свиваясь с конуса, движется с замедлением
вследствие чего возникает отрицательная динамическая нагрузка, создаваемая опускающейся ветвью (подъемный сосуд, канат, направляющий шкив); 5) период замедленного вращения барабана до полной остановки с угловым замедлением ε3, когда поднимающаяся ветвь каната движется с линейным замедлением
При подъемной системе с опрокидными сосудами в расчете нагрузочных диаграмм должно быть учтено нарушение уравновешивания собственных масс сосудов в начале и конце подъемной операции, когда кузов опрокидного сосуда опирается на разгрузочные кривые. Статический момент (Н м) в начале движения подъемных сосудов
где kР = 0,65 - коэффициент, показывающий, какая часть собственной массы сосуда, находящегося на разгрузочных кривых, действует на канаты в начале подъемной операции. В конце движения подъемных сосудов
|
|||||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 1156; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.17.39.107 (0.009 с.) |

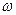 и углового ускорения ε вращение органа навивки при клетевом подъеме в функции времени t. Органы навивки вращаются с угловым ускорением ε1, затем равномерно с максимальной угловой скоростью wmax и наконец, с угловым замедлением ε3.
и углового ускорения ε вращение органа навивки при клетевом подъеме в функции времени t. Органы навивки вращаются с угловым ускорением ε1, затем равномерно с максимальной угловой скоростью wmax и наконец, с угловым замедлением ε3.
 (112)
(112) (113)
(113)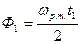 (114)
(114) (115)
(115) , равномерно замедленного вращения
, равномерно замедленного вращения (116)
(116)
 (118)
(118) (119)
(119) (120)
(120) (121)
(121) (122)
(122) ; (123)
; (123) , но из-за маленького значения величиной dR/dt пренебрегаем.
, но из-за маленького значения величиной dR/dt пренебрегаем. (126)
(126)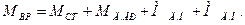 (127)
(127) (128)
(128) - сопротивление движению одного подъемного сосуда и его ветви каната, Н;
- сопротивление движению одного подъемного сосуда и его ветви каната, Н;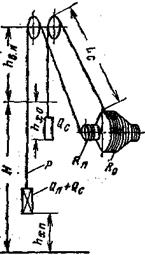 Динамический момент (Н·м) подъемной системы
Динамический момент (Н·м) подъемной системы (129)
(129) (130)
(130) ,
,  и
и  — моменты инерции находящихся на органах навивки витков каната соответственно поднимающейся и опускающейся ветвей и самого органа навивки, кг·м2;
— моменты инерции находящихся на органах навивки витков каната соответственно поднимающейся и опускающейся ветвей и самого органа навивки, кг·м2; 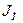 и
и  — моменты инерции зубчатых колес редуктора и ротора, приведенные к валу органов навивки, кг·м2.
— моменты инерции зубчатых колес редуктора и ротора, приведенные к валу органов навивки, кг·м2. (131)
(131)
 - расстояние от верхней приемной площадки до оси копрового шкива;
- расстояние от верхней приемной площадки до оси копрового шкива; - длина струны каната, м;
- длина струны каната, м;  - линейное ускорение поднимающейся ветви каната, м/с2
- линейное ускорение поднимающейся ветви каната, м/с2 (132)
(132) (133)
(133) (134)
(134) и
и  — длина каната, навитого соответственно на цилиндрическую и коническую части органов навивки, м;
— длина каната, навитого соответственно на цилиндрическую и коническую части органов навивки, м; 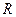 — радиус навивки каната на цилиндрическую часть барабана, м;
— радиус навивки каната на цилиндрическую часть барабана, м;  (135)
(135) — маховой момент ротора двигателя, Н·м2;
— маховой момент ротора двигателя, Н·м2;  - передаточное число редуктора.
- передаточное число редуктора.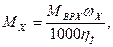 (136)
(136) — вращающий момент подъемного двигателя относительно оси вращения органов навивки и соответствующий угловой cкорости
— вращающий момент подъемного двигателя относительно оси вращения органов навивки и соответствующий угловой cкорости  ,
,  — к. п. д. передачи; при отрицательном моменте
— к. п. д. передачи; при отрицательном моменте 
 Диаграммы кинематики и динамики клетевой подъемной системы с бицилиндроконическими барабанами, построенные в соответствии с указаниями § 53 и 54, показаны на рис. 51. Если при органах навивки постоянного радиуса и клетевом подъеме для нагрузочных диаграмм с точки зрения динамики характерны три периода диаграммы скорости, то при установке с бицилиндроконическим барабаном для тех же условии их пять (см. рис. 51);
Диаграммы кинематики и динамики клетевой подъемной системы с бицилиндроконическими барабанами, построенные в соответствии с указаниями § 53 и 54, показаны на рис. 51. Если при органах навивки постоянного радиуса и клетевом подъеме для нагрузочных диаграмм с точки зрения динамики характерны три периода диаграммы скорости, то при установке с бицилиндроконическим барабаном для тех же условии их пять (см. рис. 51); (137)
(137) (138)
(138)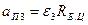 ,а опускающаяся – c замедлением
,а опускающаяся – c замедлением  . В этот период создается отрицательная динамическая нагрузка всеми движущимися элементами подъемной установки.
. В этот период создается отрицательная динамическая нагрузка всеми движущимися элементами подъемной установки.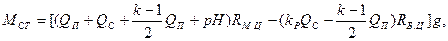 (139)
(139) (140)
(140)


