Умножение двоичных чисел машинным методом.

 

Умножение двоичных чисел машинным методом производится по следующим алгоритму:

1. Определяют знак произведения путём сложения по модулю два знаковых разрядов множителей.

2. Перемножение модулей чисел начиная с младшего разряда множителя одним из следующих способов умножения: 1)Множимое неподвижно сумматор частичных произведений сдвигается вправо. 2)Сумматор частичных произведений неподвижен множимое сдвигается влево.

Оба способа дают одинаковый результат, в обоих случаях умножение начинается с анализа младшего разряда множителя. Умножение производится в прямом коде.

1) Способ анализируется очередной разряд множителя: Если он равен 1 то к содержимому сумматора прибавляется множимое и сумматор сдвигается вправо. Если он равен 0 то производится только сдвиг сумматора вправо. Причём количество сдвигов равно количеству разрядов множителя, а количество прибавлений множимого к сумматору равно количеству единиц во множителе.

2) Анализируется второй разряд множителя если он равен единицы то множимое прибавляется в сумме частичных произведений и множимое сдвигается в лево на один разряд. Если он равен 0 то производится только сдвиг множимого влево.

 

 

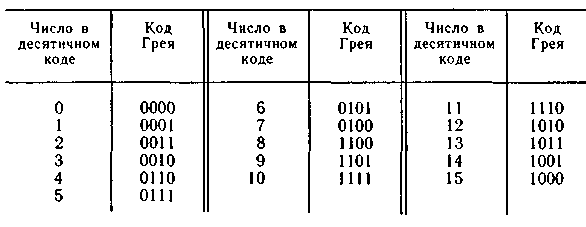
Особенно важным среди циклических является код Грэя. Он строится на базе двоичного по следующему правилу: старший разряд остаётся без изменения; каждый последующий разряд инвертируется если предыдущий разряд исходного двоичного кода равен единице.

 

Код Грея:

 

При использовании кода 4221 каждая цифра записывается в виде 4-х разрядной группы. Но её разряды начиная с левого представляют величины 4221. (д.з. сделать таблицу с кодом Грея от 0 до 15 и таблицу с кодами с остатком 3 и 4221 от 0 до 9).

 

 

Коды с выявлением ошибок

Общие сведения о кодах с выявлением ошибок

 

Одним из важнейших аспектов организации хранения и передачи кодов данных является обеспечение их надёжности и без ошибочности применяя специальные методы кодирования можно обеспечить контроль за появлением ошибки и даже восстановление исходного кода после её обнаружения. Применение этих методов позволяет снизить вероятность появления ошибки до 10^-9 и ниже. Общим методом обеспечения надёжности хранения и передачи данных в компьютере и по линиям связи является включение в код дополнительных контрольных разрядов. Существует много различных вариантов этого метода, рассмотрим код с проверкой чётности. При формировании кода слова в контрольный (дополнительный разряд) записывается 0 или 1 таким образом, что бы сумма единиц в слове, включая контрольный разряд, была чётной.

Пример (контроль по чётности 3-х разрядных слов):

В дальнейшем при всех передачах, слово передаётся вместе со своим контрольным разрядом. Если при передаче информации приёмное устройство обнаруживает, что в принятом слове значение контрольного разряда не соответствует чётности суммы единиц слова, то это воспринимается как признак ошибки. Код контроля по чётности обнаруживает все одиночные ошибки и все случаи не чётного числа ошибок. При одновременном возникновении двух или любого чётного числа ошибок, код с проверкой чётности не обнаруживает ошибок.

 

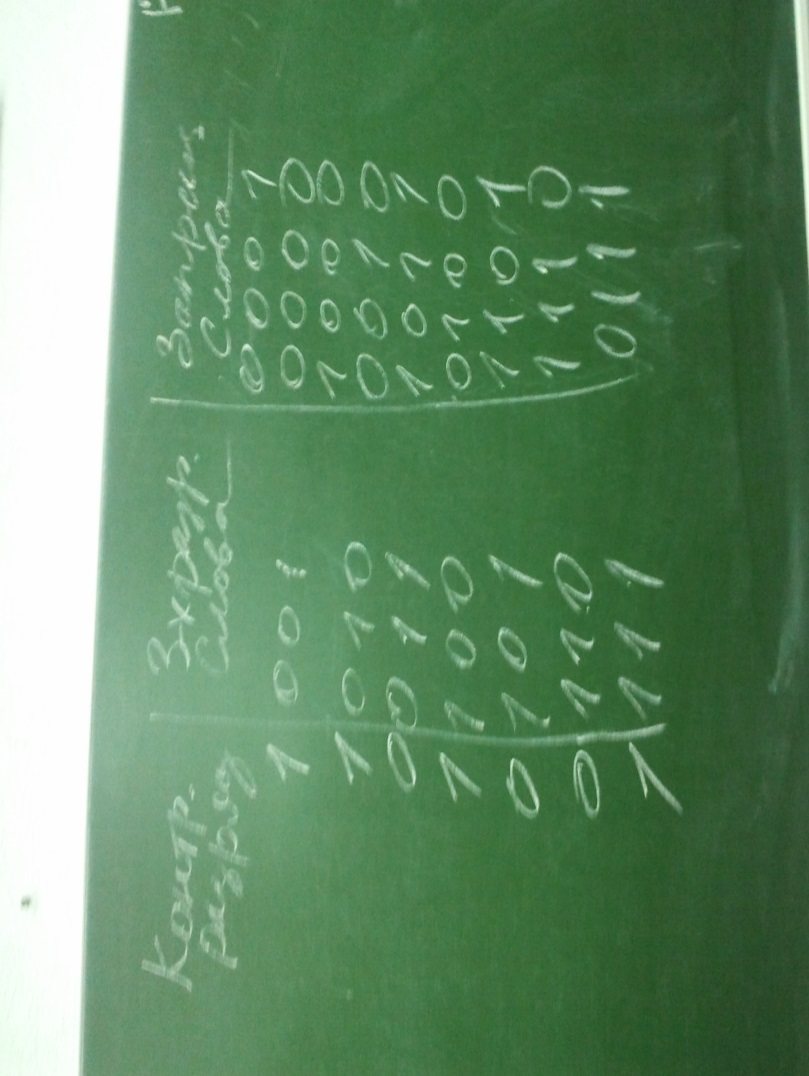
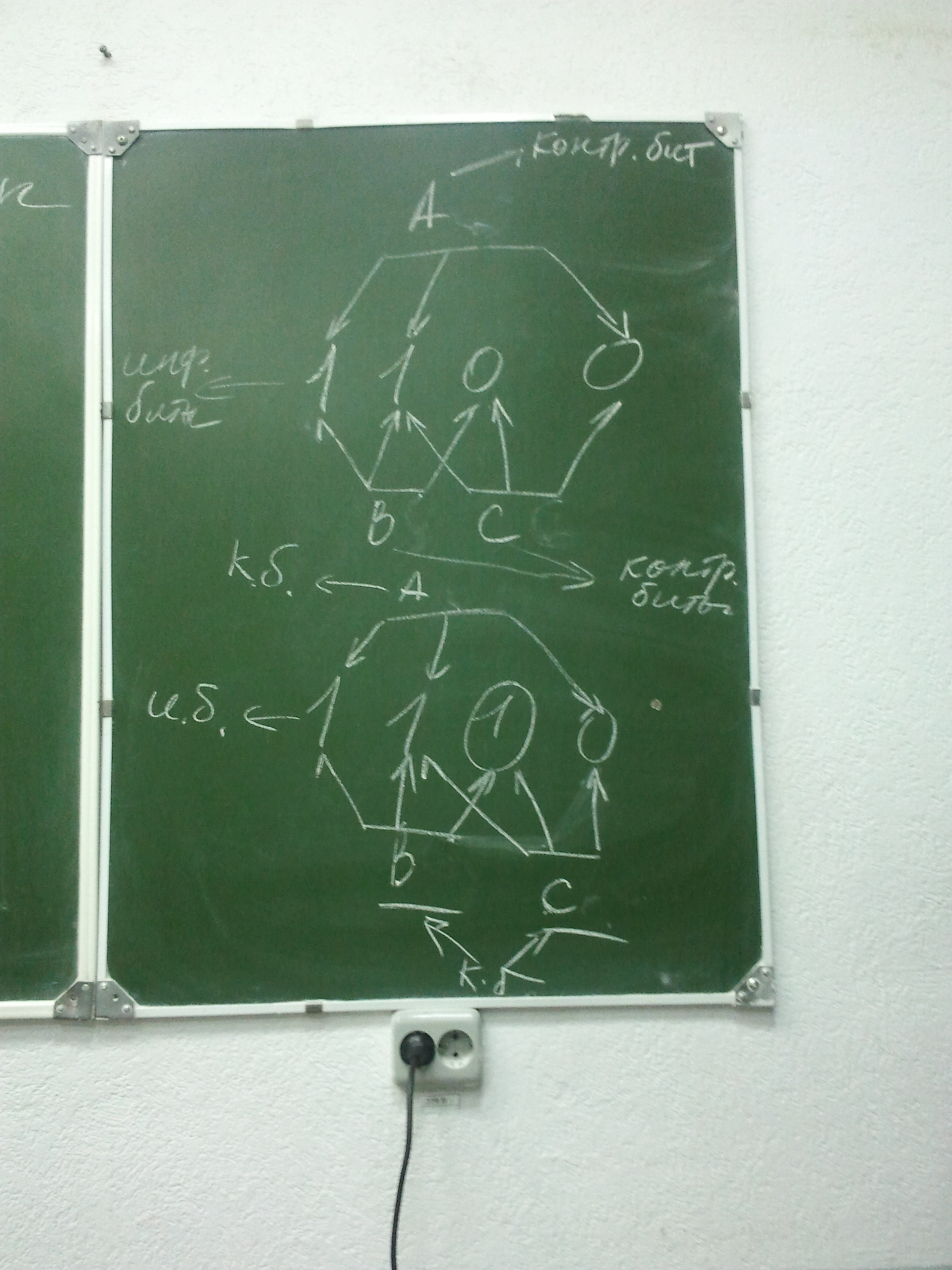
Существуют более развитые способы кодирования, которые не только позволяют установить факт появления ошибок большой кратности, но и обеспечивают их исправление. К таким способам относятся коды, принцип построения которых предложил Р. Хемминг.

Рассмотрим общую идею построения кодов Хемминга на следующем примере:

Пусть имеется исходный, 4-х битный код:

Чтобы не только обнаружить, но и исправить вероятную одиночную ошибку, предлагается каждую тройку битов снабдить одним контрольным разрядом (можно ограничится тремя тройками) количество единиц в каждой группе (тройка битов вместе с контрольным разрядом) должно быть не чётным. На рисунке изображены: исходный код и значения контрольных битов A B C. В каждой выбранной тройке.

Если во время выполнения действий один из битов окажется искажённым, то во всех группах в которые входит ошибочный бит, контроль не чётности покажет наличие ошибки. Следовательно, для определения положения ошибочного вида в коде достаточно выбрать разряд входящий во все группы в которых нарушена не чётность (на рисунке эти биты подчёркнуты). Ошибочный бит должен принадлежать одновременно двум группам. После обнаружения сбойного бита исправление кода осуществляется его инвертирование.

 

 

Алгебра логики и теоретические основы синтеза цифровых устройств

 

Тема 2.1: Элементы математической логики

 

Понятие алгебры-логики. Основные логические операции и логические элементы

 

 

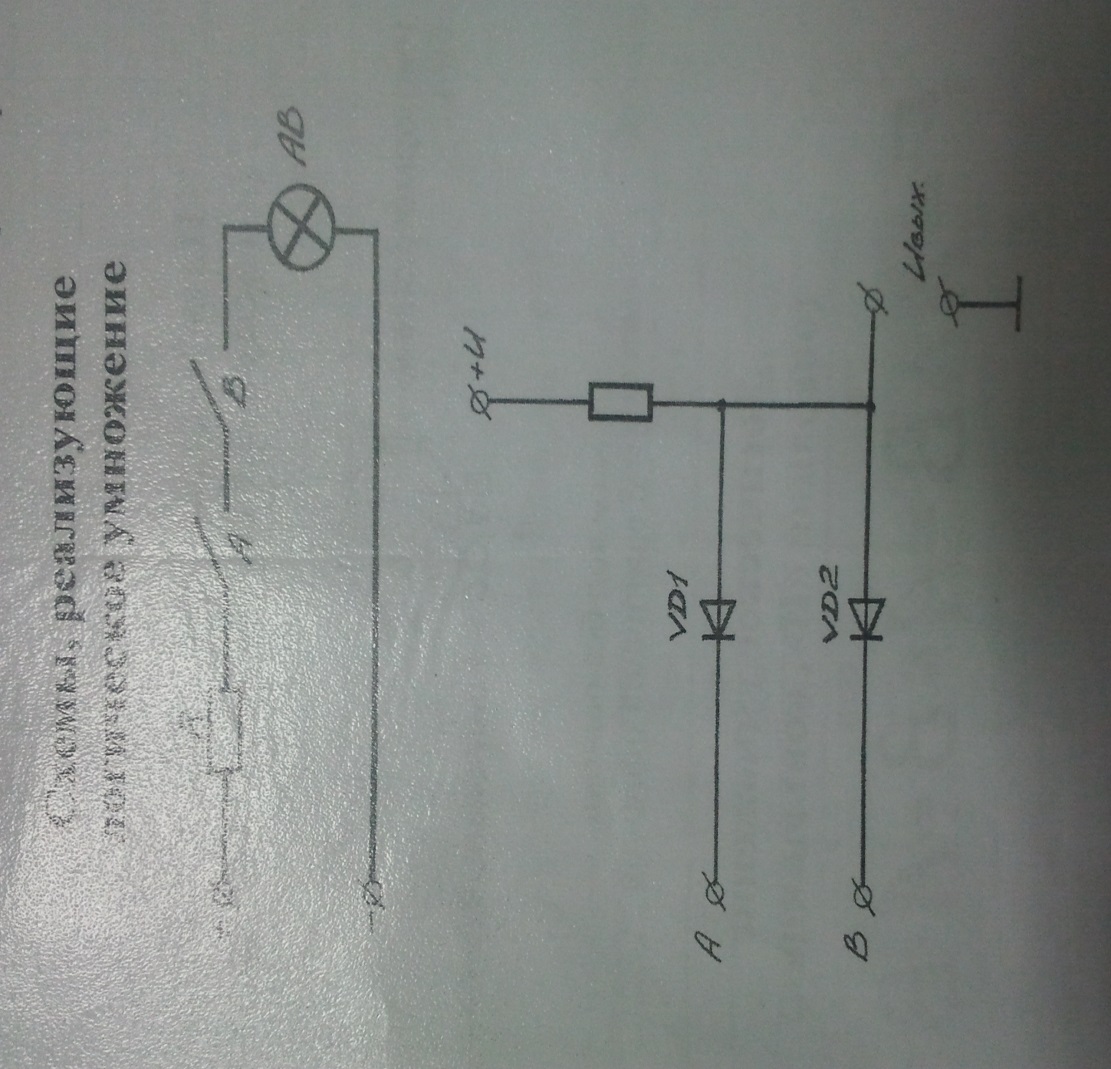
Для математического описания работы вычислительных устройств, синтеза и анализа схем (синтез – процесс создания устройства; анализ – упрощение устройства) используется алгебра логики (Белева алгебра). Область алгебры-логики состоит из множества высказываний обозначается A B C…X,Y.

Высказывание – законченное предложение, которое может иметь два значения истинности: либо быть истинным (А – истинно: А=1) либо быть ложным (С – ложно: С=0).

Высказывания могут быть истинными или ложными: первое не зависит от высказываний, а второе образуется из двух и более простых высказываний. Простое высказывание называют логическим переменным, а сложное логической функцией этих переменных переключательный функции (ПФ)

Операции алгебр логики:

1. Логическое умножение (операция «И», конъюнкция)

F=A^B=A&D=A*B=AB

Схема реализующая эту логическую операцию, называется схемой «И»

На выходе схемы «И» сигнал соответствует логической единице, тогда и только тогда, когда на всех входах одновременно будет сигнал логической единицы. Разрешающим уровнем схемы и является уровень логической единицы схемы «И», логическая функция от «н» переменной будет иметь 2ⁿ строк.

Схемы, реализующие логическое умножение:

На выходе схемы «ИЛИ» всегда соответствует логическому нулю, тогда и только тогда, когда на всех входах одновременно будет сигнал логического нуля. Разрешающим для схемы «ИЛИ» является уровень логического нуля.

 

Сложение по модулю 2

(Операция «исключающее ИЛИ», неравнозначность)

 

F=A+B

F=ABvAB

 

А	В	А+В	-А+В

 

 

 

Основные законы логики

 

 

AvI=1

A=0 A=1

0v1=1 1v1=1

Av-A=1

0v1=1 1v0=1

 

Тема 2.2: Формы логических функций и их использование для синтеза логических схем.

 

Формы логических функций:

F=A—C BvAC 1BvAC BA= ABC v A-BC vAB-C= ACvAB= --ACvAB= -AC*-AB

ПФ – могут быть выражены различными логическими формулами, благодаря возможности проведения над ними эквивалентных преобразований. На практике наиболее удобными для представления ПФ оказываются дизъюнктивные и конъюнктивные формы.

Эти формы представляют собой дизъюнкции элементарных конъюнкций или конъюнкций элементарных дизъюнкций.

Конъюнкция(дизъюнкция) любого числа называется элементарной если со множетялями(слагаемыми) в ней являются одиночные аргументы, либо описание одиночных аргументов.

Дизъюнктивной, нормальной формой(ДНФ), ПФ называется дизъюнкция любого числа элементарных конъюнкций, например:

Ранг элементарной конъюнкции(дизъюнкции) определяется числом переменных входящих в эту конъюнкцию(дизъюнкцию).

Совершенной ДНФ(СДНФ) ПФ имеющее n аргументов называется такая форма в которой все конъюнкции имеют ранг n:

 

ПФ может быть задана словестно, в виде таблицы истинности логического выражения. По словестному описанию составляют таблицу истинности, а затем записывают СДНФ в ПФ.

СДНФ, ПФ записывается по таблице истинности в следующей Последовательности:

1. Из таблицы истинности выделяются строки, в которых функция принимает значение единицы.

2. Записываются составляющие формулы в виде конъюнкции переменных или их отрицания. Если переменная в данном наборе = 1, то она входит в формулу как не отрицательная.

3. Конъюнкции определяют знаком дизъюнкции.

Пример:

Записать ПФ устройство функционирующего по следующему правилу: Сигнал на выходе схемы = 1, если хотя бы на двух входах из трёх отсутствует уровень логической единицы.

A	B	C	F

Конъюнктивные формы представления ПФ используются реже, чем дизъюнктивные. Конъюнктивной, нормально формой(ПНФ) ПФ называется конъюнкция элементарных дизъюнкций:

Все дизъюнкции имеют ранг ПФ:

 

 

Тема 2.3. Логические элементы и схемы. Классификация

Логических устройств

Функционально полные системы логических функций

 

Функционально полной системой или базисом переключательных функций F₁,F₂,…,F_n с помощью которой может быть представлена любая функция алгебры логики. Функционально полными системами называются базисы:

1. Базис: И, ИЛИ, НЕ

2. Базис: И, НЕ

3. Базис: ИЛИ, НЕ

4. Базис (или базис Шеффера): И-НЕ

5. Базис (или базис Пирса): ИЛИ-НЕ

6. Базис: И-ИЛИ-НЕ

 

Базис И, ИЛИ, НЕ принято называть основным т.к. любая сложная ПФ может быть записана в виде СДНФ или СКНФ.

Базисы могут быть избыточными и минимальными:

1. Базис является избыточной, т.к. возможно исключение из него некоторых функций, например: используя законы двойного отрицания и Де-Моргана можно исключить, либо функцию И, заменяя её на ИЛИ, НЕ(Базис 3); либо ИЛИ, заменяя её на И, НЕ(Базис 2). Базисы 2, 3 называют нормальными(минимальными), т.к. при удалении из этих базисов хотя бы одной функции функционально полная система превращается в не полную.

 

Абстрактный автомат имеет один входной и один выходной каналы.

Под законом функционирования понимается совокупность правил описывающих последовательность переключения состояния Автомата и последовательность выходных сигналов в зависимости от последовательности входных сигналов.

В зависимости от способа определения значений выходных сигналов различают 2 типа автоматов:

1) Автоматы Мура описываются системой уравнений a(t+1)=q(a(t),z(t)); w(t)=Л(a(t))

В автоматах мура выходной символ не зависит явно от входного символа z(t) а переделяется внутренним состоянием Автомата

2) Автоматы Мили описываются системой уравнений a(t+1)=q(a(t),z(t)); w(t)=Л(a(t),z(t))

В автомате Мили выходной сигнал в момент времени t зависит как от внутреннего состояния автомата в момент t так и от входного сигнала в момент t.