
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напружений і деформований станСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Розглянемо навантажене тіло.
Поблизу точки А виділимо нескінченно малий паралелепіпед і розглянемо його окремо. До граней паралелепіпеда прикладені внутрішні сили, які замінюють дію відкинутої частини тіла. Повні напруження на гранях можна розкласти на три складові – проекції повних напружень на координатні вісі:
σ - нормальні напруження; τ – дотичні напруження.
Отже, на гранях елементарного паралелепіпеда, виділеного в околі точки навантаженого тіла, діють дев’ять компонент напружень. Запишемо їх у вигляді квадратної матриці:
де в 1-му, 2-му та 3-му рядках наведено складові напружень відповідно на площадках, перпендикулярних до осей x, y, z. Цю сукупність напружень називають тензором напружень.
Коли відомий тензор напружень, тобто сукупність напружень на трьох взаємно перпендикулярних площадках, то можна визначити напруження на будь-яких площадках, проведених в околі точки.
Нормальні напруження вважаються додатними, якщо вони спричинюють розтягання, від’ємними – якщо стискання.
Нехай напрям зовнішньої нормалі ν до площадки збігається з додатним напрямом будь-якої координатної осі. Тоді додатне нормальне напруження на цій площадці (на рисунку це
Запишемо рівняння рівноваги елемента щодо його обертання:
Складемо рівняння моментів відносно осі z. Сили, які паралельні цій осі і перетинають її, в рівняння не увійдуть. Моменти сил
Якщо два головних напруження не є нульовими, а одне дорівнює нулю, то такий напружений стан називається плоским.
Якщо всі три напруження не дорівнюють нулю, то це об’ємний напружений стан.
Лінійний напружений стан
Кут α – кут повороту вважаємо додатним, якщо він відраховується проти годинникової стрілки. На нахиленій площадці напруження паралельні осьовій силі N=P в перерізі
Проекціюючи
Максимальні дотичні напруження виникають при α=45º:
Правило знаків для дотичних напружень: дотичне напруження на площадці вважають додатним, якщо воно намагається повернути частину елемента, яка розглядається, відносно будь-якої точки, взятої всередині її за годинниковою стрілкою.
ЛЕКЦІЯ № Плоский напружений стан Плоский напружений стан виникає у випадку, коли два головних напруження не дорівнюють нулю, а третє дорівнює нулю. Нехай
Виділимо площадку α – переріз І-І, та β – переріз ІІ-ІІ. Переріз І-І провели під кутом β нормаль Напруження
Де З формул для лінійного напруженого стану:
знак
Використавши додавання остаточно знайдемо:
На площадці ІІ-ІІ проведем нормаль Тоді:
З цих рівнянь маємо, що:
Максимальне дотичне напруження:
В теорії плоско напруженого стану можна розмежувати дві основні задачі: пряма і зворотна.
Пряма задача. В точці відомі положення головних площадок, і відповідні до них головні напруження. Треба знайти нормальні і дотичні напруження, що діють на площадках, які нахилені під заданим кутом
Зворотна задача. В точці відомі нормалі й дотичні напруження, що діють у двох взаємно перпендикулярних площадках, що походять через дану точку. Треба знайти головні площадки та головні напруження.
Формули для обчислень:
Лекція №
|
|||||||||
|
Последнее изменение этой страницы: 2016-08-15; просмотров: 584; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.191.176.109 (0.008 с.) |






 ) також збігається з додатним напрямом координатної осі. Дотичні напруження на такій площадці вважаються додатними, якщо вони напрямлені в бік відповідних додатних напрямків координатних осей. Якщо зовнішня нормаль до площадки збігається з від’ємним напрямом координатних осей, всі три складові напруження на площадці вважаються додатними, коли вони напрямлені в бік від’ємних напрямів відповідних координатних осей.
) також збігається з додатним напрямом координатної осі. Дотичні напруження на такій площадці вважаються додатними, якщо вони напрямлені в бік відповідних додатних напрямків координатних осей. Якщо зовнішня нормаль до площадки збігається з від’ємним напрямом координатних осей, всі три складові напруження на площадці вважаються додатними, коли вони напрямлені в бік від’ємних напрямів відповідних координатних осей. = 0;
= 0;  = 0;
= 0; 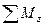 = 0.
= 0. на двох гранях, перпендикулярних до осі z, зрівноважуються, так само як і моменти сил
на двох гранях, перпендикулярних до осі z, зрівноважуються, так само як і моменти сил  на верхній та нижній гранях елемента. Отже, маємо:
на верхній та нижній гранях елемента. Отже, маємо: Напружений стан, в якому одне головне напруження відмінно від нуля, а два інших дорівнюють нулю, називають одновісним або лінійним.
Напружений стан, в якому одне головне напруження відмінно від нуля, а два інших дорівнюють нулю, називають одновісним або лінійним.
 ;
;  ;
;  (розтяг – стиск)
(розтяг – стиск)
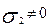 ;
; 

 В поперечних перерізах стержня нормальні напруження:
В поперечних перерізах стержня нормальні напруження:
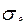
 На площадці, яка нахилена під кутом α, діють нормальні напруження та дотичні.
На площадці, яка нахилена під кутом α, діють нормальні напруження та дотичні. Площа поперечного перерізу стержня була
Площа поперечного перерізу стержня була  , після повороту площа площадки:
, після повороту площа площадки: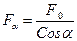
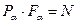

 на нормаль
на нормаль  до площадки і на площину перерізу, дістанемо:
до площадки і на площину перерізу, дістанемо:

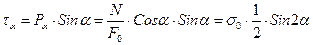

 ,
,  ,
, 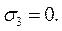
 Проведемо перерізи І-І, ІІ-ІІ, ІІІ-ІІІ, ІV-IV
Проведемо перерізи І-І, ІІ-ІІ, ІІІ-ІІІ, ІV-IV .Площадки (α) і (β) перпендикулярні.
.Площадки (α) і (β) перпендикулярні.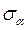 і
і  на площадці α будуть визиватись як дією
на площадці α будуть визиватись як дією  , так і дією
, так і дією  . Тоді застосовуючи принцип суперпозиції, тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів, можемо записати:
. Тоді застосовуючи принцип суперпозиції, тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів, можемо записати:

 і
і  -напруження, що спричинені дією
-напруження, що спричинені дією  ; а
; а  і
і  - напруження, що спричиняються дією
- напруження, що спричиняються дією  .
. ;
; 
 Для визначення
Для визначення 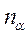 утворює з напруженням
утворює з напруженням  кут
кут  . Тоді
. Тоді 

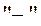 так як відрахунок ведеться за годинниковою стрілкою. Тоді
так як відрахунок ведеться за годинниковою стрілкою. Тоді ;
; 



 кут
кут  .
.
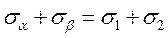 ─ сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від кута нахилу цих площадок і дорівнює сумі головних напружень.
─ сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від кута нахилу цих площадок і дорівнює сумі головних напружень. ─ ця рівність виражає закон парності дотичних напружень.
─ ця рівність виражає закон парності дотичних напружень. ,
,  .
. до головних;
до головних;






