
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Напруження стиску під кутом до волоконСодержание книги
Поиск на нашем сайте
6.9.1Слід враховувати взаємодію між стискальними напруженнями у двох або більше напрямах. 6.9.2Стискуючі напруження під кутом a до волокон (див. рис. 6.5) повинні задовольняти наступній умові:
де: sс,a,d – напруження стиску під кутом до волокон (визначається за 6.9.3); fс, 0 ,d та fс, 90 ,d - розрахункові опори стиску вздовж та поперек волокон відповідно (визначаються згідно п. 3.4); kс, 90 - коефіцієнт, що враховує вплив напружень поперек волокон (див. 6.1.5).
Рисунок. 6.5 - Напруження стиску під кутом до волокон 6.9.3Стискальні напруження під кутом a до волокон слід визначати за формулою:
де: Fс,a,d – розрахункова стискаюча сила під кутом до волокон a; Розтяг поперек волокон 6.10.1При розтязі поперек волокон повинна задовольнятись наступна умова: s t ,90, d £ ft ,90, d , (6.44) де s t ,90, d - розрахункове напруження розтягу поперек волокон (визначається за п. 6.10.2); ft ,90, d - розрахунковий опір розтягу поперек волокон (визначається згідно п. 3.4). 6.10.2Розрахункове напруження розтягу поперек волокон слід визначати за формулою:
в якій Ft ,90, d – розрахункове зусилля розтягу поперек волокон; Aef – розрахункова площа контакту поперек волокон. 6.10.3При розтягу поперек волокон слід враховувати вплив розмірів елемента як?. РОЗРАХУНОК ЕЛЕМЕНТІВ ДЕРЕВ’ЯНИХ КОНСТРУКЦІЙ ЗА ГРАНИЧНИМИ СТАНАМИ експлуатаційної здатності Піддатливість вузлів 7.1.1 Для вузлів з використанням кріпильних деталей дюбельного типу (цвяхи, шурупи, гвинти, скоби, зубчасті пластини, шпонки) модуль жорсткості Kser для площини зсуву на кріпильну деталь при експлуатаційному навантаженні береться з таблиці 12.1 при ρm в кг/м3, і d або dc, в мм. Значення dc встановлені в EN 13271. Примітка. В EN 26891 символ Ks використовується замість Kser. Таблиця 7.1 - Значення Kser для кріпильних деталей і конекторів в Н/мм, для з'єднань деревина-деревина і деревина до панелі на основі деревини
7.1.2 Якщо середні значення щільності двох з'єднувальних елементів на основі деревини є різними (ρm ,1 і ρm, 2), тоді ρm у вищевказаному виразі слід прийняти як
7.1.3 За наявності з'єднань: сталь до деревини або бетон до деревини, Kser має бути заснований на ρm для дерев'яного елементу і помножений на 2,0. Граничні прогини балок Таблиця 7.1 – Рекомендовані значення граничних прогинів
7.2.1 У ДСТУ-Н Б EN 1995-1-1 розрахункове експлуатаційне навантаження, що використовується для визначення прогину за граничними станами експлуатаційної здатності (SLS), визначається характеристичним поєднанням впливів. 7.2.2 Миттєвий прогин uinst для елемента суцільного перерізу, що працює окремо від інших конструкцій, повинен розраховуватися з використанням характеристичного поєднання впливів, відповідного середній величині модуля пружності вздовж волокон E 0, mean та/або середнього значення модуля зсуву Gmean. Для дерев’яних елементів 7.2.3 Загальний прогин ufin отримують шляхом підсумовування миттєвого прогину, обчислюваного відповідно до п. 7.1 і прогину від повзучості. При визначенні загального прогину слід керуватися положеннями цього розділу норм. 7.2.4 Якщо елемент згинається при дії поперечної сили, на додаток до прогину від згинального моменту, повинен бути визначений прогин від цієї сили. 7.2.5 Прогин від зсуву може бути виражений у величинах прогину від згину, помножений на коефіцієнт, що враховує вплив зсуву. Значення коефіцієнта для вільно опертої балки прямокутного перерізу шириною b, висотою h і розрахунковим прольотом l для стандартних випадків завантаження наведено в таблиці 7.2. Загальний прогин від зсуву і згину в балці для прийнятого випадку завантаження, визначається шляхом множення прогину від згину на супутній підвищуючий коефіцієнт, що враховує вплив зсуву.
Таблиця 7.2 – Рекомендовані формули для визначення прогину шарнірно опертих балок прямокутного поперечного перерізу від згину і підвищуючих коефіцієнтах з урахуванням зсуву
7.2.6 Розрахунок прогину в шарнірно опертих односхилих і двосхилих клеєних балках. Для визначення прогину в середині прольоту шарнірно опертих односхилих і двосхилих балок від дії згинального моменту і поперечної сили, при дії зосередженої сили в середині прольоту або рівномірно розподіленого навантаження по довжині балки кожного з типів, можуть бути рекомендовані вирази, які наведені в таблиці 7.3. Таблиця 7.3 – Рекомендовані формули для визначення прогину шарнірно опертих однопрогонових односхилих і двосхилих балок
Коливання елементів 7.3.1 При розрахунку згинальних елементів за граничними станами експлуатаційної придатності необхідно перевірити, що впливу, яким можуть піддаватися елементи, а також їх складові частини або споруда в цілому, не викликають коливань, які негативно впливають на роботу споруди і не створюють дискомфорту у людей. 7.3.2 Дискомфорт може бути обумовлений наступним: – коливаннями, що виникають від працюючої машини (механізму); – коливаннями, що виникають при ходьбі; – коливаннями, що виникають через близькість знаходження джерела коливань.
7.3.3 Відповідно до вимог ДСТУ-Н Б EN 1995-1-1, що стосуються розрахунку дерев'яних перекриттів, необхідно гарантувати, що їх поведінка при даному навантаженні, що викликає коливання конструкції, залишається в рамках допустимих меж по SLS. 7.3.4 Допустимі рівні безперервних коливань у конструкції по відношенню до впливу на людину, що виникають внаслідок роботи механізмів, можуть прийматися на підставі ISO 2631:2. Якщо коливання від механізму перевищують допустимий рівень, то найбільш поширеним способом вирішення проблеми, є пристрій окремих від конструкції фундаментів під механізм, або установка віброізоляторів між механізмом і конструкцією. Дані рішення повинні враховуватися при розрахунку конструкцій. 7.3.5 При розрахунку перекриттів житлових будинків повинні враховуватися коливання, що виникають при ходьбі. У ДСТУ-Н Б EN 1995-1-1 розрахункові вимоги поширюються виключно на конструкції перекриттів житлових будівель, що мають частоту власних коливань більш 8Гц. Для перекриттів з частотою власних коливань менше 8 Гц, вказано на проведення додаткових досліджень. 7.3.6 У житлових будинках для прямокутних у плані перекриттів, з власною частотою понад 8 Гц і розмірами l × b, вільно опертих по чотирьох сторонах, виконаним по дерев'яних балках прольотом l, значення частоти власних коливань f 1 може бути визначено з виразу (7.2):
де l – розрахунковий проліт балки перекриття, м; (EI) l – еквівалентна згинна жорсткість конструкції, підтримуючої перекриття, щодо осі, перпендикулярної напрямку прольоту балки, Н м2/м; m – маса на одиницю площі, кг/м2, яка визначається від постійних навантажень. Якщо настил перекриття не розрахований на спільну роботу з балками перекриття, то (EI) l повинна залежати тільки від згинальної жорсткості балок перекриття. Врахування настилу при визначенні (EI) l можливий у випадках, коли він жорстко з'єднаний з дерев'яними балками перекриття, тобто з'єднаний на клею і розраховувався як обшивка плит перекриття у відповідності з 9.1.2 ДСТУ-Н Б EN 1995-1-1; 7.3.7 У житлових будинках основним типом перекриттів, виконаних з дерев'яних конструкцій, є балочні перекриття. При розрахунку таких перекриттів повинні розглядатися: – низькочастотні ефекти (ефект від частоти кроку при ходьбі); – високочастотні ефекти (ударний ефект від п'яти при ходьбі). 7.3.8 Вимушені коливання перекриття від дії частоти кроку будуть менше 8 Гц, що еквівалентно статичному навантаженню. Прогин у центрі перекриття від дії статичного навантаження в 1 кН і прикладеного в даній точці, що моделює ефект від сили, з якою тисне нога людини на перекриття, повинен бути не більше:
u £ 1,8 мм - при довжині прольоту £ 4000 мм (7.3)
де u – прогин балки, мм; l – проліт балки перекриття, мм. Прогин перекриття u, при дії зосередженого навантаження в середині прольоту перекриття з розрахунковим прольотом lef, може визначатися з виразу:
де kdist – переводить навантаження 1кН в навантаження на одну балку; lef – розрахунковий прольот балки перекриття в мм; для вільно опертих балок lef повинен бути прийнятий рівним прольоту l; для крайніх прольотів нерозрізних балок leg = 0,9 l, а для середніх прольотів – lef = 0,851 l; kamp – підвищувальний коефіцієнт, що враховує вплив зсуву на прогин у разі використання суцільних дерев'яних і клеєних балок, або піддатливість з'єднання у разі використання механічних зв'язків; EIjoist – згинна жорсткість балки в Н мм2, що розраховується з використанням середнього значення модуля пружності балки E 0, mean . Значення коефіцієнта kamp приймаються рівними: 1,05 – для шарнірно опертих суцільних дерев'яних балок; 1,1 – для нерозрізних суцільних дерев'яних балок; 1,15 – для шарнірно опертих двотаврових клеєних балок з тонкою стінкою; 1,3 – для нерозрізних двотаврових клеєних балок з тонкою стінкою; 1,3 – для вільно опертих ферм покриття на механічних зв'язках у з'єднаннях; 1,45 – для нерозрізних ферм покриття на механічних зв'язках в з'єднаннях. Значення коефіцієнта kdist для нерозрізних ферм покриття на механічних зв'язках в з'єднаннях слід визначати наступним чином:
де (EI) b – згинна погонна жорсткість перекриття, Н мм2/м; s – крок балок, мм. Примітка 1. Згинна жорсткість обчислюється як (EI) b з використанням середнього значення модуля пружності перекриття, а неоднорідності на кінцях перекриття можуть бути проігноровані. 7.3.9 При дії величини імпульсного навантаження в 1 Н в центрі перекриття, моделює контакт п'яти людей, максимальне початкове значення вертикального коливання (швидкості переміщення) перекриття v (м/с), має задовольняти умові 7.7 ДСТУ-Н Б EN 1995-1-1:
де v – величина імпульсної швидкості в м / (Н с2), тобто граничне значення швидкості коливання (м / с) у вертикальному напрямку, викликаної імпульсом у 1 Н с, моделюючим випадок впливу п'яти людей, діючої на перекриття, при максимальному переміщенні; b – постійна величина для контролю значення реакції імпульсу в залежності від прогину a перекриття, як показано на рисунку 7.2 в ДСТУ-Н Б EN 1995-1-1. Значення b може бути виражене таким чином:
тут u – прогин в мм, який визначається з виразу (7.5); f 1 – частота власних коливань перекриття в Гц, яка визначається з виразу (7.2); ζ – модальний декремент загасання коливань перекриття, який для перекриттів приймається 0,02. 7.3.10 При обчисленні фактичної величини імпульсної швидкості конструкції, повинні дотримуватися такі вимоги ДСТУ-Н Б EN 1995-1-1: – для прямокутних перекриттів з розмірами в плані b x l і вільно опертих по чотирьох сторонах, середнє значення v може бути визначено з виразу (7.10) в ДСТУ-Н Б EN 1995-1-1 наступним чином:
де b – ширина перекриття, м; l – розрахунковий проліт перекриття, м; m – визначається в кг/м2; n 40 – номер першої форми коливання з власною частотою до 40 Гц. – значення n 40 визначається з виразу (7.11) ДСТУ-Н Б EN 1995-1-1:
де (EI) l – еквівалентна згинна жорсткість перекриття за напрямом прольоту балок в Нм2/м. При цьому (EI) b <(EI) l. ЕЛЕМЕНТИ І КОНСТРУКЦІЇ
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 245; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.227.73 (0.011 с.) |

 , (6.42)
, (6.42)
 , (6.43)
, (6.43)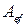 - розрахункова площа контакту під кутом a до волокон.
- розрахункова площа контакту під кутом a до волокон.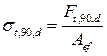 , (6.45)
, (6.45)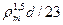




 (7.1)
(7.1)



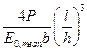


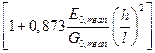


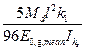











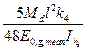

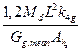
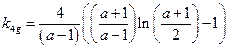
 , (7.2)
, (7.2) , мм - при довжині прольоту > 4000 мм (7.4)
, мм - при довжині прольоту > 4000 мм (7.4) , (7.5)
, (7.5)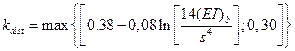 , (7.6)
, (7.6) , (7.7)
, (7.7) (7.8)
(7.8) (7.9)
(7.9) , (7.10)
, (7.10)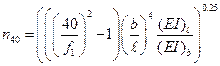 , (7.11)
, (7.11)


