
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок клеєних балок з плоскими фанерними стінкамиСодержание книги
Поиск на нашем сайте
8.3.1 Перерізи клеєних балок з плоскими фанерними стінками складаються з елементів, склеєних разом. При використанні таких перерізів розрахункові передумови базуються на принципі, що між елементами в перерізі не виникне зсувів ні в одному з швів. Даний принцип складає основу правил розрахунку, приведених в розділі 9 ДСТУ-Н Б EN 1995-1-1. 8.3.2 У клеєних балках з плоскими фанерними стінками полиці можуть бути виконані з конструкційної деревини, LVL або шаруватої клеєної деревини, а стінки – з фанери. Поперечний переріз таких балок може бути двотавровим або коробчастим (рис. 8.5). Для клеєних складених перерізів потрібний високий рівень контролю, що досягається в заводських умовах.
а) – коробчастий переріз; б) – двотавровий переріз; в) – розподіл нормальних напружень в перерізі балки при згині Рисунок 8.5 – Напруження в перерізі балки з тонкою стінкою 8.3.3 Головною відмінністю між розрахунком, використовуваним для складених перерізів, і використовуваним для суцільних перерізів, є те, що мала деформація по теорії згину повинна корегуватися з урахуванням того, що складені перерізи складаються з елементів, що мають різні значення модуля пружності. Це повинно враховуватися при розрахунку характеристик міцності і жорсткості. 8.3.4 Для розрахунку перерізів балок з плоскими фанерними стінками використовується метод еквівалентного (приведеного перерізу). Відповідно до даного методу, один з матеріалів в складеному перерізі приймається як основний, а інші - еквівалентні. При використанні даного методу формується однорідний еквівалентний переріз, до якого застосовна теорія згину. Для матеріалу, який був перетворений, напруження розраховують шляхом множення напружень згину в однорідному еквівалентному перерізі на відношення модуля пружності реального матеріалу в складеному перерізі до модуля пружності вибраного матеріалу. Таке відношення називають модульним відношенням. В процесі розрахунків для кожного матеріалу слід використовувати середнє значення модуля пружності Emean . 8.3.5 При розрахунку перерізів балок з плоскими фанерними стінками по граничних станах несучої здатності відповідно до вимог ДСТУ-Н Б EN 1995-1-1 за розрахункові значення модулів пружності і зсуву, для умови миттєвого стану, приймаються їх середні значення, тобто Ed,uls = Emean, Gd,uls = Gmean, (8.30) а для стану, що враховує кінцеве середнє значення жорсткості
де: Ed,uls – розрахункове значення модуля пружності для ULS; Gd,uls – розрахункове значення модуля зсуву для ULS; Emean – середнє значення модуля пружності матеріалу елементу; Gmean – середнє значення модуля зсуву матеріалу елементу; kdef – коефіцієнт деформації для деревини і матеріалів на її основі. Значення kdef для деревини і матеріалів на її основі визначають по ДСТУ-Н Б EN 1995-1-1 (таблиця 3.2) ψ2 – коефіцієнт для практично постійного значення змінної впливів навантаження, що викликає найбільше напруження відносно міцності. Якщо це постійний вплив, то ψ2 = 1, а для змінних впливів значення ψ2 приймається за ДСТУ-Н Б EN 1995-1-1. 8.3.6 Для перерізів, приведених на рис. 8.5, еквівалентна площа поперечного перерізу Aef і момент інерції Ief визначаються за формулами: – для миттєвого стану
– для стану, що враховує кінцеве середнє значення жорсткості: а) якщо розрахункова умова виникає від дії постійного навантаження:
б) якщо розрахункова умова виникає від дії змінного навантаження Qi:
де: ψ2, i і ψ2 – коефіцієнт для практично постійного значення змінної дії Qi; If – момент інерції перерізу обох полиць відносно нейтральної осі; Iw – момент інерції перерізу незміненої стінки відносно нейтральної осі. При дії розрахункового згинального моменту Md, якщо модуль пружності стінки менший, ніж полиці, напруження від згину в полиці зростатиме, а в стінці – зменшуватиметься з часом. Для даної умови необхідно перевірити лише напруження в полицях в кінцевому стані з середніми значеннями пружних характеристик, а також напруження в стінках в миттєвому стані. Проте, якщо модуль пружності стінки більше модуля пружності полиці, нормальні напруження від згину слід перевіряти в миттєвому стані в полицях і в кінцевому стані, з середніми значеннями пружних характеристик в стінці. При розгляді симетричних перерізів істотної відмінності спостерігатися не буде між відповідними значеннями геометричних параметрів в обох станах, і отже відмінності в напруженнях будуть відносно невеликими. 8.3.7 Визначення напружень в полицях балки слід робити відповідно до вимог ДСТУ-Н Б EN 1995-1-1. а) Напруження від згину. Максимальне значення нормальних напружень від згину балки виникатиме в крайніх шарах волокон на відстані y 1 і y 2 від нейтральної осі (рис. 8.5 в). Якщо переріз симетричний відносно осі в-в, то відстані від нейтральної осі до крайніх волокон розтягнутої і стислої зон будуть рівні між собою, тобто y 1 = y 2, інакше y 1 і y 2 матимуть різні значення. Якщо переріз не симетричний відносно осі у-у, положення нейтральної осі відрізнятиметься в миттєвому і кінцевому станах, а відповідні значення y 1 і y 2 в цих станах також розрізнятимуться. Для обліку цих відмінностей були прийняті наступні позначення: y 1 ,inst і y 2 ,inst – для миттєвого стану, а y 1 fin і y 2 fin – для кінцевого стану з середніми значеннями модуля пружності. Максимальне розрахункове напруження внаслідок згину в стислій зоні на відстані y 1 визначається: – у миттєвому стані
– у кінцевому стані з середніми значеннями
Максимальне розрахункове напруження розтягу в розтягнутій зоні на відстані y 2 визначається: в миттєвому стані
у кінцевому стані з середніми значеннями
Згідно ДСТУ-Н Б EN 1995-1-1 (9.1.1(1)) для забезпечення міцності перерізу повинна дотримуватися умова, щоб розрахункові значення напружень, визначені за формулами (8.39 і 8.40), були менші або дорівнювали розрахунковому значенню міцності при згині fm,d, тобто σ f,inst,c,max,d, σ f,fin,c,max,d, і σ f,inst,t,max,d, σ f,fin,t,max,d ≤ f m,d, (8.41) де: fm,d – розрахункове значення міцності матеріалу полиці. б) Напруження стиску з врахуванням стійкості. Згідно ДСТУ-Н Б EN 1995-1-1 стійкість балки забезпечується виключно міцністю при поздовжньому згині стислої полиці. Розрахункова вимога полягає в тому, щоб величина стискаючого напруження в полиці дорівнювала б або була б менше значення міцності при стиску. Величина напруження стиску приймається рівною середньому значенню, яке визначається за формулами: – в миттєвому стані
– у кінцевому стані з середніми значеннями
Згідно з вимогами ДСТУ-Н Б EN 1995-1-1 для забезпечення міцності перерізу з врахуванням стійкості повинна дотримуватись умова, щоб розрахункові напруження були менші або дорівнювали розрахунковому значенню міцності при стиску kc fc,0,d, тобто σ f,inst,c,d і σ f,fin,с,d ≤ k c f c,0,d, (8.43) де: fc,0,d – розрахункове значення міцності при стискуванні матеріалу полиці; kc – коефіцієнт поздовжнього згину, значення якого визначається з припущення, що стисла полиця працює як центрально-стиснутий стрижень, закріплений на кінцях від поперечного переміщення. Переріз традиційно приймається суцільним прямокутним висотою b. При повному закріпленні полиці kc = 1. в) Напруження розтягу. Полиця також має бути перевірена, щоб середнє розрахункове значення напруження розтягу в розтягнутій полиці було рівним або менше розрахункового значення міцності при розтягу. Розрахункове напруження розтягу визначається за формулою: в миттєвому стані
у кінцевому стані з середніми значеннями
Згідно з вимогами ДСТУ-Н Б EN 1995-1-1 для забезпечення міцності перерізу повинна виконуватися наступна умова σ f,inst,t,d і σ f,fin,t,d ≤ f t,0,d, (8.45) де: ft,0,d – розрахункове значення міцності для матеріалу полиці при розтягу вздовж волокон; σ f,inst,t,d і σ f,fin,t,d – розрахункові значення напруження, визначені за формулами (8.44). 8.3.8 Визначення напружень в стінці балки має здійснюватися відповідно до вимог Стінка балки має бути перевірена на міцність по напруженням стиску та розтягу від згину балки, на міцність з'єднань (стиків) листів стінки, на міцність з врахуванням поздовжнього згину від дії напруження зсуву, тобто, що клейові шви між стінкою і полицями здатні передати горизонтальне напруження зсуву в перерізі. а) Визначення нормального напруження від згину балки Максимальні нормальні напруження що виникають в стінці від згину балки слід визначати за формулами: максимальне стискуюче напруження: - в миттєвому стані
- у кінцевому стані з середніми значеннями
максимальна напруження розтягу: - в миттєвому стані
- у кінцевому стані з середніми значеннями
Згідно з вимогами ДСТУ-Н Б EN 1995-1-1:2008/2011 для забезпечення міцності перерізу повинні дотримуватися наступні умови: σ w,inst,c,d і σ f,fin,c,d ≤ f c,w,d, (8.48) σ w,inst,t,d і σ f,fin,t,d ≤ f t,w,d, (8.49) де: та
Складові формул були визначені вище, а fc,w,k і ft,w,k – характеристичні значення міцності при стиску і розтягу матеріалу стінки відповідно. б) Перевірка напружень з врахуванням поздовжнього згину. При розрахунку стінки відповідно до вимог ДСТУ-Н Б EN 1995-1-1 повинні виконуватись наступні умови: якщо hw ≤ 70 bw, (8.52) та
де: Fv,w,Ed – розрахункова поперечна сила, що діє на кожну стінку; значення інших параметрів були визначені вище. в) Напруження зсуву в клейових швах між стінками і полицями. Напруження зсуву виникають на полиці і розподіляються між стінкою і полицями через клейову поверхню з'єднання. Розрахункові значення напружень зсуву визначаються таким чином: - в миттєвому стані
- у кінцевому стані з середніми значеннями
де: τ inst,mean,d, τ fin,mean,d – розрахункові значення напружень зсуву в миттєвому (і остаточному) випадку деформування на клейовій поверхні між полицею і стінкою; Vd – розрахункове значення сили зсуву в області максимального зсуву; S f,inst, S f,fin – статичний момент площі полиці (без врахування площі стінки) відносно нейтральної осі в миттєвому (і остаточному) випадку деформації; hf – висота полиці, тобто hf,c або hf,t, якщо відповідають; n – число площин клейового шва між стінкою і полицею. Для врахування концентрації напружень на поверхні стінки/полиці в області точки 2 (Рис. 8.5 а і б), якщо висота стінки більш ніж 4 b ef, то згідно ДСТУ-Н Б EN 1995-1-1 мають виконуватися наступні умови
де: fv,90,d – розрахункове значення міцності матеріалу стінки при сколюванні; інші параметри були визначені вище;
Елементи з підрізкою 8.4.1Загальні положення 8.4.1.1 При перевірці міцності елементів повинно враховуватись концентрація напружень у підрізках. 8.4.1.2 Впливом концентрації напружень можна знехтувати у наступних випадках: - при розтягу або стиску вздовж волокон при кутах менше 12°; - при згині з напруженнями розтягу у підрізці, якщо перехід до звуження не крутіше ніж 1: і = 1:10, тобто і ³ 10 (рисунок 8.6 а); - при дії згину із напруженнями стиску у підрізці (рисунок 8.6 б).
а б Рисунок 8.6 – Згин у підрізці 8.4.2Балки з підрізкою на опорах 8.4.2.1 Для балок прямокутного перерізу при умові, коли волокна розташовані практично вздовж елемента, напруження зсуву на опорі у підрізці повинні визначатись із використанням фактичної (зменшеної) висоти hef (рис. 8.7). 8.4.2.2 Необхідно перевіряти умову
де kv – коефіцієнт зниження, що визначається: - для балок з підрізкою зверху і знизу (рис. 8.7 б) kv = 1,0 (8.58) - для балок із підрізкою знизу (рис. 8.7 а)
де і – нахил підрізки (рис. 8.7 а); h – висота балки, мм; х – відстань від лінії дії опорної реакції до початку підрізки; a = hef / h,
а б Рисунок 8.7 – Балки з підрізками на опорах Міцність системи 8.5.1 Коли кілька елементів конструкції однакового прольоту або збірні елементи розкріплені з одного боку системою в'язей, характеристики міцності елемента можуть бути помножені на коефіцієнт міцності системи ksys. 8.5.2 Передбачена система в’язей забезпечує перерозподіл зусиль від одного елемента до інших, при цьому коефіцієнт ksys приймається 1,1. 8.5.3 Перевірка міцності системи в’язей повинна виконуватися за умови дії короткочасних навантажень. Примітка - Для кроквяних ферм з максимальною відстанню між центрами вузлів 1,2 м можна прийняти, що обрешітка, прогони або панелі можуть передавати навантаження на сусідні ферми, забезпечуючи безперервність розподілу навантаження на двох останніх прольотах, при коливанні будь-якого вузла. 8.5.4Для настилів з клеєної деревини або перекриттів можуть використовуватися значення ksys, наведені на рис. 8.8.
n= bef / blam bef = Mbeam / mplate Число навантажених ламелей 1 - ламелі з фіксацією цвяхами або шурупами; 2 - ламелі склеєні Рисунок 8.8 - Коефіцієнт міцності системи ksys для ламінованих листів настилу з цільної або клеєної деревини
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 401; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.219.203 (0.012 с.) |


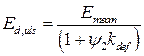 , (8.31)
, (8.31) , (8.32)
, (8.32) (8.33)
(8.33) (8.34)
(8.34) (8.35)
(8.35) (8.36)
(8.36) (8.37)
(8.37) (8.38)
(8.38) (8.39 а)
(8.39 а) (8.39 б)
(8.39 б) (8.40 а)
(8.40 а) (8.40 б)
(8.40 б) (8.42 а)
(8.42 а) (8.42 б)
(8.42 б) (8.44 а)
(8.44 а) (8.44 б)
(8.44 б) (8.46 а)
(8.46 а) (8.46 б)
(8.46 б) (8.47 а)
(8.47 а) (8.47 б)
(8.47 б) (8.50)
(8.50) (8.51)
(8.51)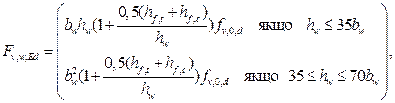 (8.53)
(8.53) (8.54 а)
(8.54 а) (8.54 б)
(8.54 б)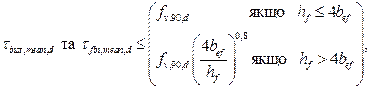 (8.55)
(8.55) (8.56)
(8.56)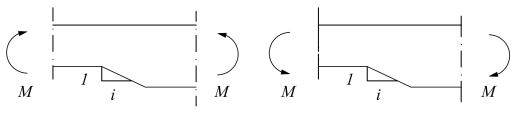
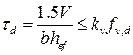 , (8.57)
, (8.57) , (8.59)
, (8.59) , (8.60)
, (8.60)




