
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Елементи що працюють на ЗгинСодержание книги
Поиск на нашем сайте
6.4.1 Розрахунок міцності елементів що працюють на згин в площині однієї осі перерізу, розкріплених від втрати стійкості плоскої форми деформування, по нормальним напруженням слід виконувати за формулою:
де sm , y, d - розрахункове напруження згину (визначається за формулою (6.16)); fm , y, d – розрахункове значення міцності при згині (визначаються згідно п. 3.2.1). Розрахункове напруження від згину слід визначати за формулою:
де Мd – розрахунковий згинальний момент; Wd - розрахунковий момент опору поперечного перерізу. При наявності ослаблень Wd = Wnet визначається за умови, що всі ослаблення на ділянці довжиною 15 см суміщаються в одному розрахунковому перерізі. 6.4.2 Розрахунок елементів, що працюють на згин на міцність по сколюванню слід виконувати за формулою: td £ fv,d, (6.17) де: td - розрахункове напруження сколювання (визначається за формулою (6.18)); fv,d - розрахункове значення міцності при сколюванні (визначаються згідно п. 3.2.1). Розрахункові напруження сколювання слід визначати за формулою:
де: Sbr – статичний момент (брутто) частини перерізу, що зсувається, відносно нейтральної осі; Ibr – момент інерції перерізу (брутто) відносно нейтральної осі; bef – розрахункова ширина перерізу елементу. При визначенні напружень сколювання для елементів прямокутного перерізу необхідно враховувати вплив тріщин шляхом застосування розрахункової ширини поперечного перерізу елемента: bef = kcr×b,(6.19) де b – ширина розрахункового поперечного перерізу; kcr× - коефіцієнт, що враховує вплив тріщин. Рекомендується приймати наступні значення коефіцієнту kcr: kcr = 0.67 – для суцільної та клеєної деревини; kcr = 1.0 – для інших матеріалів на основі деревини у відповідності з EN 13986 та EN 14374. 6.4.3 Розрахунок міцності елементів що працюють на косий згин по нормальним напруженням слід виконувати за формулами:
де sm , y, d та sm , z, d - розрахункові напруження згину відносно відповідних осей (визначається за формулою (6.16)); fm , y, d та fm , z, d - розрахункові значення міцності при згині (визначаються згідно п. 3.2.1). Примітка. Коефіцієнт km враховує перерозподіл напружень і вплив неоднорідності матеріалу в поперечному перерізі. Величина коефіцієнту km приймається наступним чином: Для суцільної деревини, клеєної деревини та LVL: - для прямокутного перерізу: km = 0,7; - для інших видів поперечного перерізу: km = 1,0. Для інших будівельних виробів на основі деревини для всіх поперечних перерізів: km = 1,0. 6.4.4Перевірку стійкості плоскої форми деформування елементів що працюють на згин слід виконувати за формулою: sm,d £ kcrit×fm,d, (6.22) де: sm,d – розрахункове напруження від згину (визначається за формулою (6.16)); fm , d - розрахунковий опір згину (визначається згідно п. 3.4), kcrit – коефіцієнт, що враховує втрату стійкості плоскої форми деформування (визначається згідно п. 6.4.4.1). 6.4.4.1 Для елементів з початковим викривленням з площини дії моменту М в межах пропорційності, kcrit можна визначити на основі виразу (6.23).
Коефіцієнт kcrit можна прийняти як 1,0 для елемента, в якому бокові переміщення стиснутої грані виключені по всій довжині, а на опорах не припускається кручення. 6.4.4.2Відносна гнучкість при згині:
де: sm,crit – критичне напруження від згину, визначене у відповідності з класичною теорією стійкості, враховуючи п’ятивідсоткові значення модуля жорсткості. Критичне напруження від згину можна визначити так:
де: Е 0,05 – п’ятивідсоткове значення модуля пружності деревини вздовж волокон; G 0,05 – п’ятивідсоткове значення модуля зсуву деревини вздовж волокон; Iz – момент інерції перерізу з площини згину; Itor – крутильний момент інерції перерізу; lef – розрахункова довжина елемента, що залежить від умов закріплення та конфігурації навантаження, у відповідності до п. 6.3.5; Wy – момент опору перерізу в площині згину. Для шпилькових порід деревини з суцільним прямокутним поперечним перерізом sm,crit можна приймати як:
де: b – ширина поперечного перерізу елементу, h – висота поперечного перерізу елементу. 6.4.4.3Коефіцієнт kcrit для шпилькових порід деревини з суцільним прямокутним поперечним перерізом можна визначати:
де: fm , k – характеристичне значення міцності деревини при згині.
|
||||
|
Последнее изменение этой страницы: 2016-04-08; просмотров: 233; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.118.214 (0.005 с.) |

 , (6.15)
, (6.15) , (6.16)
, (6.16) , (6.18)
, (6.18) , (6.20)
, (6.20) , (6.21)
, (6.21) . (6.23)
. (6.23) , (6.24)
, (6.24) , (6.25)
, (6.25)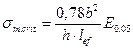 , (6.26)
, (6.26) , (6.27)
, (6.27)


