
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Умова жорсткості при крученніСодержание книги
Поиск на нашем сайте
ЛЕКЦІЯ №
Розтяг - стиск Розтяг або стиск стержня спричинюється силами, що діють уздовж його осі. У цьому випадку в поперечних перерізах стержня із шести внутрішніх силових факторів виникає лише один - поздовження (осьова сила
Для визначення сили Епюра - це графік (діаграма), яка показує як змінюється внутрішні зусилля при переході від перерізу до перерізу стержня. Правила побудови епюри: 1. Розбиваємо на ділянки. 2. Вісь (базу), на якій будується епюра, завжди вибирають так, щоб вона була паралельна або просто збігалась з віссю стержня. 3. Ординати на епюрі відкладають від осі епюра по перпендикуляру. 4. Штрихують епюри лініями, що перпендикулярні до бази. 5. Величини відкладають в певних масштабах
Поздовж сила вважається додатною, якщо вона спричинює розтяг, та від'ємною, якщо спричинює стискання. Наприклад:
Але можна визначати реакції Ra коли будемо йти з вільного кінця.
Розсічемо стержень довільним поперечним перерізом
Статична сторона задачі:
З цього рівняння не можна визначити напруження
Геометрична сторона задачі:
перерізи стержня плоскі до деформації, залишаються плоскими і після неї, переміщуючись поступово вздовж осі стержня (гіпотеза плоских перерізів)
подовжуються на одну і ту саму величину
і їхні відносні подовження
Фізична сторона задачі: полягає у встановленні залежності між деформаціями та напруженнями. При пружних деформаціях ця залежність лінійна і називається законом Гука.
Е - модуль пружності першого роду, або модуль Юнга. Це одна х фізичних констант матеріалу, виражається в Па Для однорідного та ізотропного матеріалу Е - стала величина тоді
Якщо Якщо Визначимо деформацію стержня
—з-н Гука для абсолютних подовжен
Добуток ЕГ називається жорсткістю поперечного перерізу стержня при розтягу - ділянці поздовжня сила та поперечний переріз змінні, то
Розглянемо поперечну деформацію стержня
-абсолютна поперечна деформація стержня
При розтяганні поперечні деформації від'ємні, а при стисканні додатні.
—відносна поперечна деформація.
Коефіцієнт Пуасона - безрозмірна величина, яка характеризує пружні властивості матеріалу, перебуває в межах від 0 до 0,5. Для Корки (пробка) він для сталі 0,3 для научики 0,5
Умова міцності при розтягу - стиску
п -коефіцієнт запасу міцності
Види розрахунків з використання умови міцності: 1. Проектувальний розрахунок За відомими навантаженнями для вибраного матеріалу знайти з умови міцності розміри поперечного перерізу стержня. Дані: 2. Перевірочний розрахунок За відомими розмірами та матеріалом деталі перевірити, чи зможе вона витримати задане навантаження
3. Визначення вантажопідйомності За відомими розмірами деталі, матеріалом і схемою навантажування визначити допустиме навантаження
ЛЕКЦІЯ № ДІАГРАМА РОЗТЯГУ
При проектуванні і розрахунках на міцність треба знати властивості матеріалів. Тому матеріали випробовують на розтяг, стиск, зсув, кручення, згин та твердість. Одним із основних видів випробовувань матеріалів є випробовування на розтяг, оскільки при цьому виявляються найбільш важливі їхні властивості. Для цього використовують спеціальні циліндричні зразки, котрі приєднують до установки та розтягують до розриву.
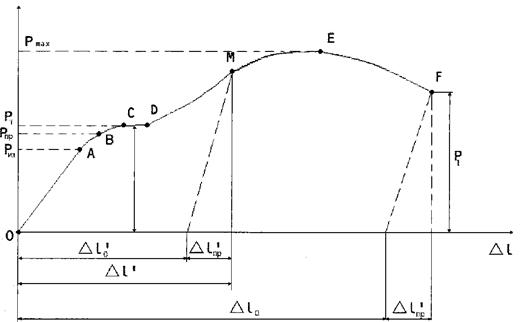
В процесі навантаження самописцем будується діаграма розтягу: де по осі ординат відкладається зусилля, а по осі абсцис - відповідні подовження. Типовий вигляд такої діаграми має:
Від початку навантаження до певного значення сили має місце прямо пропорційна залежність між подовженням зразка та силою. На діаграмі ця ділянка О А на ній справедливий закон Гука. Позначимо силу за якої закон пропорційності припиняє свою дію через Рну. На діаграмі це точка А. напруження, яке спричинюється силою Рну називається границею пропорційності.
Тобто границею пропорційності називається напруження, після якого порушується закон Гука. Позначимо через Рпр найбільше значення сили, при якому зразок ще не дає при розвантаженні залишкової деформації. Це точка В. Найбільше напруження, до якого залишкова деформація при розвантаженні не виявляється, називається границею пружності.
Границя пружності є характеристика, що не пов'язана із законом Гука. Точки А і В знаходяться дуже близько одна від одної і як правило, різницею між Далі іде перехід до горизонтальної площадки СД- це площадка текучості. На цій стадії подовження зразка зростає при сталому значенні розтягальної сили Рт. Такий процес деформації називається текучістю матеріалу, він супроводжується залишковим (пластичним) подовженням, яке зникає після розвантаження.
Границею текучості Далі (після стадії текучості) матеріал знову набирає здатності збільшувати опір деформуванню ДЕ- ділянка зміцнення. Точка Е відповідає найбілішому зусиллю Ртах яке може витримати зразок. Напруження, що відповідає максимальній силі Рмак називається тимчасовим опором, або границею міцності і позначається
Основними характеристика пружності і міцності матеріалів є границя пружності
Повне подовження зразка за границею пружності складається з двох частин: пружної і пластичної.
— пластична складова абсолютної деформації, не зникає.
— пружня складова - зникає при розвантаженні
Характеристики пластичності матеріалу 1.
- початкова довжин
2. Відносне звуження зразка після розриву
Робота деформації
Повна робота пружної деформації
Питома робота деформації
Питома робота деформації виражається площею трикутника на діаграмі Діаграму в координатах
Лекція № Зсув З деформацією зсуву ми зустрічаємося тоді, коли з 6 компонентів головного вектора та головного момента внутрішніх сил відмінні від 0 тільки поперечні сили
Запишемо вираз для Q:
(1), вважаючи що дотичні напруження розділені по площі поперечного перерізу
γ- кут зсуву, або відносний зсув
Залежність між навантаженням та деформацією зсуву можна простежити за діаграмою зсуву.
- границя пружності
Експериментально діаграму зсуву можна зняти при скручуванні труби. Між дотичним напруженням
Умова мiцності при зсуві (зрізі) може бути записана:
- діаметр болта.
Для болтових та заклепкових з'єднань проводять також розрахунок на зминання:
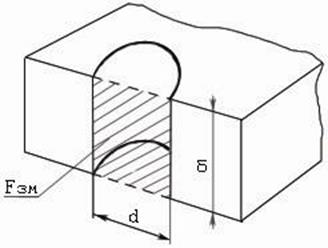
Fзм – площа зминання Fзм = δ∙d
σ зм = Р/Fзм = Р/δ∙d ≤ [σ зм] d ≥ Р/δ∙[σ зм] [σ зм] = (2-2,5) [σ] Для забезпечення умов міцності на зріз та зминання, треба з двох знайдених діаметрів взяти більший. Розрахунок зварних з'єднань
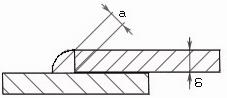
Якщо не враховувати наплива, то в перерізі кутовий шов має форму рівнобедренного прямокутного трикутника
a = δ∙cos45° = 0,78 Руйнування шва буде проходити по його мінімальному перерізу висотою a= 0,78. Розрахункова площа перерізу шва: Fe = a ∙ lт = 0,7∙δ∙l, де Fe – єлектрична дуга
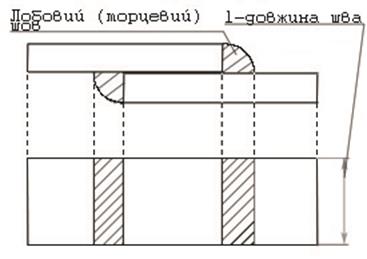
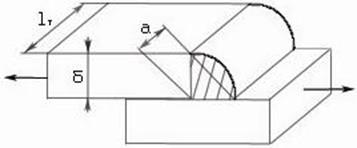
Для торцевого шва:
lт – розрахункова довжина торцевого шва Fе = a ∙ lт = 0,78∙lт Умова міцності шва: τ = P/Fe ≤ [τe] Якщо шва два: зверху і знизу, то:
Fe = 2∙a∙lт = 1,4∙δ∙lт тоді умова міцності τ = P/Fe = P/1,4∙δ∙lт ≤ [τe]
[τe] – табличне значення; [τe] = 80 МПа – для ручного зварювання електродами з тонкою обмазкою; [τe] = 100 Мпа – для автоматичного зварювання та ручного зварювання електродами з товстою обмазкою; Оскілбки на початку та в кінці шва внаслідок непровару його якість погіршується, дійсну його довжину збільшуємо порівняно з розрахунковою на 10мм, тобто: l = lт + 10мм де l дійсна довжина шва.
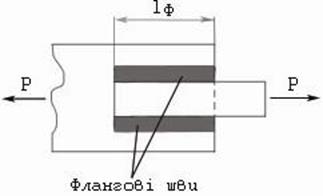
Для флангових швів:
Fe = a∙lф = 0,78∙(l – 10), так як їх ставлять паралельно, то: τ = P / 1,4∙δ∙(l – 10), 1,4 це 0,7∙2
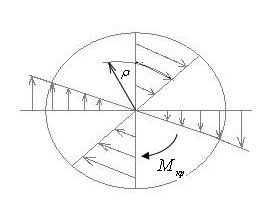
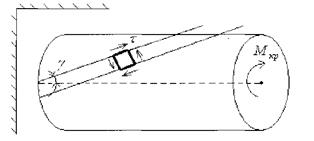
Допустимі напруження при зсуві: 2. За другою теорією міцності: τ = (0,7 ÷ 0,8) ∙ [σ]; τ ≤ [τ] 3. За третьою теорією міцності: τ ≤ [τ] [τ] = 0,5 ∙ [σ] 4. За четвертою теорією міцності: [τ] = 0,6 ∙ [σ] Лекція № Тема: „Кручення" Деформація кручення спричиняються парами сил, площини яких перпендикулярні до осі стержня. Тому при крученні з 6 основних факторів виникає тільки один - крутний момент Мкр. Стержні, які працюють на кручення звуться валами.
Під дією скручувального моменту, що прикладен на вільному кінці стержня будь яки переріз на відстані X від місця закріплення повертається відносно закріпленого перерізу на кут φ- кут закручування.
Мпу - момент до якого зберігається прямолінійна залежність між навантаженням та деформацією; МТ - момент, що відповідає початку текучості; Мв - крутний момент, який спричинює руйнування вала. Щоб визначити напруження у поперечних перерізах стержня розглянемо: 1. Статична сторона задачі
τ- дотичні напруження, яке діє на елементарній площадці dF, розташований на довільній відстані ρ від центра перерізу.
2. Геометрична сторона задачі Розглянемо відрізок вала довжиною
- кут зсуву на поверхні стержня.
Фізична сторона задачі Розглянемо елемент. Елемент перебуває в умовах чистого зсуву, тоді:
Максимальне напруження:
  Підставляючи в статичну сторону задачі вираз Підставляючи в статичну сторону задачі вираз 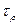 
кручення(одиниці виміру
Якщо вал трубчастий або полий тоді:
Для визначення взаємного кута закручування двох перерізів, розташованих на відстані l:
Визначимо дотичне напруження на відстані
    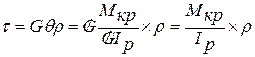
 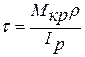 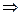 
Умова міцності при крученні
Лінійний напружений стан
Кут α – кут повороту вважаємо додатним, якщо він відраховується проти годинникової стрілки. На нахиленій площадці напруження паралельні осьовій силі N=P в перерізі
Проекціюючи
Максимальні дотичні напруження виникають при α=45º:
Правило знаків для дотичних напружень: дотичне напруження на площадці вважають додатним, якщо воно намагається повернути частину елемента, яка розглядається, відносно будь-якої точки, взятої всередині її за годинниковою стрілкою.
ЛЕКЦІЯ № Плоский напружений стан Плоский напружений стан виникає у випадку, коли два головних напруження не дорівнюють нулю, а третє дорівнює нулю. Нехай
Виділимо площадку α – переріз І-І, та β – переріз ІІ-ІІ. Переріз І-І провели під кутом β нормаль Напруження
Де З формул для лінійного напруженого стану:
знак
Використавши додавання остаточно знайдемо:
На площадці ІІ-ІІ проведем нормаль Тоді:
З цих рівнянь маємо, що:
Максимальне дотичне напруження:
В теорії плоско напруженого стану можна розмежувати дві основні задачі: пряма і зворотна.
Пряма задача. В точці відомі положення головних площадок, і відповідні до них головні напруження. Треба знайти нормальні і дотичні напруження, що діють на площадках, які нахилені під заданим кутом
Зворотна задача. В точці відомі нормалі й дотичні напруження, що діють у двох взаємно перпендикулярних площадках, що походять через дану точку. Треба знайти головні площадки та головні напруження.
Формули для обчислень:
Лекція №
ЛЕКЦІЯ №
Розтяг - стиск Розтяг або стиск стержня спричинюється силами, що діють уздовж його осі. У цьому випадку в поперечних перерізах стержня із шести внутрішніх силових факторів виникає лише один - поздовження (осьова сила
Для визначення сили Епюра - це графік (діаграма), яка показує як змінюється внутрішні зусилля при переході від перерізу до перерізу стержня. Правила побудови епюри: 1. Розбиваємо на ділянки. 2. Вісь (базу), на якій будується епюра, завжди вибирають так, щоб вона була паралельна або просто збігалась з віссю стержня. 3. Ординати на епюрі відкладають від осі епюра по перпендикуляру. 4. Штрихують епюри лініями, що перпендикулярні до бази. 5. Величини відкладають в певних масштабах
Поздовж сила вважається додатною, якщо вона спричинює розтяг, та від'ємною, якщо спричинює стискання. Наприклад:
Але можна визначати реакції Ra коли будемо йти з вільного кінця.
Розсічемо стержень довільним поперечним перерізом
Статична сторона задачі:
З цього рівняння не можна визначити напруження
Геометрична сторона задачі:
перерізи стержня плоскі до деформації, залишаються плоскими і після неї, переміщуючись поступово вздовж осі стержня (гіпотеза плоских перерізів)
подовжуються на одну і ту саму величину
і їхні відносні подовження
Фізична сторона задачі: полягає у встановленні залежності між деформаціями та напруженнями. При пружних деформаціях ця залежність лінійна і називається законом Гука.
Е - модуль пружності першого роду, або модуль Юнга. Це одна х фізичних констант матеріалу, виражається в Па Для однорідного та ізотропного матеріалу Е - стала величина тоді
Якщо Якщо Визначимо деформацію стержня
—з-н Гука для абсолютних подовжен
Добуток ЕГ називається жорсткістю поперечного перерізу стержня при розтягу - ділянці поздовжня сила та поперечний переріз змінні, то
Розглянемо поперечну деформацію стержня
-абсолютна поперечна деформація стержня
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
| Поделиться: |

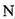 )
)
 необхідно побудувати її графік, або епюр.
необхідно побудувати її графік, або епюр.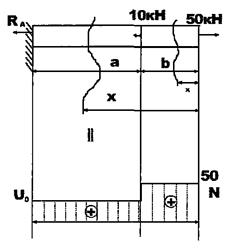
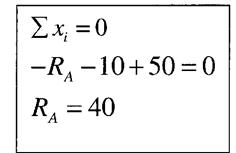

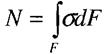
 , оскільки невідомий закон розподілу їх в точках поперечного перерізу
, оскільки невідомий закон розподілу їх в точках поперечного перерізу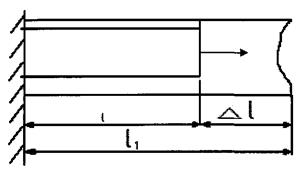 При деформації розтягу стержня поперечні
При деформації розтягу стержня поперечні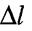 Таким чином всі волокна стержня
Таким чином всі волокна стержня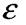 однакові
однакові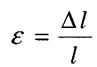
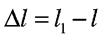
 - відносне подовження або деформація (величина безрозмірна)
- відносне подовження або деформація (величина безрозмірна)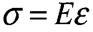
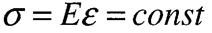
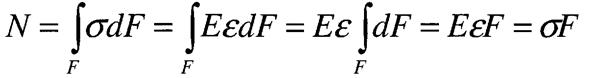
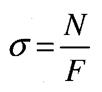
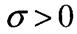 то це напруження розтягу
то це напруження розтягу то це напруження стиску
то це напруження стиску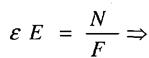
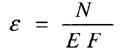
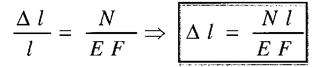
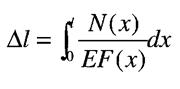
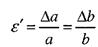
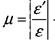
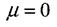
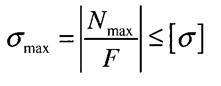
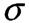 - допустиме напруження. При розтягу допустиме напруження позначають
- допустиме напруження. При розтягу допустиме напруження позначають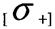 при стиску
при стиску 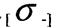
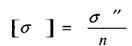
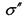 -небезпечне напруження
-небезпечне напруження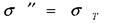
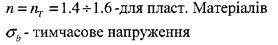
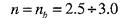
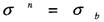 -для крихких матеріалів
-для крихких матеріалів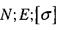 знайти:
знайти: 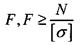
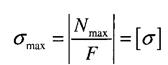
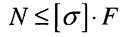
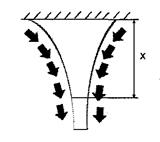
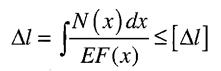 Іноді для забезпечення нормальної роботи машин та споруд розміри деталей треба вибрати так, щоб задовольнити умову жорсткості
Іноді для забезпечення нормальної роботи машин та споруд розміри деталей треба вибрати так, щоб задовольнити умову жорсткості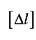
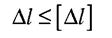 - допустиме значення зміни довжини
- допустиме значення зміни довжини
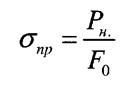
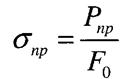
 пр і
пр і 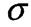 пц нехтують!!
пц нехтують!!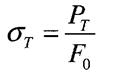
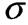 т зветься найменше напруження, при якому деформація зразка відбувається при сталому розтягальному зусиллі.
т зветься найменше напруження, при якому деформація зразка відбувається при сталому розтягальному зусиллі.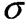 в
в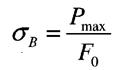
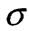 пр, границя текучості
пр, границя текучості  т, границя міцності(тимчасовий опір)
т, границя міцності(тимчасовий опір) 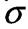 б
б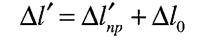
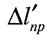
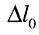
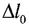 Відносне подовження після розриву
Відносне подовження після розриву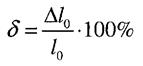
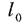 - приріст довжини після розриву
- приріст довжини після розриву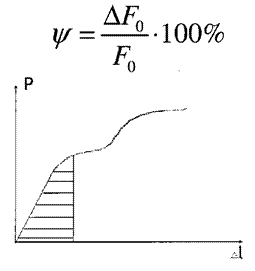

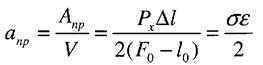
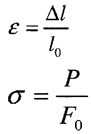
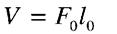
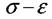 будують, щоб охарактеризувати тільки механічні характеристики матеріалу, тобто вид діаграми
будують, щоб охарактеризувати тільки механічні характеристики матеріалу, тобто вид діаграми 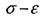 не залежить від розмірів зразка, та його площі поперечного перерізу.
не залежить від розмірів зразка, та його площі поперечного перерізу.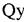 та
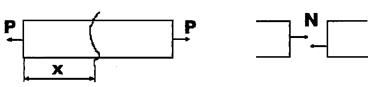
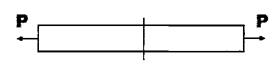
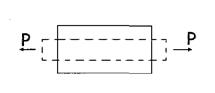
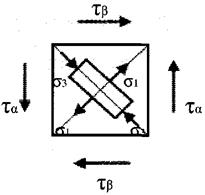
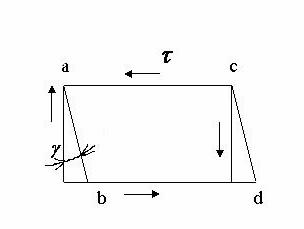
та 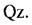 Деформацію зсуву можна получити тоді, коли, наприклад, на стержень з протилежнихбоків на дуже близької відстані одна від одноїді.ть 2 рівні сили, які перпендикулярні до осі бруса та спрямовані в протилежні сторони. Приклад: розріз ножницями полоси:
Деформацію зсуву можна получити тоді, коли, наприклад, на стержень з протилежнихбоків на дуже близької відстані одна від одноїді.ть 2 рівні сили, які перпендикулярні до осі бруса та спрямовані в протилежні сторони. Приклад: розріз ножницями полоси: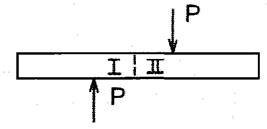
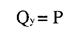
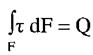
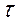 рівномірно
рівномірно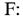 тоді
тоді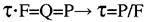
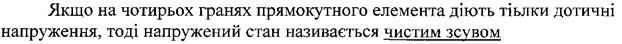
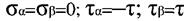
 Розглянемо деформаційний елемент:
Розглянемо деформаційний елемент:

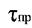
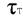
 - границя текучості
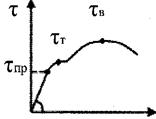
- границя текучості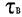 - границя міцності
- границя міцності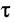 та кутом зсуву
та кутом зсуву 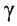 існує лінейна залежність:
існує лінейна залежність: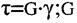 - коефіцієнт пропорційності, який називається модулем пружності
- коефіцієнт пропорційності, який називається модулем пружності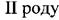
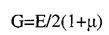
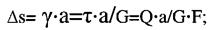
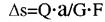 - закон Гука при зсуві
- закон Гука при зсуві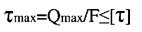
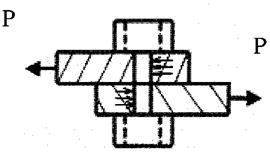 Якщо дотичні напруження розподіленні по перерізу рівномірно, матимемо
Якщо дотичні напруження розподіленні по перерізу рівномірно, матимемо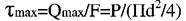
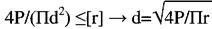

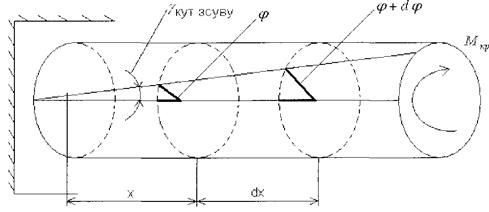
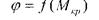 Залежність називаються діаграмами кручення, які
Залежність називаються діаграмами кручення, які визначають експериментально:
визначають експериментально:
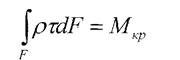
 виділений з розглядує мого вала.
виділений з розглядує мого вала.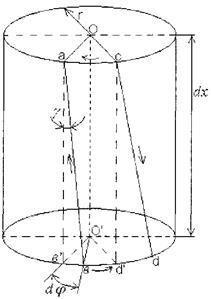
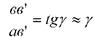
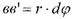

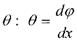
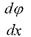
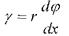
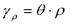
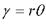
 - відносний кут закручування позначається через, одиниці виміру тоді. Якщо виділити на поверхні елемент радіуса ρ то
- відносний кут закручування позначається через, одиниці виміру тоді. Якщо виділити на поверхні елемент радіуса ρ то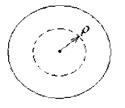
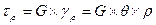
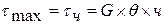
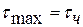
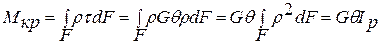 звідси:
звідси:
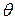 - відносний кут закручування
- відносний кут закручування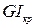 - жорсткість поперечного перерізу стержня
- жорсткість поперечного перерізу стержня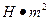 )
)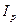 - полярний момент інерції.
- полярний момент інерції.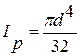 - для суцільного вала.
- для суцільного вала.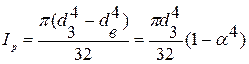 ;
; 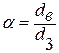 .
.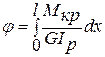
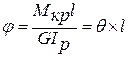
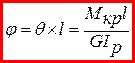 - закон Гука при крученні.
- закон Гука при крученні. :
: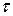
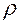
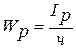
 - полярний момент опору при крученні.
- полярний момент опору при крученні.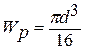 - для суцільного круглого вала.
- для суцільного круглого вала.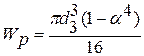 - для трубчастого перерізу.
- для трубчастого перерізу.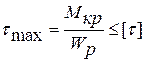
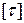 - допустиме напруження при крученні.
- допустиме напруження при крученні.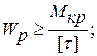
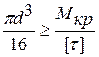
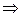
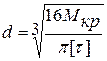
 В поперечних перерізах стержня нормальні напруження:
В поперечних перерізах стержня нормальні напруження:
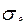
 На площадці, яка нахилена під кутом α, діють нормальні напруження та дотичні.
На площадці, яка нахилена під кутом α, діють нормальні напруження та дотичні. Площа поперечного перерізу стержня була
Площа поперечного перерізу стержня була  , після повороту площа площадки:
, після повороту площа площадки: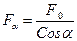
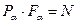

 на нормаль
на нормаль  до площадки і на площину перерізу, дістанемо:
до площадки і на площину перерізу, дістанемо:

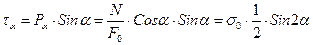

 ,
,  ,
, 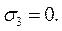
 Проведемо перерізи І-І, ІІ-ІІ, ІІІ-ІІІ, ІV-IV
Проведемо перерізи І-І, ІІ-ІІ, ІІІ-ІІІ, ІV-IV .Площадки (α) і (β) перпендикулярні.
.Площадки (α) і (β) перпендикулярні.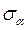 і
і  на площадці α будуть визиватись як дією
на площадці α будуть визиватись як дією  , так і дією
, так і дією  . Тоді застосовуючи принцип суперпозиції, тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів, можемо записати:
. Тоді застосовуючи принцип суперпозиції, тобто розглядаючи цей плоский напружений стан як накладання двох ортогональних одновісних напружених станів, можемо записати:

 і
і  -напруження, що спричинені дією
-напруження, що спричинені дією  ; а
; а  і
і  - напруження, що спричиняються дією
- напруження, що спричиняються дією  .
. ;
; 
 Для визначення
Для визначення 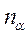 утворює з напруженням
утворює з напруженням  кут
кут  . Тоді
. Тоді 

 так як відрахунок ведеться за годинниковою стрілкою. Тоді
так як відрахунок ведеться за годинниковою стрілкою. Тоді ;
; 



 кут
кут  .
.
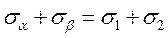 ─ сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від кута нахилу цих площадок і дорівнює сумі головних напружень.
─ сума нормальних напружень по двох взаємно перпендикулярних площадках не залежить від кута нахилу цих площадок і дорівнює сумі головних напружень. ─ ця рівність виражає закон парності дотичних напружень.
─ ця рівність виражає закон парності дотичних напружень. ,
,  .
. до головних;
до головних;






