
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Діаграма критичних напруженьСодержание книги
Поиск на нашем сайте
З формули для критичних напружень (8) видно, що в залежності від гнучкості
Звідки Тобто, нижня границя гнучкості стрижня, за якої можна застосовувати формулу Ейлера, становить а) область малих гнучкостей (для сталі Ст. 3 б) область середніх гнучкостей (для сталі Ст. 3
де коефіцієнти Для кожного матеріалу за різних значеннях Умова стійкості центрально стиснутого стрижня має вигляд
де
4. Проектний розрахунок стиснутих стрижнів на стійкість
де З урахуванням виразу (12) умова стійкості (11) набуває вигляду
Виходячи з умови стійкості, можна розв’язувати наступні типи задач:
а) перевіряти стійкість заданого стрижня, формула (13); б) Визначати допустиму стискальну силу за формулою
в) добирати необхідні розміри поперечних перерізів стиснутих стрижнів за формулою
Під час розв’язуванні задач останнього типу використовують метод послідовних наближень, оскільки у формулі (15) є дві невідомі – шукана площа поперечного перерізу
Приклад 1. Підібрати за сортаментом прокатної сталі і раціонально розмістити поперечний переріз стояка завдовжки Встановлюємо коефіцієнти зведеної довжини для обох головних площин: при згині відносно осі Оскільки Гнучкості стрижня виражаємо через невідомі поки що головні радіуси інерції: у площині
у площині
Потрібні розміри поперечного перерізу одного кутника підбираємо з умови стійкості (15) методом послідовних наближень. I наближення: Прийнявши
Рис. 6 Тут
З таблиці сортаменту (ГОСТ 8510 - 72) (дод. 1) добираємо кутник Визначимо головні радіуси інерції перерізу стояка:
де а – відстань між осями
Оскільки З таблиці коефіцієнтів для Методом лінійної інтерполяції для
II наближення: візьмемо значення коефіцієнту
Обчислюємо потрібну площу одного кутника
За таблицями сортаменту вибираємо кутник Максимальна гнучкість стрижня
Розміри поперечного перерізу, прийняті в другому наближенні є близькі до оптимальних. Виконуємо перевірку за напруженнями:
.Допускається перевантаження 5%. Перевіряємо стійкість стояка в площині Маємо: Стійкість в площині Перевіряємо коефіцієнт запасу стійкості стояка з вибраними розмірами поперечного перерізу. Оскільки За формулою (8) знаходимо:
Критична сила
Згідно з формулою (1) коефіцієнт запасу стійкості:
СПИСОК ЛІТЕРАТУРИ
1. Беляев Н. М. Сопротивление материалов. – М.: Физматгиз, 1962. 2. Сборник задач по сопротивлению материалов / Под ред. В. К. Качурина. – М.: Наука, 1970. 3. Ковтун В. В., Павлов В. С., Дорофеєв О. А. Опір матеріалів Розрахункові роботи. – Львів: Афіша, 2002. 4. Корнілов О. А. Опір матеріалів. – К.: ЛОГОС, 2000. 5. Сопротивление материалов / Под. ред. Н. А. Костенко. – М.: Высшая школа, 2000. 6. Писаренко Г. С., Квітка О. Л., Уманський Е. С. Опір матеріалів. – К.: Вища школа, 1993. 7. Посацький С. Л. Опір матеріалів. – Львів, 1973.
НАВЧАЛЬНЕ ВИДАННЯ КУРСОВА РОБОТА
|
||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 262; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.7.226 (0.01 с.) |

 , критичне напруження
, критичне напруження  може бути різним. Якщо гнучкість
може бути різним. Якщо гнучкість 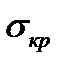 може набувати значень, що перевищують границю пропорційності матеріалу стрижня
може набувати значень, що перевищують границю пропорційності матеріалу стрижня 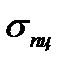 . Оскільки формула Ейлера і формула для визначення
. Оскільки формула Ейлера і формула для визначення  одержані за допущення, що стрижень під час втраті стійкості деформується пружно і матеріал знаходиться в межах закону Гука (тобто
одержані за допущення, що стрижень під час втраті стійкості деформується пружно і матеріал знаходиться в межах закону Гука (тобто  ), то величина критичних напружень повинна бути обмежена
), то величина критичних напружень повинна бути обмежена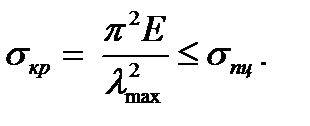
 (9)
(9) . Так, для сталі Ст. 3 з пружними характеристиками
. Так, для сталі Ст. 3 з пружними характеристиками 
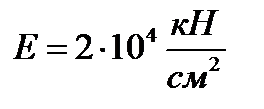 дістаємо
дістаємо 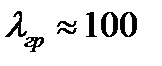 . Отже, для таких сталей формула Ейлера застосовна, якщо
. Отже, для таких сталей формула Ейлера застосовна, якщо  . Це – область стрижнів великої гнучкості. Область гнучкостей
. Це – область стрижнів великої гнучкості. Область гнучкостей  можна розділити на:
можна розділити на: ), за яких немає небезпеки втрати стійкості і стрижні слід перевіряти тільки на міцність. Якщо
), за яких немає небезпеки втрати стійкості і стрижні слід перевіряти тільки на міцність. Якщо 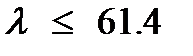 напруження
напруження  , де
, де  - границя текучості матеріалу стрижня;
- границя текучості матеріалу стрижня; ). Визначення критичних напружень в цій області викликає певні труднощі, оскільки матеріал в цьому випадку перебуває в пружнопластичному стані (
). Визначення критичних напружень в цій області викликає певні труднощі, оскільки матеріал в цьому випадку перебуває в пружнопластичному стані ( ). У інженерних розрахунках для визначення цих напружень застосовують формулу Ясинського, що одержана за результатами обробки експериментальних даних:
). У інженерних розрахунках для визначення цих напружень застосовують формулу Ясинського, що одержана за результатами обробки експериментальних даних: (10)
(10) , беруться з таблиць. Зокрема, для сталі Ст. 3
, беруться з таблиць. Зокрема, для сталі Ст. 3  . Для дерева (сосна)
. Для дерева (сосна) 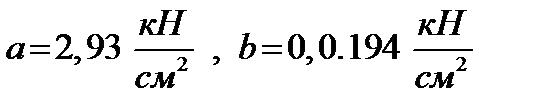 .
.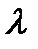 можна на основі наведених вище співвідношень побудувати графік залежності напруження
можна на основі наведених вище співвідношень побудувати графік залежності напруження  від гнучкості
від гнучкості  . Цей графік називається діаграмою критичних напружень. Для сталі Ст. 3 ця діаграма показана на рис. 4.
. Цей графік називається діаграмою критичних напружень. Для сталі Ст. 3 ця діаграма показана на рис. 4. (11)
(11) - допустиме напруження стійкості. Це напруження виражають через основне допустиме напруження на стиск
- допустиме напруження стійкості. Це напруження виражають через основне допустиме напруження на стиск  :
: (12)
(12)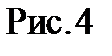
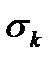


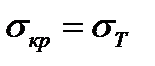




 - коефіцієнт поздовжнього згину (зменшення основного допустимого напруження стиску) (
- коефіцієнт поздовжнього згину (зменшення основного допустимого напруження стиску) ( ), що залежить від матеріалу та гнучкості
), що залежить від матеріалу та гнучкості  стрижня. Значення цього коефіцієнта беруться з таблиці.
стрижня. Значення цього коефіцієнта беруться з таблиці. (13)
(13) ; (14)
; (14) . (15)
. (15) , та коефіцієнт
, та коефіцієнт  . (Коефіцієнт
. (Коефіцієнт  . Якщо розміри поперечного перерізу невідомі, то невідомі і радіуси інерції перерізу “
. Якщо розміри поперечного перерізу невідомі, то невідомі і радіуси інерції перерізу “  “, а отже відповідно і гнучкість
“, а отже відповідно і гнучкість  та коефіцієнт
та коефіцієнт 











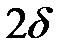






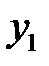

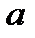
 З питанням добору розмірів поперечного перерізу центрально стиснутого стрижня тісно пов’язане питання раціональної форми поперечних перерізів. Небезпека втрати стійкості стиснутого стрижня тим менша, чим менша його найбільша гнучкість
З питанням добору розмірів поперечного перерізу центрально стиснутого стрижня тісно пов’язане питання раціональної форми поперечних перерізів. Небезпека втрати стійкості стиснутого стрижня тим менша, чим менша його найбільша гнучкість  , тобто чим більші, за фіксованого значення площі поперечного перерізу
, тобто чим більші, за фіксованого значення площі поперечного перерізу  , який складається з двох нерівнобоких кутників і стискається осьовою силою
, який складається з двох нерівнобоких кутників і стискається осьовою силою 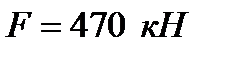 (рис. 5, а). Матеріал, з якого виготовлені кутники – сталь з допустимим напруженням на стиск
(рис. 5, а). Матеріал, з якого виготовлені кутники – сталь з допустимим напруженням на стиск  . Схема закріплення стояка показана на рис. 6, а. Розмір
. Схема закріплення стояка показана на рис. 6, а. Розмір 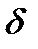 прийняти рівним товщині полички
прийняти рівним товщині полички  .
. (у площині
(у площині  )
)  ; при згині відносно осі
; при згині відносно осі  (у площина
(у площина 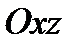 )
)  .
. , переріз необхідно розмістити так, щоб
, переріз необхідно розмістити так, щоб 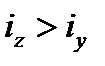 (рис. 5, б). У цьому разі значення критичної сили буде найбільшим.
(рис. 5, б). У цьому разі значення критичної сили буде найбільшим. (відносно осі
(відносно осі  )
) ;
; (відносно осі
(відносно осі  )
)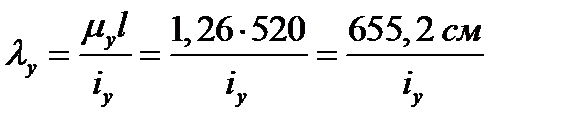 .
. , маємо:
, маємо: .
. - кількість кутників.
- кількість кутників.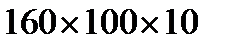 , для якого
, для якого  ,
,  ,
,  ,
,  ,
, 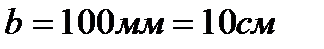 ,
,  .
. =5,13 см;
=5,13 см;  ;
; ,
, і
і 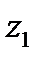 (рис. 6, б).
(рис. 6, б). см,
см,  ,
, 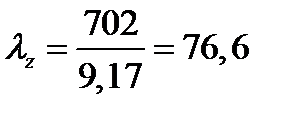 .
. підбір перерізу будемо здійснювати за гнучкістю у площині
підбір перерізу будемо здійснювати за гнучкістю у площині  , тобто
, тобто 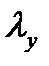 .
.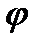 (табл. 1 дод. 2) для сталі Ст.3 маємо:
(табл. 1 дод. 2) для сталі Ст.3 маємо:
 , для
, для 
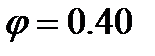 .
. знаходимо:
знаходимо: .
.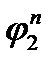 як середнє арифметичне початкового і кінцевого значень першого наближення
як середнє арифметичне початкового і кінцевого значень першого наближення .
. .
.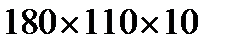 , для якого
, для якого  ,
, 
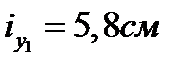 ,
,  ,
,  .
. і
і 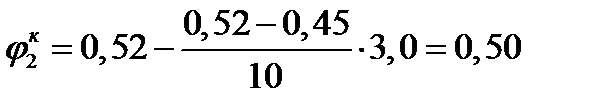 , що є близьке до значення
, що є близьке до значення  з точністю до двох знаків після коми. Різниця
з точністю до двох знаків після коми. Різниця  Обчислення припиняємо.
Обчислення припиняємо. .
. , за
, за 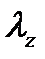 .
. і
і  .
. також забезпечена.
також забезпечена. , то до стояка можна застосувати формулу Ейлера.
, то до стояка можна застосувати формулу Ейлера. .
.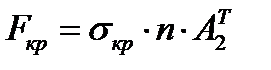 ;
;  .
. .
.


