
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Розрахунок балок на міцністьСодержание книги
Поиск на нашем сайте
При поперечному згині балки ( Нормальні напруження
де М(х) – згинальний момент в розглядуваному перерізів балки, значення якого беремо з епюри М(х); Iz – осьовий момент інерції перерізу відносно нейтральної осі
Із формули (2) випливає, що нормальні напруження по висоті балки змінюються за лінійним законом, їх епюра показана на рис. 5. У точках перерізу, найбільш віддалених від нейтральної осі
де Wz – осьовий момент опору перерізу. Моменти інерції Iz і моменти опору Wz обчислюються за такими формулами, зокрема: а) для прямокутного перерізу висотою h і шириною b
б) для круглого перерізу діаметром d
Моменти інерції та моменти опору прокатних профілів (двотавр, швелер) приведені у відповідних таблицях сортаментів.
Приклад розв'язання задачі Виконати розрахунок на міцність і жорсткість статично визначеної двотаврової балки (рис.7, а), модуль пружності матеріалу якої дорівнює 1. Визначити опорні реакції; 2. Побудувати епюру поперечних сил; 3. Побудувати епюру згинальних елементів; 4. Перевірити балку на міцність за найбільшими нормальними напруженнями, форма перерізу балки задається.
1. Визначення опорних реакцій. З умов рівноваги балки маємо:
Перевірка:
Значення та напрямки реакцій показані на рис. 6, а.
Рис. 6. Розрахункова схема балки (а) і епюри поперечних сил (б), згинальних моментів (в) та прогинів (г) 2. Побудова епюри поперечних сил. Для окремих ділянок балки знаходимо: а) ділянка І (0 ≤ х ≤ 1):
б) ділянка ІІ (1 ≤ х ≤ 3):
в) ділянка ІV (0 ≤ х ≤ 1):
г) ділянка ІІІ (1 ≤ х ≤ 3):
За обчисленими значеннями Q(x) будуємо епюру (див рис. 7, б).
3. Побудова епюри згинальних моментів. Для окремих ділянок маємо: а) ділянка І (0 ≤ х ≤ 1):
б) ділянка ІІ (1 ≤ х ≤ 3):
На цій ділянці поперечна сила змінює знак в точці
У характерних точках ділянки значення згинального моменту:
в) ділянка ІV (0 ≤ х ≤ 1):
г) ділянка ІІІ (1 ≤ х ≤ 3):
За обчисленими значеннями згинальних моментів будуємо епюру, яка зображена на рис. 7, в.
4. Перевірка міцності балки за найбільшими нормальними напруженнями. Для заданого перерізу згідно формули (10) будемо мати
Отже, необхідно визначити момент опору для заданого перерізу відносно осі z. Даний поперечний переріз (рис. 7) має вертикальну вісь симетрії і тому центр ваги буде лежати на цій осі. Розбиваємо даний переріз на три фігури: прямокутник (позначений на рисунку номером 2) розміром
Рис. 7
Площі отриманих фігур рівні:
Знайдемо координату
На рисунку показано положення центра ваги -
Перевірка правильності обчислення координати центра ваги фігури.
Визначення головних центральних моментів інерції:
Визначення радіусів інерції перерізу:
Визначення моментів опору перерізу. Відносно осі
Умова міцності виконується.
|
|||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 620; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.221.59.242 (0.01 с.) |

 ,
, 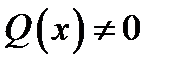 ) у її поперечних перерізах виникають нормальні та дотичні напруження.
) у її поперечних перерізах виникають нормальні та дотичні напруження. в довільній точці перерізу визначаються за формулою
в довільній точці перерізу визначаються за формулою , (2)
, (2)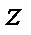 ;
;  – ордината точки перерізу, в якій визначається напруження. Знак нормальних напружень визначається у відповідності до дії згинального моменту.
– ордината точки перерізу, в якій визначається напруження. Знак нормальних напружень визначається у відповідності до дії згинального моменту.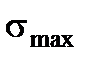
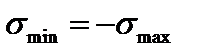


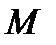

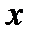

 , та в поперечному перерізі з найбільшим за абсолютною величиною згинальним моментом
, та в поперечному перерізі з найбільшим за абсолютною величиною згинальним моментом  виникають найбільші нормальні напруження
виникають найбільші нормальні напруження , (3)
, (3)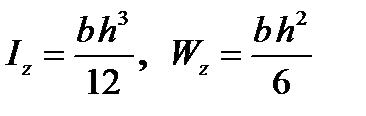 ; (4)
; (4) . (5)
. (5) , допустиме напруження взяти [
, допустиме напруження взяти [ 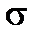 ]=160 МПа. В ході розрахунку виконати наступне:
]=160 МПа. В ході розрахунку виконати наступне:

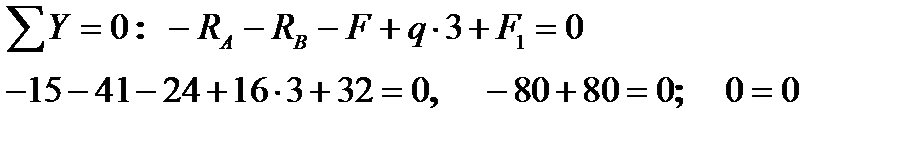
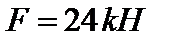









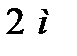





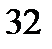












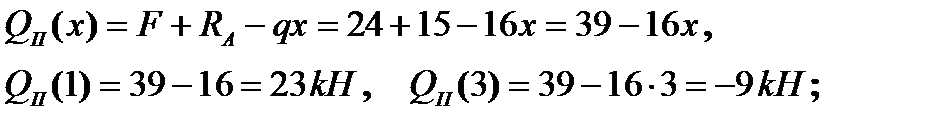




 де поперечна сила
де поперечна сила  . У цій точці згинальний момент набуває екстремального значення:
. У цій точці згинальний момент набуває екстремального значення: .
.
 ;
;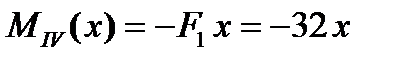 ,
, ;
; ,
, .
. .
. см, та два прямокутних трикутники (позначені на рисунку номерами 1 та 3), симетрично розташовані відносно осі симетрії перерізу. Виберемо базову систему координат наступним чином: вісь
см, та два прямокутних трикутники (позначені на рисунку номерами 1 та 3), симетрично розташовані відносно осі симетрії перерізу. Виберемо базову систему координат наступним чином: вісь  співпадає з віссю симетрії перерізу, а вісь
співпадає з віссю симетрії перерізу, а вісь  - горизонтальна і проходить через найнижчу точку перерізу.
- горизонтальна і проходить через найнижчу точку перерізу. ;
; .
. Визначимо відносно базової системи координат положення центра ваги поперечного перерізу. Для цього визначимо координати центрів ваги фігур відносно базової системи координат:
Визначимо відносно базової системи координат положення центра ваги поперечного перерізу. Для цього визначимо координати центрів ваги фігур відносно базової системи координат: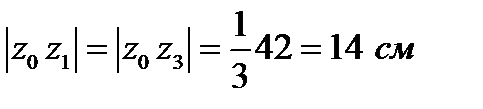 ;
; .
. :
: .
. . Виберемо в цій точці центральну систему координат
. Виберемо в цій точці центральну систему координат  . Ця система координат є головною, оскільки вісь
. Ця система координат є головною, оскільки вісь  співпадає з віссю симетрії. Обчислимо координати центрів ваги всіх трьох частин фігури відносно цієї системи координат.
співпадає з віссю симетрії. Обчислимо координати центрів ваги всіх трьох частин фігури відносно цієї системи координат. ;
;  ;
;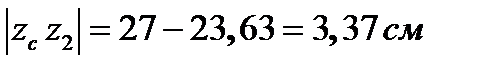 ;
;  .
.
 .
. ;
; ;
; ;
;

 :
:  . Найбільш віддаленими точками перерізу від осі
. Найбільш віддаленими точками перерізу від осі  є точки нижньої кромки перерізу. Тому
є точки нижньої кромки перерізу. Тому  .ю Таким чином:
.ю Таким чином: .
.



