
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Задача 3. Розрахунок статично визначних балок при прямому згиніСодержание книги
Поиск на нашем сайте
Умова задачі Виконати розрахунок статично визначеної балки на міцність, вибравши схему і переріз балки балки (рис. 1, 2) і числові дані згідно з завданням (таб. 1.). Матеріал балки – Ст. 3, модуль пружності якого Е =2·105 МПа. Допустиме напруження прийняти рівним [σ]=160 МПа. У ході розрахунку виконати наступне. 1. Зобразити схему балки у масштабі, позначити розміри її ділянок (в м) і нанести числові значення навантажень. 2. Визначити опорні реакції. 3. Побудувати епюри поперечних сил і згинальних моментів. 4. Перевірити балку на міцність за найбільшими нормальними напруженнями, форма перерізу балки задається. Т а б л и ц я 1 Числові значення геометричних параметрів і складових навантажень балки
Рис. 1.
Рис. 1
Основні теоретичні відомості Основні поняття. Поперечні сили та згинальні моменти Стрижень з прямою віссю, що працює на згин, називається балкою. Згин балки викликається зосередженими, розподіленими навантаженнями, а також зовнішніми моментами, які діють у площині, що проходить через вісь балки. Характерною ознакою деформації згину балки є зміна кривини її осі. Площина, в якій діють навантаження, називається силовою площиною.
Рис. 3. Навантаження, що діють на балку при прямому згині Якщо викривлена вісь балки лежить в силовій площині (рис. 3), то має місце прямий згин балки. При прямому згині скривлена вісь балки є плоскою кривою, що є геометричним місцем вертикальних переміщень точок осі балки. Ці переміщення називаються прогинами балки. При прямому згині в поперечних перерізах балки виникають дві внутрішні сили: поперечна сила
Рис. 4. Поперечні сили та згинальні моменти при прямому згині балки Внутрішні сили в довільному перерізі балки (рис. 4, а), яка знаходиться під дією зрівноваженої системи сил, визначаються таким чином: · поперечна сила Q(x) чисельно дорівнює алгебраїчній сумі проекцій на вісь · згинальний момент М(х) чисельно дорівнює алгебраїчній сумі моментів відносно осі На підставі одержаних формул (чи значень для характерних точок осі балки) для поперечних сил Q(x) та згинальних моментів М(х) будують їх епюри. Між згинальним моментом М(х), поперечною силою Q(x) та інтенсивністю розподіленого навантаження q (x) існують такі диференціальні залежності
Із цих залежностей випливають такі висновки:
1. На ділянках балки, де відсутнє розподілене навантаження ( 2. На ділянках балки, де діє рівномірно розподілене навантаження ( 3. На ділянках балки, де поперечна сила 4. У перерізі балки, в якому поперечна сила 5. На ділянці балки, на якій поперечна сила 6. У перерізі балки, в якому діє зосереджена сила, епюра Q(x) має стрибок на величину прикладеної сили, а епюра М(х) має злом в сторону дії цієї сили. 7. У перерізі балки, в якому діє зосереджений момент, епюра М(х) має стрибок на величину моменту пари сил.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 454; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.26.164 (0.009 с.) |

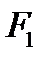 ,
, 
 ,
, 
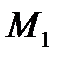 ,
, 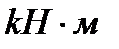
 ,
, 
 ,
, 
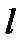 ,
, 
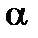

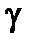




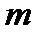
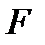

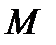
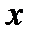

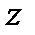
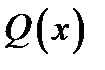 та згинальний момент
та згинальний момент  (рис. 4, а), для визначення яких використовується метод перерізів. Якщо обидва зазначені силові фактори
(рис. 4, а), для визначення яких використовується метод перерізів. Якщо обидва зазначені силові фактори  та
та  є відмінними від нуля, то такий згин називається поперечним. У випадку відсутності поперечних сил згин називається чистим.
є відмінними від нуля, то такий згин називається поперечним. У випадку відсутності поперечних сил згин називається чистим.

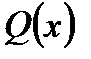
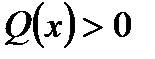
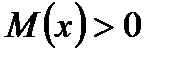
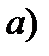

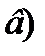
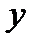 перерізу усіх зовнішніх сил, розташованих по один бік від цього перерізу. Додатними вважаються поперечні сили, які намагаються повернути розглядувану частину балки за ходом стрілки годинника (рис. 4, б);
перерізу усіх зовнішніх сил, розташованих по один бік від цього перерізу. Додатними вважаються поперечні сили, які намагаються повернути розглядувану частину балки за ходом стрілки годинника (рис. 4, б);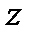 перерізу всіх зовнішніх сил, розташованих по один бік від цього перерізу. Додатними вважаються згинальні моменти від дії тих сил, що викликають розтяг нижніх волокон балки (рис. 4, в).
перерізу всіх зовнішніх сил, розташованих по один бік від цього перерізу. Додатними вважаються згинальні моменти від дії тих сил, що викликають розтяг нижніх волокон балки (рис. 4, в).
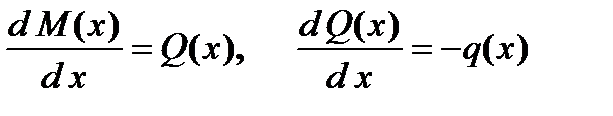 . (1)
. (1) ), поперечна сила Q(x) – постійна величина, а згинальний момент М(x) змінюється за лінійним законом.
), поперечна сила Q(x) – постійна величина, а згинальний момент М(x) змінюється за лінійним законом.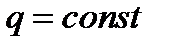 ), поперечна сила Q(x) змінюється за лінійним законом, а згинальний момент М(x) – за законом квадратної параболи, ввігнутої в сторону дії навантаження
), поперечна сила Q(x) змінюється за лінійним законом, а згинальний момент М(x) – за законом квадратної параболи, ввігнутої в сторону дії навантаження 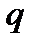 .
.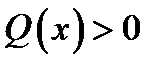 , згинальний момент М(x) зростає, а при
, згинальний момент М(x) зростає, а при 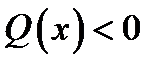 – М(x) спадає.
– М(x) спадає. , згинальний момент М(х) набуває екстремального (максимального чи мінімального) значення.
, згинальний момент М(х) набуває екстремального (максимального чи мінімального) значення. , згинальний момент
, згинальний момент 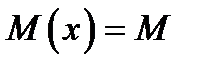 – постійна величина і на цій ділянці має місце чистий згин.
– постійна величина і на цій ділянці має місце чистий згин.


