Регулярные и нерегулярные выражения.

Трехпроходный транслятор.

Блок сканирования считывает исходную программу и представляет ее в форме файла лексем. Синтаксический анализатор читает этот файл и выдает новое представление программы, например, в постфиксной форме. Наконец, этот файл считывается генератором кода, который создает объектный код программы. Компилятор такого вида называется трехпроходным (рис. 1.1), так как программа считывается трижды (исходный текст программы, файл лексем и файл в постфиксной форме). Недостаток: Невысокая скорость выполнения, так как в большинстве вычислительных систем операции, связанные с обращением к файлам, осуществляются сравнительно медленно. Преимущества: Относительная независимость каждой фазы компилирования. Так как связь между обрабатывающими блоками осуществляется только через файлы данных, любой проход может быть реализован независимо от остальных. Это обеспечивает: 1. Возможность автономной разработки различных блоков компилятора разными разработчиками, необходимо только согласовать форматы промежуточных файлов. 2. Гибкость компилятора. Например, для реализации одного и того же языка для различных типов компьютеров, возможно использовать одни и те же блоки сканирования и синтаксического анализа, но написать специальные генераторы кода для каждого типа компьютера. При реализации семейства компиляторов с различных языков для одного типа компьютеров, очевидно, потребуются различные блоки сканирования и синтаксического анализа, но возможно использование общего генератора кода. 3. Минимальные требования к объему оперативной памяти (модули различных фаз компиляции можно загружать по очереди, выгружая при этом предыдущий).
	Для достижения высокой скорости компиляции применяется компилятор с однопроходной структурой. Для повышения эффективности выполнения объектной программы в процесс компилирования может включаться фаза оптимизации. Блок оптимизации легко встраивается в трехпроходный компилятор, где размещается, обычно, между синтаксическим анализатором и генератором кода. На этой фазе постфиксный файл используется в качестве входных данных и создается новый файл, содержащий постфиксную запись эквивалентной программы с улучшенными характеристиками. Поскольку блок оптимизации записывает свои входные данные в формате постфиксного файла, генератор кода не нуждается в изменении. На практике возможность оптимизации предусматривается по желанию пользователя:если необходимо, чтобы время компилирования было небольшим, блок оптимизации игнорируется;если же требуется получить программу с высокой скоростью выполнения, то после работы синтаксического анализатора вызывается блок оптимизации
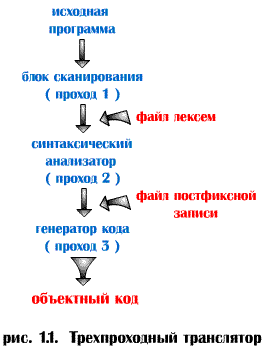
Однопроходный транслятор. Для достижения высокой скорости компиляции применяется компилятор с однопроходной структурой (рис. 1.2). На рисунке связи по управлению показаны обычными стрелками, передача данных - пунктирными. В этом случае синтаксический анализатор выступает в роли основной управляющей программы, вызывая блок сканирования и генератор кода, организованные в виде подпрограмм. Синтаксический анализатор постоянно обращается к блоку сканирования, получая от него лексему за лексемой из просматриваемой программы, до тех пор, пока не построит новый элемент постфиксной записи, после чего он обращается к генератору кода, который создает объектный код для этого фрагмента программы. Преимущество: Максимальная эффективность и скорость выполнения, так как программа рассматривается лишь однажды, количество операций обращения к файлам минимально (только чтение из исходного и запись в объектный файлы). Недостатки: 1.Проблемы при организации переходов вперед. Например, во время обработки предложения GOTO метка; могут встретиться трудности, так как "метка" еще не встречалась в тексте программы. 2.Неоптимальность создаваемой объектной программы. Например, если встречается текст:A=(B+C);P=(B+C)+(E+M);компилятор мог бы построить более эффективный объектный код, трансформировав программу следующим образом: A=(B+C);P=A+(E+M);Однако однопроходный компилятор может утратить часть нужной информации к тому времени, когда в тексте встретится формула (E+M). 3. Поскольку однопроходный компилятор должен полностью размещаться в памяти, его реализация сопровождается повышенными требованиями к ресурсу памяти, которые не всегда можно удовлетворить, имея систему с ограниченным объемом памяти.

Двухпроходный транслятор

Возможны и другие способы структурной организации компилятора. На рис. 1.3 показана структура двухпроходного компилятора, занимающая промежуточное положение между трехпроходным и однопроходным вариантами организации. В этом случае синтаксический анализатор, вызывая блок сканирования, получает лексему за лексемой и строит файлпостфиксной записи программы. Генератор кода считывает этот файл и создает объектный код программы. Подобной структуре свойственно относительно небольшое время выполнения, так как программа считывается лишь дважды (исходный текст и постфиксная запись). В этом случае легко разрешается проблема с оператором перехода вперед на метку, так как эта метка считывается на фазе первого прохода, перед вызовом генератором кода. В такой компилятор при необходимости легко включить блок оптимизации.

Интерпретатор

Интерпретаторы реализуют принцип, альтернативный компилированию. Компиляторы и интерпретаторы имеют много общего. Интерпретатор, тоже вначале просматривает исходную программу и выделяет в ней лексемы. Для этого используются блоки сканирования и анализаторы, аналогичные тем, которые входят в состав компилирующих программ. Однако интерпретатор вместо построения объектного кода, способного выполнять те или иные операции, сам производит соответствующие действия.

Достоинства интерпретатора:

· относительная простота реализации;

· удобство отладки програм;

Достоинства компилятора:

· скорость выполнения;

· независимость выполняемого кода от системы программирования;

· возможность передавать программы заказчикам без исходных текстов.

Большинство современных интерпретаторов выполняют не исходный код, а преобразуют его в промежуточный, который затем интерпретируется. Это позволяет несколько повысить скорость исполнения и избежать передачи заказчикам исходных текстов. Для трансляции классических языков программирования (C, C++, Паскаль, Delphi и др.) обычно используются компиляторы. Как интерпретаторы выполнены большинство реализаций Бейсика и языков управления СУБД. Язык сетевого программирования Java реализован как интерпретируемый специальной виртуальной Java-машиной. Это обеспечивает возможность исполнения промежуточного кода Java на любом типе компьютера, где имеется такая виртуальная Java-машина.

 

"Кросс-компиляторы" и конверторы

Поскольку компилятор преобразует исходную программу в совокупность битов, полученную строку битов можно использовать и на другой машине. Так как подготовка программы для одного типа ЭВМ осуществляется с помощью ЭВМ другого типа, соответствующие компиляторы получили название " кроссовых " (т.е. перекрестных).

Конвертор – это транслятор с одного языка на другой язык того же уровня. Примером конвертора может быть программа, преобразующая код на языке Паскаль в код на С, или данные об объекте проектирования во внутреннем формате одной САПР в формат другой САПР.

Определение языка

Прежде чем приступить к созданию компилятора, необходимо иметь четкое и однозначное определение исходного языка.

Можно представить язык состоящим из ряда строк (последовательностей символов). В описании языка определяется, какие строки принадлежат этому языку (синтаксис языка), и значение этих строк (семантика языка).

Синтаксис языка

Синтаксис – множество правил, которые задают множество формально правильных предложений. Синтаксис для конечного языка (состоящего из конечного числа строк) можно специфицировать, задав список строк.

Строки, принадлежащие языку, обычно называются предложениями языка. В реальных языках – бесконечное число предложений, так что их синтаксис нельзя определит путем перечисления этих предложений. Синтаксис очень простого языка можно описать на естественном языке, например – "все строки, состоящие только из 1 и 0" тогда 1111 и 1000110 – принадлежат языку, а 1020 – нет. Однако естественным языкам свойственны неоднозначности, поэтому для спецификации синтаксиса более сложных языков применяется более формальный метод определения синтаксиса.

Рассмотрим, например, предложение "Кошки спят". Слово "кошки" – подлежащее, а "спят" – сказуемое. Это предложение принадлежит языку, который можно описать, например, при помощи следующих синтаксических правил:

<предложение>::= <подлежащее><сказуемое>

<подлежащее>::= кошки | собаки

<сказуемое>::= едят | спят

Смысл этих трех строк таков: предложение состоит из подлежащего, за которым следует сказуемое. Подлежащее состоит либо из одного слова "кошки", либо из одного слова "собаки". Сказуемое состоит либо из слова "спят", либо из слова "едят".

Идея заключается в том, что любое предложение можно получить из начального символа <предложение> последовательным применением правил подстановки.

Формализм, или нотация, использованный при написании этих правил, называется Бэкуса–Наура формой (БНФ). синтаксические единицы <предложение>, <подлежащее> и <сказуемое> называются нетерминальными символами, слова "кошки", "собаки", "спят", "едят" – терминальными символами, а правила – порождающими правилами. Символы “::=”, “|”, а также скобки нетерминальных символов “<>” – это метасимволы языка БНФ (метасимволы не принадлежат описываемому языку, а относятся к языку описания.

Для рассмотрения задачи спецификации синтаксиса дадим несколько определений.

Алфавит – множество символов. Например: Русские буквы, Латинские буквы, цифры.

Если A – алфавит, A* (замыкание A) обозначает множество всех строк (включая пустую строку), составленных из символов, входящих в A. A+ обозначает множество всех строк (исключая пустую строку), состоящих из символов, входящих в A. Пустая строка обычно обозначается с помощью ε (эпсилон).

Синтаксис языка можно определить, пользуясь системой изображения множеств, например L = { 0 ⁿ 1 ⁿ | n ³ 0}. Данный язык включает строки, состоящие из одного или более нулей и того же числа последующих единиц, а также пустую строку.

Более сложный синтаксис языка лучше определять с помощью грамматики. В грамматику входит набор правил для получения предложений языка. Возьмем синтаксис L и воспользуемся следующими правилами:

1. S ® 0S1

2. S ® ε

Чтобы вывести предложение этого языка, поступим следующим образом. Начнем с символа S и заменим его на 0 S 1 или ε. Если S опять появился в полученной строке, его опять можно заменить с помощью одного из этих правил, и т.д. Полученная таким образом любая строка, не содержащая S, является предложением этого языка. Например,

S Þ 0S1 Þ 00S11 Þ 000S111 Þ 000111

Последовательность таких шагов называется выводом строки 000111, а символ Þ служит для разделения шагов вывода. Все предложения данного языка можно вывести, руководствуясь двумя правилами, любая строка, которую нельзя вывести с их помощью, не является предложением этого языка. Грамматику часто называют системой перезаписи.

Семантика языка.

 

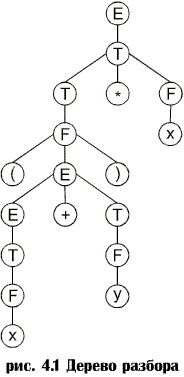
Семантика задает значение всем предложениям языка. Изменим пример про животных:

<предложение>::=<подлежащее><сказуемое>

<подлежащее>::= люди | собаки

<сказуемое>::= говорят | спят

Методы формального описания семантики разработаны недостаточно хорошо и в этих целях часто используется естественный язык.

Грамматика языка

Грамматика определяется как четверка (Vt, Vn, P, S), где Vt – алфавит, символы которого называется терминальными (терминалами), из них строятся цепочки порождаемые грамматикой. Vn – алфавит, символы которого называется нетерминальными (нетерминалами), используются при построении цепочек; они могут входить в промежуточные цепочки, но не должны входить в результат порождения. Vt и Vn не имеют общих символов, т.е. Vt ÇVn = Ø, полный алфавит (словарь) грамматики V определяется как Vt È Vn. P – набор порождающих правил, каждый элемент которых состоит из пары (α, β), где α находится в V+, а β в V*. α – левая часть правила, а β – правая, т.е. цепочки, построенные из букв алфавита V. Правило записывается α ® β.

S принадлежит Vn и называется начальным символом (аксиомой). Этот символ – отправная точка в получении любого предложения языка.

Грамматикой, генерирующей язык L = { 0 ⁿ 1 ⁿ | n ³ 0} является G ₀ = ({0,1}, { S }, P, S), где P = { S ® 0 S 1, S ® ε }.

Грамматикой, генерирующей язык L = { a ⁿ b ^m | n, m ³ 0} является G ₀ = ({ a, b }, { S, A, B }, P, S), где P = { S ® AB, A ® aA,
A ® ε, B ® bB, B ® ε }

Начав с символа S и применяя последовательно по одному из правил замены нетерминала в выводимой строке можно, например, генерировать строку aaabb:

S Þ AB Þ aAB Þ aaAB Þ aaaAB Þ aaaB Þ aaabB Þ aaabbB Þ aaabb

Каждая строка, которую можно вывести из начального символа, называется сентенциальной формой. Предложение – сентенциальная форма, содержащая только терминалы. Терминалы будем обозначать строчными (маленькими) буквами, а нетерминалы – прописными (большими).

Как правило, предложения языка можно генерировать с помощью более чем одной грамматики. Две грамматики, генерирующие один и тот же язык, называют эквивалентными. С точки зрения разработчика транслятора одна грамматика может быть гораздо удобней другой.

Иерархия Хомского.

Ограничение типов правил, которые могут появляться в грамматике позволяет определить ряд специальных классов грамматик. Одна из стандартных классификаций известна как иерархия Хомского. Ее описывают следующим образом:

1. Любая грамматика определенного ранее вида – грамматика типа 0.

2. Если для всех правил вида α ® β, |α| ® |β|, где | α | и | β | – длина, т.е. число символов соответственно α и β, то грамматика называется грамматикой типа 1, или контекстно-зависимой (КЗ).

3. Если все левые части правил грамматики состоят из одного нетерминального символа, то это грамматика типа 2, или контекстно-свободная (КС).

4. Грамматика называется грамматикой типа 3, или регулярной, если каждое правило грамматики имеют одну из следующих форм.

В случае грамматики, выровненной вправо, в правой части грамматики имеется не более одного нетерминала, который может быть только самым правым символом:

A ® a

A ® aB

B случае грамматики, выровненной влево, в правой части грамматики имеется не более одного нетерминала, который может быть только самым левым символом:

A ® a

A ® Ba

Иерархия – включающая, т.е. все грамматики типа 3 являются грамматиками типа 2 и т.д. Иерархия грамматик соответствует иерархии языков. Например, если язык можно генерировать с помощью грамматики типа 2, то его называют языком типа 2. Необходимо помнить, что если для генерации языка можно использовать несколько грамматик, то тип языка соответствует грамматике с наибольшим типом.

Иерархия Хомского важна с точки зрения построения трансляторов с различных языков. Чем меньше ограничений в грамматике, тем сложнее ограничения, которые можно наложить на генерируемый язык. Чем более универсален класс используемой грамматики, тем больше свойств языка мы можем описать. Однако чем более универсальна грамматика, тем сложнее должна быть программа, распознающая строки соответствующего языка.

Грамматики типа 3 можно использовать для описания некоторых свойств языков программирования или высокоуровневых языков описания аппаратуры. Например, для генерирования идентификаторов по определению многих языков программирования можно воспользоваться следующими правилами:

I ® l

I ® l R

R ® l

R ® d

R ® l R

R ® d R

где буква (l) и цифра (d) обозначают терминалы (для краткости будем считать так, потому что перечисление всех возможных букв и цифр потребовало бы написания слишком большого числа правил). Иногда удобно объединять правые части правил, имеющих одинаковые левые части. Вышеприведенную грамматику можно также записать в виде:

I ® l | l R

R ® l | d | l R | d R

Вертикальную черту здесь надо понимать как "или".

Многие "локальные" средства языков программирования, например константы, ключевые слова языка и строки, представляются с помощью грамматик типа 3. Некоторые очень простые языки описания аппаратуры также можно описать с помощью регулярной грамматики. Однако грамматики типа 3 генерируют только строго ограниченные типы языков –регулярные выражения.

Проблема разбора.

Компилятор должен решить проблему проверки строк символов, чтобы определить, принадлежат ли они данному языку, и если да, то распознать структуру строк в терминах порождающих правил грамматики. Эта проблема известна какпроблема разбора. Исследуем грамматику с порождающими правилами (E - начальный символ).

1. Е ® Е + Т

2. Е ® T

3. T ® T * F

4. T ® F

5. F ® (Е)

6. F ® x

7. F ® y

Ясно, что строка (x + y) * x принадлежит данному языку. В частности, это можно вывести следующим образом (для каждого шага вывода указан номер применяемого правила):

2) E Þ T

3) Þ T * F

4)) Þ F * F

5) Þ (E)* F

1) Þ (E + T) * F

2) Þ (T + T) * F

4) Þ (F + T) * F

6) Þ (x + T)*F

4) Þ (x + F) * F

7) Þ (x + y) * F

6) Þ (x + y) * x

Или же это можно вывести так:

2) E Þ T

3) Þ T * F

6) Þ T * x

4) Þ F * x

5) Þ (E) * x

1) Þ (E + T) * x

4) Þ (E + F) * x

7) Þ (E + y) * x

2) Þ (T + y) * x

4) Þ (F + y) * x

6) Þ (x + y) * x

На каждом этапе первого вывода самый левый нетерминал в сентенциальной форме замещался с помощью одного из порождающих правил грамматики. Поэтому данный вывод называется левосторонним. Второй вывод, на каждом этапе которого замещается самый правый нетерминал, называется правосторонним. Существуют также другие выводы, не являющиеся ни лево-, ни правосторонними, однако при реализации трансляторов они практически не используются.

Проблему разбора можно свести к

1) нахождению левостороннего разбора;

2) нахождению правостороннего разбора;

3) построению синтаксического дерева.

Дерево разбора.

Дерево разбора. Вывод может быть описан также в терминах построения дерева, известного как синтаксическое дерево (или дерево разбора). В случае со строкой

(x + y) * x

синтаксическое дерево будет таким, как показано на рис. 4.1.

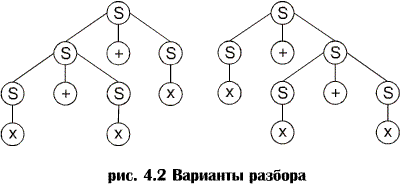
Неоднозначные грамматики.

Неоднозначные грамматики. В большинстве случаев левосторонний и правосторонний разборы и синтаксическое дерево являются уникальными. Однако для грамматики с порождающими правилами:

S ® S+S | x

предложение x + x + x имеет два синтаксических дерева (рис. 4.2) и два левосторонних (и правосторонних) разбора:

 

 

S Þ S + S	S Þ S + S
Þ S + S + S	Þ x + S
Þ x + S + S	Þ x + S + S
Þ x + x + S	Þ x + x + S
Þ x + x + x	Þ x + x + x

Если какое-либо предложение, генерированное грамматикой, имеет более одного дерева разбора, о такой грамматике говорят, что она неоднозначна. Эквивалентное условие заключается в том, что предложение должно иметь более одного левостороннего или правостороннего разбора. Задача установления неоднозначности грамматики является, в общем случае, неразрешимой, т.е. не существует универсального алгоритма, который принимал бы на входе любую грамматику и определял бы, однозначна она или нет. Некоторые неоднозначные грамматики можно преобразовать в однозначные, генерирующие тот же язык. Например, грамматика с порождающими правилами

S ® x | S + x

является однозначной и генерирует тот же язык, что и рассмотренная ранее неоднозначная грамматика.

Методы разбора обычно бывают нисходящими, т.е. начинают с начального символа и идут к предложению, или восходящими, т.е. начинают с предложения и идут к начальному символу.

Отказ от решения в разборе называют возвратом. Методы разбора могут быть недетерминированными и детерминированными в зависимости от того, возможен возврат или нет. Недетерминированные методы разбора весьма дорогие с точки зрения памяти и времени и крайне затрудняют включение в синтаксический разбор анализатор действий, выполняемых во время компиляции, результаты которых позднее должны быть аннулированы (например, построение таблицы символов и т.п.). В дальнейшем мы будем рассматривать лишь детерминированные методы разбора. Основное внимание в настоящем учебном пособии уделено методам нисходящего разбора, они же используются в лабораторных работах и при курсовом проектировании. Методы восходящего разбора рассмотрены в отдельной главе.

Пример структуры программы сканирования.

Пусть реализуемый язык состоит только из оператора присваивания БНФ языка:

<Присваивание>::= <Идент> = <Выражение>

Правило показывает, что в левой части присваивания – идентификатор, далее следует символ присваивания (=), справа – выражение;

<Выражение>::= <Операнд> | <Операнд> <Бин.оп> <Выражение>

Выражение – это операнд, или операнд, за которым следует бинарная операция и выражение;

<Бин.оп>::= "-" | "+" | "*" | "/"

Бинарная операция – символ арифметической операции " - ", " + "," * " или "/";

<Операнд>::= <Идент> | <Const>

Операнд – это идентификатор или константа;

<Идент>::= <Буква>

Идентификатор состоит из одной буквы;

<Const>::= <Цифра> <Const> | <Цифра>

Константа – последовательность цифр, состоящая хотя бы из одной цифры.

Лексический анализатор преобразует исходную программу в последовательность символов. Для удобства дальнейшей обработки лексем их разбивают на классы. В данном случае можно выделить следующие классы лексем:

1 – идентификатор;

2 – константа;

3 – символ присваивания;

4 – символы операций умножения и деления;

5 – символы операций сложения и вычитания.

Заметим, что необходимость разделения бинарных операций на две группы диктуется их различным приоритетом, играющим важную роль при генерации постфиксной записи.

Фрагмент программы лексического анализа:

/* prog - файл с транслируемой программой, lex - выходной файл лексем */

while(!feof (prog))

{

ch = readsym();

/* чтение очередного символа ch с пропуском пробелов */

if(isAlpha(ch))

fprintf(lex, "%c %d", ch, 1);

else

if(isDigit(ch))

digit();

/* Процедура чтения числа и вывода его в файл */

else

if(ch == '=')

fprintf(lex, "%c %d", ch, 3);

else

if(ch == '*' || ch == '/')

fprintf(lex, "%c %d", ch, 4);

else

if(ch == '+' || ch == '-')

fprintf(lex, "%c %d", ch, 5);

else

printf("Недопустимый символ языка - %c \n", ch);

}

0 1 0 0 1 0 1 1

управление последовательно передается в следующем порядке через состояния:

А, А, В, В, В, А, А, В, А.

Так как А есть последнее состояние, строка принимается конечным автоматом, однако при чтении строки

0 0 1 1 1

автомат проходит через состояния

А, А, А, В, А, В

поскольку В не является последним состоянием, эта строка не принимается, т.е. она не принадлежит языку, принимаемому этим автоматом. В связи с тем, что нули не влияют на состояние автомата, а каждая единица изменяет его состояние с А на В и с В на А, и начальное состояние является тем же, что и последнее состояние, язык, принимаемый автоматом, состоит из тех строк, которые содержат четное число единиц.

Переходы можно представить с помощью таблицы (таблица 6.1) и схематически (рис.6.1).

Состояния
Вход		А	В
	А	В
	В	А

Таблица 6.1

Такой автомат называют детерминированным, потому что в каждом элементе таблицы переходов содержится одно состояние. В недетерминированном конечном автомате это положение не выдерживается.

Рассмотрим конечный автомат, определяемый следующим образом:
M ₁ = (K ₁, S ₁, d ₁, S ₁, f ₁),

Где K ₁ = { A, В }, S ₁= {0,1}, S ₁ = { А }, f ₁= { В },

а переходы представлены в таблице 6.2 и на рис.6.2:

Таблица 6.2

Состояния
Вход		А	В
	Ø	{ В }
	{ A,В }	{ B }

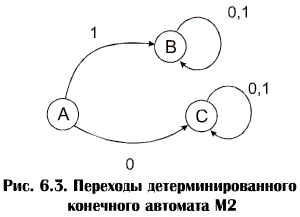
Первая строка будет принята, так как имеется переход (последовательность переходов), ведущий к последнему состоянию при чтении строки. Имеется также переход к непоследнему состоянию, но это не влияет на приемлемость строки. Поэтому прежде чем прийти к выводу о том, что строка не может быть принята недетерминированным конечным автоматом, необходимо перепробовать все возможные последовательности переходов.

Существует детерминированный конечный автомат М₂, соответствующий автомату М ₁, который принимает тот же язык. Переходы автомата М₂ приведены в таблице 6.3 и на рис.6.3.

M ₂ = (K ₂, S₂, d₂, S ₂, f ₂), где K ₂ = { A, В, C }, S₂= {0,1}, S ₂ = { А }, f ₂= { В }

Таблица 6.3

Состояния
Вход		А	В	C
	C	В	C
	В	B	C

Как и М ₁, М ₂ принимает строки из нулей и единиц тогда и только тогда, когда строка начинается с единицы. Однако при распознавании строки с помощью М ₂ возврат никогда не требуется, т.к. в процессе чтения определенного входного символа из любого состояния произойдет точно один переход к другому состоянию. Это значит, что при использовании М ₂время распознавания строки будет пропорционально ее длине.

Соответствие лексическому анализу заключается в том, что каждому языку типа 3 соответствует детерминированный конечный автомат, который распознает строки этого языка. Например, строки, генерируемые грамматикой G ₁c порождающими правилами:

А ® 1 А | 1 В | 1

В ® 0 В | 1 В | 0 | 1

где А – начальный символ, распознаются с помощью М ₁ или М ₂. Грамматику получают из недетерминированного конечного автомата М ₁ следующим образом:

1. Начальное состояние автомата становится начальным символом предложения грамматики.

2. Переходам

d (А, 1) = А,

d (А, 1) = В,

d (В, 0) = В,

d (В, 1) = В.

соответствуют порождающие правила

А ® 1 А | 1 В

В ® 0 В | 1 В

тому, что в состоянии А есть переход при чтении 1 к последнему состоянию В соответствует

А ® 1

и аналогично

В ® 0 | 1

Можно также, наоборот, из грамматики вывести автомат М ₁.

Автоматы Мили.

(Конечный) автомат Мили есть пятерка А=(Z, X, Y, f, g). Здесь Z, X, Y - конечные множества (множества состояний, входов и выходов соответственно), а f и g - отображения (функции переходов и выходов соответственно), причем
f: Z * X --> Z и g: Z * X --> Y, g -сюръекция.

Равенство f (z, x)=z' означает, конечно, что при входе х автомат, находящийся в состоянии z, переходит в состояние z', а равенство g (z, x)=y означает, что при этом на выходе появляктся y.

Требование сюръективности для отображения g не является существенным ограничением. Действительно, в Y не имеет смысла включать элементы, которые заведомо не могут появиться на выходе. Часто, однако, множество выходов определяют "с запасом", т.е. большим, чем это необходимо в действительности.

Автоматы Мура.

(Конечный) автомат Мура есть пятерка А=(Z, X, Y, f, h). Здесь Z, X, Y и f означают то же, что и в определении автомата Мили, а h - сюръективное отображение из Z в Y, называемое функцией выходов.

Замечание

Как и в случае автоматов Мили, предполагается, что множества Z, X и Y не пусты. Ясно, что автоматы Мура (как и автоматы Мили) могут быть описаны не только ориентированными графами, но и таблицей для функций f и h или матрицей переходов и таблицей для h.

Определение

Автомат Мили A = (Z, X, Y, f, g) называется автоматом Мили с конечной памятью, если для него существуют натуральные числа p, q и отображение h: X ^p+1 * Y ^q Y такие, что для всех z из Z и всех слов w = x₁... x_k из F(X), где k > max (p, q), выполнено равенство

y_k=h(x_k, x_k-1,..., x_k-p, y_k-1, y_k-2,..., y_k-q)

[ При этом считается, что y₁... y_k = g * (z, x₁... x_k) ].

Наименьшее число m, для которого существуют не превышающие его числа p и q, т.е. m=max(p, q),удовлетворяющие приведенному выше условию, называется памятью автомата Мили А.

Итак, автомат Мили имеет конечную память m, если существует функция h, с помощью которой выход в любой наперед заданный момент времени k может быть определен только по входу x_k в этот момент и по входам и выходам x_k-1,..., x_k-m и
y_k-1,..., y_k-m в предыдущие m моментов времени, без учета состояний автомата.

Минимальные автоматы Мура.

Очевидно, сокращенный автомат Мура имеет минимальное число состояний среди всех эквивалентных ему автоматов. Дадим соответствующее определение.

Определение

Автомат Мура А называется минимальным, если каждый эквивалентный ему автомат Мура имеет по меньшей мере столько же состояний, что и А.

Этапы синтеза автоматов.

В теории автоматов процесс синтеза автомата принято подразделять на отдельные этапы.

На первом, или предварительном, этапе синтеза формулируются (часто словесно) условия работы автомата, т. е. определяются условия его взаимодействия с другими устройствами или какими-либо объектами; выявляются необходимые входы и выходы автомата и намечается общий закон появления выходных сигналов в зависимости от воздействия на входы автомата. При синтезе достаточно сложного автомата часто его разбивают на отдельные блоки. В этом случае первый этап синтеза иногда называют этапом блочного синтеза автомата.

В Институте кибернетики АН УССР под руководством акад. В. М. Глушкова разработана формализованная методика блочного синтеза ЭВМ, позволяющая получать более экономичные решения, чем при интуитивном методе.

М. А. Гаврилов разработал блочный метод синтеза, позволяющий синтезировать один сложный автомат из простых блоков, выполняющих отдельные его функции. Такой метод дает возможность упростить формулировку условий работы (на языке таблиц переходов) и процесс построения автомата.

На этом этапе в настоящее время условия работы УА принято задавать в виде процессов управления на естественном или одном из формализованных языков, в частности на широко распространенном языке сетей Петри.

На втором этапе синтеза выявляются закон функционирования автомата (его функции переходов и функции выходов) и формальное описание автомата одним из принятых для этого способов. Этот этап синтеза принято называть этапом абстрактного синтеза или синтезом абстрактного автомата.

На этапе абстрактного синтеза автомата не интересуются теми физическими элементами, из которых он должен состоять. Нет нужды рассматривать, какие значения могут принимать входы, выходы и элементы памяти автомата. Важно знать лишь число возможных различных состояний входов и выходов автомата, число различных его внутренних состояний, а также законы изменения внутренних состояний автомата и выработки им тех или иных состояний выходов