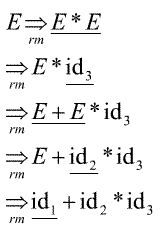Восходящий синтаксический анализ.

В этом разделе будет рассмотрен основной метод восходящего синтаксического анали­за, известный как синтаксический анализ типа " перенос/свертка " (shift-reduce) и называе­мый далее сокращенно ПС-анализом.

ПС-анализ пытается строить дерево разбора для входной строки, начиная с листьев (снизу) и работая по направлению к корню дерева (вверх). Этот процесс можно рассмат­ривать как свертку строки w к стартовому символу грамматики. На каждом шаге свертки (reduction step) некоторая подстрока, соответствующая правой части продукции, заменя­ется символом из левой части этой продукции, и если на каждом шаге подстроки выби­раются корректно, то мы получаем обращенное правое порождение.

Пример:

Рассмотрим грамматику

S ® aABe

A ® Abc | b

B ® d

Предложение abbcde сводится к S с помощью следующих шагов:

abbcde

aAbcde

aA.de

аАВе

S

Мы сканируем строку abbcde в поисках подстроки, соответствующей правой части какой-либо продукции. Такими подстроками являются b и d. Выберем крайнее слева b и заменим его нетерминалом А, который представляет собой левую часть продукции А ® b; таким образом, получим строку aAbcde. Теперь правым частям продукций соответствуют подстроки Abc, b и d. Хотя b и является крайней слева подстрокой, соответствующей правой части одной из продукций, выберем для замены подстроку Abc и заменим ее нетерминалом А в соответствии с продукцией А ® Abc. В результате получим строку aAde. Заменяя d на В, левую часть продукции В ® d, получаем аАВе, которая в соответствии с первой продукцией заменяется стартовым символом S. Итак, последовательность из четырех сверток позволяет привести строку abbcde к стартовому символу S. Эти сокращения представляют собой обращенное (т.е. записанное в обратном порядке) правое приведение

 

 

Основы.

Неформально говоря, основа, или дескриптор (handle) строки – это подстрока, которая совпадает с правой частью продукции и свертка которой в левую часть продукции представляет собой один шаг обращенного правого порождения. Во многих случаях крайняя слева подстрока β соответствующая правой части некоторой продукции А ® β не является основой, поскольку свертка в соответствии с продукцией А ® β приводит к строке, которая не может быть свернута к стартовому символу. Если в предыдущем примере мы заменим во второй строке aAbcde символ b нетерминалом А, то получим строку aAAcde, которая не может быть свернута в S. По этой причине нам следует дать более точное определение основы.

Говоря формально, основа правосентенциальной формы γ является продукцией А ® β и позицией строки β в γ,такими, что β может быть заменена нетерминалом А для получения предыдущей правосентенциальной формы в правом порождении γ. Таким образом, если,

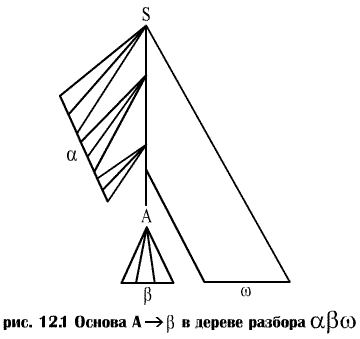
то А ® β в позиции после а представляет собой основу строки αβw. Строка w справа от основы содержит только терминальные символы. Заметим, что грамматика может быть неоднозначной, с несколькими правыми порождениями αβw. Если грамматика однозначна, то каждая правосентенциальная форма грамматики имеет ровно одну основу.

В приведенном выше примере abbcde представляет собой правосентенциальную форму, основой которой является А ® β в позиции 2. Аналогично aAbcde представляет собой правосентенциальную форму, дескриптор которой – А ® Abc в позиции 2. Иногда мы будем говорить "подстрока β представляет собой основу αβw ", если позиция β и продукция А ® β определяются однозначно.

На рис.12.1 изображена основа А ® β в дереве разбора правосентенциальной формы αβw. Основа представляет крайнее слева завершенное поддерево, состоящее из узла и всех его потомков. На рис.12.1 узел А — нижний крайний слева внутренний узел, все потомки которого находятся в дереве. Свертку β к А в αβw можно представить как "обрезку основы", т.е. удаление из дерева разбора всех потомков А.

Пример 12.a

Рассмотрим следующую грамматику

(1) Е ® E + E

(2) Е ® Е * Е

(3) E ® (E) (12.1)

(4) E ® id

и правое порождение

Для удобства мы пометили подстрочными индексами id и подчеркнули основу каждой правосентенциальной формы. Например, id₁ представляет собой основу право-сентенциальной формы id₁+id₂*id₃, поскольку id является правой частью продукции Е ®id, и замена id₁ на E приведет к предыдущей правосентенциальной форме E +id₂*id₃. Обратите внимание на то, что строка справа от основы состоит только из терминальных символов.

Поскольку грамматика (12.1) неоднозначна, имеется еще одно правое порождение той же строки:

Рассмотрим правосентенциальную форму E + E *id₃. В этом порождении E + E – основа E + E *id₃, в то время как в ранее представленном порождении ее основой яв­ляется id₃.

Первое порождение дает оператору * больший приоритет, чем оператору +, в то время как во втором порождении выше приоритет оператора +.

Обрезка основ.

Обращенное правое порождение может быть получено посредством " обрезки основ ". Мы начинаем процесс со строки терминалов w, которую хотим проанализировать. Если w – предложение рассматриваемой грамматики, то w = γ_n, где γ_n – п-я правосентенциальная форма некоторого, еще неизвестного правого порождения

Для воссоздания этого порождения в обратном порядке мы находим основу β_n в γ_n и заменяем ее левой частью продукции А_n ® β_n, для получения (n -1)-й сентенциальной формы γ_{n- 1}. Заметим, что пока мы не знаем, каким образом искать основы, но вскоре познакомимся с соответствующими методами.

Затем мы повторяем описанный процесс, т.е. находим в γ_{n- 1} основу β_n-1 и свертываем ее для получения правосентенциальной формы γ_{n- 2}. Если после очередного шага правосентенциальная форма содержит только стартовый символ S, мы прекращаем процесс и сообщаем об успешном завершении анализа. Обращенная последовательность продукций, использованных в свертках, представляет собой правое порождение входной строки.

Пример 12.b

Рассмотрим грамматику (12.1) из примера 12.a и входную строку id₁+id₂*id₃. Последовательность сверток, приводящая входную строку к стартовому символу E, показана в таблице 12.1. Следует отметить, что последовательность правосентенциальных форм в этом примере представляет собой обращение первой последовательности правых порождений из примера 12.a.

 

 

Таблица 12.1. Свертки, выполняемые ПС-анализатором

правосентенциальная форма	основа	сворачивающая продукция
id1+id2*id3	id1	Е ®id
E +id2*id3	id2	Е® id
E + E *id3	id3	Е® id
E+E*E	E*E	Е® E*E
E + E	E+E	Е® E+E
Е