Двухуровневые и атрибутивные грамматики.

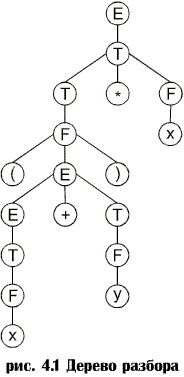
Двухуровневые грамматики (W-грамматики, названной так в честь их изобретателя – А. ван Вейнгаардена). Идея применения двухуровневой грамматики состоит в том, что если правила обычной грамматики обеспечивают конечный способ описания языка, состоящего из бесконечного числа строк, то здесь вторая грамматика применяется для генерирования бесконечного числа правил, которые в свою очередь генерируют предложения языка. Применение второй грамматики позволяет избежать рутинной работы, связанной с написанием бесконечного числа порождающих правил. С помощью двухуровневой грамматики можно генерировать любой язык типа 0. Данная концепция является даже слишком мощной (КЗ свойства большинства машинных языков относительно просты).

Атрибутивные грамматики. Атрибуты применяются для описания КЗ (точнее К-несвободных) аспектов языка. Рассмотрим пример. Пусть в некотором языке идентификаторы могут иметь тип int или char и являются терминалами грамматики. Описание с помощью КС порождающих правил.

D ® int I

D ® char I

Описав идентификатор, мы хотим запомнить его тип. Этот тип будет свойством описания, видоизменим грамматику, чтобы это указать:

D (.ID, MODE)®int(.MODE1)I (.ID1)

ID = ID1

MODE = MODE1

аналогично для char. MODE, MODE1, ID, ID1 пишутся в скобках после терминала или нетерминала грамматики и представляют собой его признаки (атрибуты). Преимущество атрибутивных грамматик в том, что они выглядят как КС, но могут специфицировать КЗ конструкции языка. Фактически любой язык типа 0 можно описать с помощью атрибутивной грамматики. Так как языки программирования представляется как КС, к которым добавляются контекстные ограничения, атрибутивные грамматики хорошо подходят для их описания.

Проблема разбора.

Компилятор должен решить проблему проверки строк символов, чтобы определить, принадлежат ли они данному языку, и если да, то распознать структуру строк в терминах порождающих правил грамматики. Эта проблема известна какпроблема разбора. Исследуем грамматику с порождающими правилами (E - начальный символ).

1. Е ® Е + Т

2. Е ® T

3. T ® T * F

4. T ® F

5. F ® (Е)

6. F ® x

7. F ® y

Ясно, что строка (x + y) * x принадлежит данному языку. В частности, это можно вывести следующим образом (для каждого шага вывода указан номер применяемого правила):

2) E Þ T

3) Þ T * F

4)) Þ F * F

5) Þ (E)* F

1) Þ (E + T) * F

2) Þ (T + T) * F

4) Þ (F + T) * F

6) Þ (x + T)*F

4) Þ (x + F) * F

7) Þ (x + y) * F

6) Þ (x + y) * x

Или же это можно вывести так:

2) E Þ T

3) Þ T * F

6) Þ T * x

4) Þ F * x

5) Þ (E) * x

1) Þ (E + T) * x

4) Þ (E + F) * x

7) Þ (E + y) * x

2) Þ (T + y) * x

4) Þ (F + y) * x

6) Þ (x + y) * x

На каждом этапе первого вывода самый левый нетерминал в сентенциальной форме замещался с помощью одного из порождающих правил грамматики. Поэтому данный вывод называется левосторонним. Второй вывод, на каждом этапе которого замещается самый правый нетерминал, называется правосторонним. Существуют также другие выводы, не являющиеся ни лево-, ни правосторонними, однако при реализации трансляторов они практически не используются.

Проблему разбора можно свести к

1) нахождению левостороннего разбора;

2) нахождению правостороннего разбора;

3) построению синтаксического дерева.

Левосторонний и правосторонний разбор.

Левосторонний разбор предложения определяется как последовательность порождающих правил, применяемая для генерирования предложения посредством левостороннего вывода. В данном случае левосторонний разбор можно записать как

2,3,4,5,1,2,4,6,4,7,6.

Правосторонний разбор предложения является обратной последовательностью порождающих правил, используемых для генерирования предложения посредством правостороннего вывода; например, в вышеприведенном случае правосторонний разбор запишется в виде

6,4,2,7,4,1,5,4,6,3,2.

Обратный порядок последовательности порождающих правил связан с тем, что правосторонний разбор обычно ассоциируется с приведением предложения к начальному символу, а не с генерированием предложения из начального символа (см. ниже разбор снизу вверх). Заметим, что каждое порождающее правило используется в обоих выводах (или разборах) одинаковое число раз.

Дерево разбора.

Дерево разбора. Вывод может быть описан также в терминах построения дерева, известного как синтаксическое дерево (или дерево разбора). В случае со строкой

(x + y) * x

синтаксическое дерево будет таким, как показано на рис. 4.1.

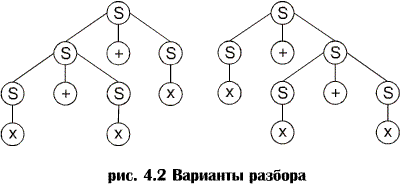
Неоднозначные грамматики.

Неоднозначные грамматики. В большинстве случаев левосторонний и правосторонний разборы и синтаксическое дерево являются уникальными. Однако для грамматики с порождающими правилами:

S ® S+S | x

предложение x + x + x имеет два синтаксических дерева (рис. 4.2) и два левосторонних (и правосторонних) разбора:

 

 

S Þ S + S	S Þ S + S
Þ S + S + S	Þ x + S
Þ x + S + S	Þ x + S + S
Þ x + x + S	Þ x + x + S
Þ x + x + x	Þ x + x + x

Если какое-либо предложение, генерированное грамматикой, имеет более одного дерева разбора, о такой грамматике говорят, что она неоднозначна. Эквивалентное условие заключается в том, что предложение должно иметь более одного левостороннего или правостороннего разбора. Задача установления неоднозначности грамматики является, в общем случае, неразрешимой, т.е. не существует универсального алгоритма, который принимал бы на входе любую грамматику и определял бы, однозначна она или нет. Некоторые неоднозначные грамматики можно преобразовать в однозначные, генерирующие тот же язык. Например, грамматика с порождающими правилами

S ® x | S + x

является однозначной и генерирует тот же язык, что и рассмотренная ранее неоднозначная грамматика.

Методы разбора обычно бывают нисходящими, т.е. начинают с начального символа и идут к предложению, или восходящими, т.е. начинают с предложения и идут к начальному символу.

Отказ от решения в разборе называют возвратом. Методы разбора могут быть недетерминированными и детерминированными в зависимости от того, возможен возврат или нет. Недетерминированные методы разбора весьма дорогие с точки зрения памяти и времени и крайне затрудняют включение в синтаксический разбор анализатор действий, выполняемых во время компиляции, результаты которых позднее должны быть аннулированы (например, построение таблицы символов и т.п.). В дальнейшем мы будем рассматривать лишь детерминированные методы разбора. Основное внимание в настоящем учебном пособии уделено методам нисходящего разбора, они же используются в лабораторных работах и при курсовом проектировании. Методы восходящего разбора рассмотрены в отдельной главе.