Автоматы Мили с конечной памятью.

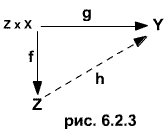
Каждое состояние автомата Мили однозначно (т.е. с точностью до эквивалентности) определяется конечным набором входных слов вместе с соответствующими выходными словами. Это означает, что автомат Мили может "содержать" только конечное множество входно-выходных связей. Поэтому выход зависит только от некоторого ограниченного числа предыдущих входов. Мы увидим, однако, что здесь не существует функциональной зависимости, даже при использовании выходов в предыдущие моменты времени в качестве дополнительных аргументов.

Определение

Автомат Мили A = (Z, X, Y, f, g) называется автоматом Мили с конечной памятью, если для него существуют натуральные числа p, q и отображение h: X ^p+1 * Y ^q Y такие, что для всех z из Z и всех слов w = x₁... x_k из F(X), где k > max (p, q), выполнено равенство

y_k=h(x_k, x_k-1,..., x_k-p, y_k-1, y_k-2,..., y_k-q)

[ При этом считается, что y₁... y_k = g * (z, x₁... x_k) ].

Наименьшее число m, для которого существуют не превышающие его числа p и q, т.е. m=max(p, q),удовлетворяющие приведенному выше условию, называется памятью автомата Мили А.

Итак, автомат Мили имеет конечную память m, если существует функция h, с помощью которой выход в любой наперед заданный момент времени k может быть определен только по входу x_k в этот момент и по входам и выходам x_k-1,..., x_k-m и
y_k-1,..., y_k-m в предыдущие m моментов времени, без учета состояний автомата.

Входно-независимые автоматы Мили.

При формальном сравнении определений автомата Мили и автомата Мура может показаться, что автоматы Мура могут быть заданы как автоматы Мили, у которых выход не зависит от входа, т.е. как автоматы Мили, выходная функция которых удовлетворяет условию: для всех х и х' из Х и всех z из Z выполняется g(z, x) = g(z, x'). Автоматы Мили с этим свойством называются входно-независимыми.

Минимальные автоматы Мура.

Очевидно, сокращенный автомат Мура имеет минимальное число состояний среди всех эквивалентных ему автоматов. Дадим соответствующее определение.

Определение

Автомат Мура А называется минимальным, если каждый эквивалентный ему автомат Мура имеет по меньшей мере столько же состояний, что и А.

Автоматы Мили представимые как автоматы Мура.

Нашему представлению о способе функционирования автоматов Мура в большей степени отвечает следующее представление о них как о частных случаях автоматов Мили: пусть А - автомат Мура. Положим g (z, x) = h (f (z, x)) длякаждого z из Z и каждого x из X. Тогда В = (Z, X, Y, f, g) - автомат Мили, который для всех непустых входных последовательностей порождает такие же выходные последовательности, как и автомат А, если, конечно, не учитывать самый первый выход автоматат А. Следует отметить, что при переходе от автоматов одного вида к автоматам другого вида необходимо изменение содержательных представлений, используемых при определении состояний автоматов.

И наоборот, можно сказать, что автомат Мили В = (Z, X, Y, f, g) представим как автомат Мура, если существует отображение h такое, что диаграмма на рис. 6.2.3 является коммутативной.

Действительно, в этом случае из равенства f (z, x) = f (z', x') при произвольных z и z' из Z и произвольных x и x' из X вытекает равенство g (z, x) = g (z', x'). Поэтому на всех ребрах, входящих на графе автомата B в одну вершину (состояние), должен быть указан один и тот же выход. Присоединяя этот выход к данному состоянию (рис. 6.2.3а), получаем автомат Мура
A (Z, X, Y, f, h), который (если не учитывать его первый выход) имеет такое же входно-выходное поведение, как и автомат B.

Этапы синтеза автоматов.

В теории автоматов процесс синтеза автомата принято подразделять на отдельные этапы.

На первом, или предварительном, этапе синтеза формулируются (часто словесно) условия работы автомата, т. е. определяются условия его взаимодействия с другими устройствами или какими-либо объектами; выявляются необходимые входы и выходы автомата и намечается общий закон появления выходных сигналов в зависимости от воздействия на входы автомата. При синтезе достаточно сложного автомата часто его разбивают на отдельные блоки. В этом случае первый этап синтеза иногда называют этапом блочного синтеза автомата.

В Институте кибернетики АН УССР под руководством акад. В. М. Глушкова разработана формализованная методика блочного синтеза ЭВМ, позволяющая получать более экономичные решения, чем при интуитивном методе.

М. А. Гаврилов разработал блочный метод синтеза, позволяющий синтезировать один сложный автомат из простых блоков, выполняющих отдельные его функции. Такой метод дает возможность упростить формулировку условий работы (на языке таблиц переходов) и процесс построения автомата.

На этом этапе в настоящее время условия работы УА принято задавать в виде процессов управления на естественном или одном из формализованных языков, в частности на широко распространенном языке сетей Петри.

На втором этапе синтеза выявляются закон функционирования автомата (его функции переходов и функции выходов) и формальное описание автомата одним из принятых для этого способов. Этот этап синтеза принято называть этапом абстрактного синтеза или синтезом абстрактного автомата.

На этапе абстрактного синтеза автомата не интересуются теми физическими элементами, из которых он должен состоять. Нет нужды рассматривать, какие значения могут принимать входы, выходы и элементы памяти автомата. Важно знать лишь число возможных различных состояний входов и выходов автомата, число различных его внутренних состояний, а также законы изменения внутренних состояний автомата и выработки им тех или иных состояний выходов при поступлении на его входы той или иной последовательности состояний входа.

Исследование абстрактного синтеза автоматов было начато С. К. Клини, которым был предложен так называемый язык регулярных событий. В дальнейшем абстрактный синтез автомата, основанный на использовании этого языка, был усовершенствован В. М. Глушковым, который разработал алгоритм абстрактного синтеза, годный для программирования на ЭВМ.

Другим языком, на котором базируется абстрактный синтез автомата, является язык исчисления предикатов, исследованный Б. А. Трахтенбротом.

Результатом второго этапа синтеза является задание автомата одним из стандартных способов, к которым относятся таблицы и матрицы переходов, а также таблицы включений и диаграммы переходов.

В некоторых случаях удобно задавать автомат временными функциями, а МА — логическими схемами алгоритмов.

На втором этапе синтеза, очевидно, выявляется и емкость памяти автомата. При этом, несмотря на стремление получить уже при абстрактном синтезе автомат с минимальным числом внутренних состояний, в ряде случаев получаем автоматы, у которых число внутренних состояний заметно отличается от минимального. В связи с этим на следующем,третьем этапе производится минимизация числа внутренних состояний автомата.

На четвертом этапе синтеза производится кодирование или, как говорят, размещение внутренних состояний. Этот этап находится на грани абстрактного и структурного рассмотрения автомата. После кодирования внутренних состояний автомата, состояний входа и выхода выписываются канонические уравнения.

На пятом этапе синтеза завершается выбор структуры автомата построением так называемой функциональной схемы комбинационной части автомата (однотактной схемы) или, как говорят, логического преобразователя. При этом синтез автомата с памятью (многотактной схемы) сводится к синтезу автомата без памяти (однотактной схемы) с помощью понятия однотактного эквивалента.

В настоящее время этот этап синтеза в теории автоматов наиболее развит.

Шестой этап синтеза включает электрический или другой расчет элементов схемы и моделирование автомата с целью проверки его работоспособности.

На седьмом этапе осуществляется размещение деталей на платах, составление монтажных схем и технической документации. При использовании интегральных схем и особенно схем с большой и сверхбольшой степенью интеграции (БИС и СБИС) на этом этапе осуществляется размещение элементов функциональной схемы по корпусам, а затем размещение корпуса на стандартных платах, часто называемых типовыми элементами замены (ТЭЗ) —типовые элементы замены по блокам и блоки по шкафам.

Разделение процесса синтеза на этапы, с одной стороны, облегчает процесс построения автомата, а с другой стороны, может привести к усложнению его структуры. Так, рассматривая на отдельных этапах процессы минимизации числа внутренних состояний, кодирование внутренних состояний и синтез структуры логического преобразователя, можно прийти к менее оптимальному решению по сравнению с тем случаем, когда, эти три этапа были бы совмещены. Этот недостаток пытаются уменьшить тем, что на каждом этапе синтеза стараются учесть его влияние на следующий этап.

Разделение процесса синтеза автомата на такие семь этапов является достаточно условным, хотя это и позволяет облегчить решение всей задачи синтеза автомата. Часто некоторые этапы синтеза не разделяются между собой, а иногда просто опускаются.

Следует заметить, что наряду с изложенным выше делением процесса синтеза в последнее время весь процесс проектирования сложного управляющего автомата чаще подразделяют на более крупные этапы: системное, программно-логическое, техническое и технологическое проектирование.