Лексемы. Фаза лексического анализа.

Первой фазой процесса компиляции является лексический анализ, то есть группирование строк литер, обозначающих идентификаторы, константы или слова языка и т.д., в единые символы (лексемы). Этот процесс может идти параллельно с другими фазами компиляции (например, в однопроходных компиляторах). Однако, в любом случае, при описании конструкции компилятора и его построения удобно представлять лексический анализ как самостоятельную фазу.

Блок сканирования (сканер) должен выдавать каждую лексему, устанавливая ее принадлежность тому или иному классу. Выбор классов зависит от особенностей транслируемого языка. Часто выделяют классы имен переменных, констант, ключевых слов, арифметических и логических операций ("+", "-", "*", "/" и т.д.), специальных символов ("=", ";" и т. д.)

Характер распознаваемых строк может намного упростить процесс лексического анализа. Например:

идентификаторы:

a1 one

числа:

100 10.54

ключевые слова языка:

begin if end

Все эти строки можно генерировать с помощью регулярных выражений. Например, вещественные числа можно генерировать посредством регулярного выражения (+ | -) d d *. d *, где d обозначает любую цифру. Из выражения видно, что вещественное число состоит из следующих компонентов, расположенных именно в таком порядке:

1. возможного знака;

2. последовательности из одной или более цифр;

3. десятичной точки;

4. последовательности из нуля или более цифр.

Регулярные выражения эквивалентны грамматикам типа 3. Например, грамматика типа 3, соответствующая регулярному выражению для вещественного числа, имеет порождающие правила:

R ® +S | -S | dQ

S ® d Q

Q ® d Q |.F |.

F ® d | dF

где R - начальный символ, d – цифра.

Существует полное соответствие между регулярными выражениями (а потому и грамматиками типа 3) и конечными автоматами, более подробно рассмотренными в следующей главе.

Некоторые лексемы (например, *) могут быть распознаны по одному считанному символу, другие (такие, как:=) – по двум символам, а для идентификации третьих необходимо прочитать неизвестное заранее число символов (например, код константы). В последнем случае, чтобы найти конец лексемы, приходится считывать один лишний символ, не входящий в состав данной лексемы. Этот символ необходимо запоминать, чтобы при разборе следующей лексемы он не был утерян.

Лексический анализатор, наряду с разбиением исходного потока символов на лексемы, может включать в исходный текст дополнительную информацию или исключать из него строки символов. Примером дополнительно включаемой информации являются номера строк. Если их не включить, то информация о том, в какой строке исходного текста находилась та или иная лексема, будет, в случае выполняющего сканирование в отдельном проходе компилятора, утеряна после лексического анализа. Однако для диагностики на фазе синтаксического анализа необходимо иметь возможность ссылаться на ошибки в программе с указанием номеров строк оригинального исходного текста. С другой стороны, комментарии включаются в текст программы или описания объекта проектирования только для предоставления читателю – человеку дополнительных пояснений. Они никак не влияют на генерируемый в дальнейшем код, и лексический анализатор обычно их просто исключает.

Пример структуры программы сканирования.

Пусть реализуемый язык состоит только из оператора присваивания БНФ языка:

<Присваивание>::= <Идент> = <Выражение>

Правило показывает, что в левой части присваивания – идентификатор, далее следует символ присваивания (=), справа – выражение;

<Выражение>::= <Операнд> | <Операнд> <Бин.оп> <Выражение>

Выражение – это операнд, или операнд, за которым следует бинарная операция и выражение;

<Бин.оп>::= "-" | "+" | "*" | "/"

Бинарная операция – символ арифметической операции " - ", " + "," * " или "/";

<Операнд>::= <Идент> | <Const>

Операнд – это идентификатор или константа;

<Идент>::= <Буква>

Идентификатор состоит из одной буквы;

<Const>::= <Цифра> <Const> | <Цифра>

Константа – последовательность цифр, состоящая хотя бы из одной цифры.

Лексический анализатор преобразует исходную программу в последовательность символов. Для удобства дальнейшей обработки лексем их разбивают на классы. В данном случае можно выделить следующие классы лексем:

1 – идентификатор;

2 – константа;

3 – символ присваивания;

4 – символы операций умножения и деления;

5 – символы операций сложения и вычитания.

Заметим, что необходимость разделения бинарных операций на две группы диктуется их различным приоритетом, играющим важную роль при генерации постфиксной записи.

Фрагмент программы лексического анализа:

/* prog - файл с транслируемой программой, lex - выходной файл лексем */

while(!feof (prog))

{

ch = readsym();

/* чтение очередного символа ch с пропуском пробелов */

if(isAlpha(ch))

fprintf(lex, "%c %d", ch, 1);

else

if(isDigit(ch))

digit();

/* Процедура чтения числа и вывода его в файл */

else

if(ch == '=')

fprintf(lex, "%c %d", ch, 3);

else

if(ch == '*' || ch == '/')

fprintf(lex, "%c %d", ch, 4);

else

if(ch == '+' || ch == '-')

fprintf(lex, "%c %d", ch, 5);

else

printf("Недопустимый символ языка - %c \n", ch);

}

Определение конечного автомата.

Существует полное соответствие между регулярными выражениями (а поэтому и грамматиками типа 3) и конечными автоматами, которые определяются следующим образом:

Конечный автомат – это устройство для распознавания строк какого-либо языка. У него есть конечное множество состояний, отдельные из которых называются последними. По мере считывания каждой литеры строки контроль передается от состояния к состоянию в соответствии с заданным множеством переходов. Если после считывания последней литеры строки автомат будет находиться в одном из последних состояний, о строке говорят, что она принадлежит языку, принимаемому автоматом. В ином случае строка не принадлежит языку, принимаемому автоматом.

Конечный автомат формально определяется пятью характеристиками:

-конечным множеством состояний (K)

-конечным входным алфавитом (S)

-множеством переходов (d)

-начальным состоянием (S ₀ Î K)

-множеством последних состояний (f Î K)

M = (K, S, d, S ₀, f).

Пример: Состояниями автомата являются А и В, входным алфавитом – {0,1}, начальным состоянием – А, множеством последних состояний – { A }, а переходами

d (А, 0) = А,

d (А, 1) = В,

d (В, 0) = В,

d (В, 1) = А.

Эти переходы означают, что при чтении 0 в состоянии А управление передается в состояние А и т.д. При чтении строки

0 1 0 0 1 0 1 1

управление последовательно передается в следующем порядке через состояния:

А, А, В, В, В, А, А, В, А.

Так как А есть последнее состояние, строка принимается конечным автоматом, однако при чтении строки

0 0 1 1 1

автомат проходит через состояния

А, А, А, В, А, В

поскольку В не является последним состоянием, эта строка не принимается, т.е. она не принадлежит языку, принимаемому этим автоматом. В связи с тем, что нули не влияют на состояние автомата, а каждая единица изменяет его состояние с А на В и с В на А, и начальное состояние является тем же, что и последнее состояние, язык, принимаемый автоматом, состоит из тех строк, которые содержат четное число единиц.

Переходы можно представить с помощью таблицы (таблица 6.1) и схематически (рис.6.1).

Состояния
Вход		А	В
	А	В
	В	А

Таблица 6.1

Такой автомат называют детерминированным, потому что в каждом элементе таблицы переходов содержится одно состояние. В недетерминированном конечном автомате это положение не выдерживается.

Рассмотрим конечный автомат, определяемый следующим образом:
M ₁ = (K ₁, S ₁, d ₁, S ₁, f ₁),

Где K ₁ = { A, В }, S ₁= {0,1}, S ₁ = { А }, f ₁= { В },

а переходы представлены в таблице 6.2 и на рис.6.2:

Таблица 6.2

Состояния
Вход		А	В
	Ø	{ В }
	{ A,В }	{ B }

Первая строка будет принята, так как имеется переход (последовательность переходов), ведущий к последнему состоянию при чтении строки. Имеется также переход к непоследнему состоянию, но это не влияет на приемлемость строки. Поэтому прежде чем прийти к выводу о том, что строка не может быть принята недетерминированным конечным автоматом, необходимо перепробовать все возможные последовательности переходов.

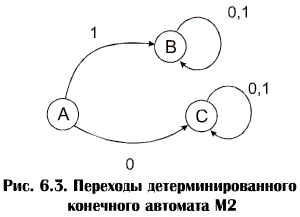
Существует детерминированный конечный автомат М₂, соответствующий автомату М ₁, который принимает тот же язык. Переходы автомата М₂ приведены в таблице 6.3 и на рис.6.3.

M ₂ = (K ₂, S₂, d₂, S ₂, f ₂), где K ₂ = { A, В, C }, S₂= {0,1}, S ₂ = { А }, f ₂= { В }

Таблица 6.3

Состояния
Вход		А	В	C
	C	В	C
	В	B	C

Как и М ₁, М ₂ принимает строки из нулей и единиц тогда и только тогда, когда строка начинается с единицы. Однако при распознавании строки с помощью М ₂ возврат никогда не требуется, т.к. в процессе чтения определенного входного символа из любого состояния произойдет точно один переход к другому состоянию. Это значит, что при использовании М ₂время распознавания строки будет пропорционально ее длине.

Соответствие лексическому анализу заключается в том, что каждому языку типа 3 соответствует детерминированный конечный автомат, который распознает строки этого языка. Например, строки, генерируемые грамматикой G ₁c порождающими правилами:

А ® 1 А | 1 В | 1

В ® 0 В | 1 В | 0 | 1

где А – начальный символ, распознаются с помощью М ₁ или М ₂. Грамматику получают из недетерминированного конечного автомата М ₁ следующим образом:

1. Начальное состояние автомата становится начальным символом предложения грамматики.

2. Переходам

d (А, 1) = А,

d (А, 1) = В,

d (В, 0) = В,

d (В, 1) = В.

соответствуют порождающие правила

А ® 1 А | 1 В

В ® 0 В | 1 В

тому, что в состоянии А есть переход при чтении 1 к последнему состоянию В соответствует

А ® 1

и аналогично

В ® 0 | 1

Можно также, наоборот, из грамматики вывести автомат М ₁.

Автоматы Мили.

(Конечный) автомат Мили есть пятерка А=(Z, X, Y, f, g). Здесь Z, X, Y - конечные множества (множества состояний, входов и выходов соответственно), а f и g - отображения (функции переходов и выходов соответственно), причем
f: Z * X --> Z и g: Z * X --> Y, g -сюръекция.

Равенство f (z, x)=z' означает, конечно, что при входе х автомат, находящийся в состоянии z, переходит в состояние z', а равенство g (z, x)=y означает, что при этом на выходе появляктся y.

Требование сюръективности для отображения g не является существенным ограничением. Действительно, в Y не имеет смысла включать элементы, которые заведомо не могут появиться на выходе. Часто, однако, множество выходов определяют "с запасом", т.е. большим, чем это необходимо в действительности.

Автоматы Мура.

(Конечный) автомат Мура есть пятерка А=(Z, X, Y, f, h). Здесь Z, X, Y и f означают то же, что и в определении автомата Мили, а h - сюръективное отображение из Z в Y, называемое функцией выходов.

Замечание

Как и в случае автоматов Мили, предполагается, что множества Z, X и Y не пусты. Ясно, что автоматы Мура (как и автоматы Мили) могут быть описаны не только ориентированными графами, но и таблицей для функций f и h или матрицей переходов и таблицей для h.