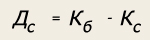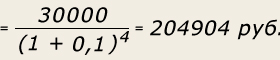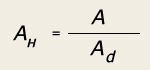Для этих целей используют два основных понятия —будущая стоимость денег и их настоящая стоимость.

Будущая стоимость денег представляет собой сумму инвестированных в настоящий момент средств, в которую они превращаются через определенный период времени с учетом определенной ставки процента.

Определение будущей стоимости денег связано с процессом наращения (компаудинга) стоимости денежных активов, который представляет собой поэтапное их увеличение путем присоединения к первоначальному их размеру суммы процента (процентных платежей). Эта сумма рассчитывается по так называемой «процентной ставке». В инвестиционных расчетах процентная ставка применяется не только как инструмент наращения стоимости денежных средств, но и в более широком понимании — как измеритель степени прибыльности инвестиционных операций предприятия.

Настоящая стоимость денег представляет собой сумму будущих денежных средств, приведенных с учетом определенной ставки процента (так называемой «дисконтной ставки») к настоящему периоду. Определение настоящей стоимости денег связано с процессом дисконтирования их стоимости во времени, который представляет операцию, обратную наращиванию при обусловленном будущем размере денежных средств. В этом случае сумма процента (дисконта) вычитается из конечной суммы (будущей стоимости) денежных средств. Такая ситуация возникает в тех случаях, когда необходимо определить, сколько денежных средств следует инвестировать сегодня для того, чтобы через определенный период времени получить заранее обусловленную их сумму.

При проведении финансовых расчетов, связанных с инвестированием средств и формированием инвестиционной прибыли, процессы наращения (компаундинга) и дисконтирования стоимости денежных средств целесообразно осуществлять как по простым, так и по сложным процентам.

Простые проценты применяются, как правило, при краткосрочном инвестировании, а сложные — при долгосрочном.

Простым процентом называется сумма, которая начисляется по первоначальной (настоящей) стоимости вклада в конце отчетного периода платежа (месяца, квартала и т.д.), обусловленного условиями инвестирования средств.

При расчете суммы простого процента в процессе наращения (компаундинга) вклада можно использовать формулу:

где И n — сумма процента за обусловленный период инвестирования в целом;
К — первоначальная сумма вклада;
n — продолжительность инвестирования (выраженная количеством периодов, по которым осуществляется каждый процентный платеж);
C n — используемая процентная ставка, выраженная десятичной дробью.

В этом случае будущая стоимость вклада (К б) с учетом начисленной суммы процента определяется по формуле:

Пример. Необходимо определить сумму процента за год при следующих условиях:
первоначальная сумма вклада — 300 тыс. руб;процентная ставка — 10% в квартал.

Подставляя эти значения в формулу, получим сумму процента

И n = 300 000 • 4 • 0,1 = 120 000 руб.

Будущая стоимость вклада составит:

К б = 300 000 + 120 000 руб. = 420 000 руб.

Значение (1 +ncn) называется коэффициентом, или множителем, наращения суммы простых процентов. Его значение всегда больше единицы.

При расчете суммы простого процента в процессе дисконтирования стоимости денежных средств (т.е. суммы дисконта) можно использовать формулу:

Пример. Необходимо определить сумму дисконта по простому проценту за год при следующих условиях:

конечная сумма вклада — 300 тыс. руб.;

дисконтная ставка — 10% в квартал.

Подставляя эти значения в формулу расчета суммы дисконта, получим:

Д = 300 000 – 300 000(1/1+4 x 0,1)= 85 714 руб.

Соответственно настоящая стоимость инвестиционных затрат, необходимых для получения через год 300 тыс. руб., должна составить:
К = 300 000 — 85 714 = 214 286 руб.

Сложным процентом называется сумма прибыли, которая образуется в результате инвестирования при условии, что сумма начисленного простого процента не выплачивается после каждого периода, а присоединяется к сумме основного вклада и в последующем платежном периоде сама приносит доход.

При расчете суммы вклада в процессе его наращения по сложным процентам можно использовать формулу:

где К бс — будущая стоимость вклада при его наращении по сложным процентам.

Соответственно сумма процента (И n) определяется по формуле:

 

Пример. Необходимо определить будущую стоимость вклада и сумму сложного процента за весь период инвестирования при следующих условиях:

-первоначальная стоимость вклада — 300 тыс. руб.;

-процентная ставка, используемая при расчете суммы сложного процента, ус-тановлена в размере 10% в квартал;

-общий период инвестирования — один год.

Подставляя эти показатели в вышеприведенные формулы, получим:
будущая стоимость вклада

сумма процента составит 139 230 руб. (439 230 – 300 000).

При расчете настоящей стоимости денежных средств в процессе дисконтирования посложным процентамможно использовать формулу:

где K с — первоначальная сумма вклада при расчетах по сложным процентам.

Сумма дисконта (Дс) определяется по формуле:

Пример. Необходимо определить настоящую стоимость денежных средств и сумму дисконта по сложным процентам за год при следующих условиях:
будущая стоимость денежных средств — 300 тыс. руб.;
используемая для дисконтирования ставка сложного процента — 10% в квартал.
Подставляя эти значения в формулу, получим:

Настоящая стоимость

Сумма дисконта составит 95 096 руб. (300 000 – 204 904).

При оценке стоимости денег во времени необходимо иметь в виду, что на результат оценки оказывают большое влияние не только используемая ставка процента, но и периодичность выплат (или количество платежных периодов) в течение одного и того же общего срока. Иногда оказывается более выгодным инвестировать деньги под меньшую ставку процента, но с большей периодичностью выплат.

Пример. Перед инвестором стоит задача разместить 300 тыс. руб. на депозитный вклад сроком на один год. Один банк предлагает инвестору выплачивать доход по сложным процентам в размере 7,5% в квартал, второй — в размере 10% один раз в четыре месяца, третий — в размере 15% два раза в год, четвертый — в размере 30% один раз в году.

Для того чтобы определить, какой вариант инвестирования лучше, составим табл. 7.7.
Сравнение вариантов показывает, что наиболее эффективным является 1-й вариант (выплата дохода в размере 7,5% один раз в квартал).

Таблица 7.7
Расчет будущей стоимости вклада при различных условиях
инвестирования, руб.

Вариант	Настоящая стоимость вклада	Ставка процента	Будущая стоимость в конце
1-го периода	2-го периода	3-го периода	4-го периода
		7,5		346687,5
		10,0				-
		15,0			-	-
		30,0		-	-	-

Отдельные виды денежных потоков, оцениваемых во времени, осуществляются последовательно через равные промежутки времени и по одинаковой ставке процента. Такая равномерность денежных потоков (равномерных платежей) носит название аннуитет.

Примером аннуитета могут быть ежеквартальные суммы процентов по купонным облигациям или сберегательным сертификатам, равномерная уплата взносов за арендуемое имущество и т.п.

Представление последовательности денежных потоков (платежей) в виде аннуитета существенно облегчает процесс наращения или дисконтирования стоимости денег, дает возможность использовать набор упрощенных формул со стандартными значениями отдельных показателей, проводимых в специальных таблицах. Так, для определения будущей стоимости аннуитета можно использовать формулу:

где А б — общая будущая стоимость аннуитета на конец определенного периода;
А — сумма аннуитетного платежа;
dа — коэффициент наращения стоимости аннуитета, определяемый по специ-альным таблицам с учетом принятой ставки процента и числа периодов.

Соответственно формула для определения настоящей стоимости аннуитета будет иметь вид:

где А н — настоящая стоимость аннуитета;
А — сумма аннуитетного платежа;
А d — дисконтный коэффициент аннуитета, определяемый по специальным таблицам с учетом принятой дисконтной ставки и числа периодов.

С концепцией оценки стоимости денег во времени, как уже отмечалось, связан и фактор инфляции, которая с течением времени обесценивает стоимость денежных средств. Это связано с тем, что рост инфляции (индекса средних цен) вызывает соответствующее снижение покупательной способности денег.

При расчетах, связанных с корректировкой денежных потоков в процессе инвестирования с учетом инфляции, принято использовать два основных понятия — номинальная и реальная сумма денежных средств.

Номинальная сумма денежных средств представляет собой оценку ее величины без учета изменения покупательной способности денег.

Реальная сумма денежных средств представляет собой оценку ее величины с учетом изменения покупательной способности денег в связи с процессом инфляции. Такая оценка может проводиться при определении как настоящей, так и будущей стоимости денежных средств.

В процессе оценки инфляции используют два основных показателя:
1) темп инфляции (Т i), характеризующий прирост среднего уровня цен в рассматриваемом периоде (n), выражаемый в инвестиционных расчетах в десятичной дроби;
2) индекс инфляции (J i) в рассматриваемом периоде (n), определяемый как 1 + Т i.

Корректировка наращенной стоимости денежных средств с учетом инфляции осуществляется по формуле:

где K р — будущая реальная стоимость денежных средств;
K н — будущая номинальная стоимость денежных средств;
J i — прогнозируемый индекс инфляции.

Расчеты, проведенные по этой формуле, позволяют определить реальную будущую стоимость денежных средств, если в процессе ее наращения в используемой ставке процента не была учтена ее инфляционная составляющая.