
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Б. Оптимальная комбинация факторов производстваСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Соединим теперь изокосту и карту изоквант (тема 6, п. 1) на одной диаграмме (рис. 7-3): Рис. 7-3. Экономически эффективный выпуск
На рисунке помещены три изокванты и одна изокоста. Напомним, что изокванта отражает все комбинации труда и капитала, при которых выпуск остается неизменным. При этом изокванта, расположенная выше и правее предыдущей, соответствует большему объему выпуска. Объемы выпуска (q1, q2, q3) приведены рядом с соответствующей изоквантой. В свою очередь, изокоста отражает все комбинации труда и капитала, доступные фирме при данных совокупных затратах и ценах труда и капитала. Отсюда вытекает, что в т. А, В и С выпуск одинаков, ибо все они находятся на одной изокванте. При этом совокупные затраты в т. А и С тоже равны, поскольку эти точки принадлежат одной изокосте. В т. В затраты ниже, т.к. она предполагает использование меньшего количества труда и капитала, т.е. принадлежит более «низкой» изокосте, не изображенной на рисунке. Нас, однако, интересует, какой максимальный выпуск достижим при заданных совокупных затратах. Искомый выпуск – q2 – определяется точкой касания изокосты и самой высокой из доступных изоквант (т. Е). Для его достижения фирма должна использовать Итак, применяя Напомним, что все точки на любой изокванте (например, на изокванте q2) отражают различные технически эффективные способы производства данного объема продукции (тема 6, п. 1). Но только в т. Е выпуск q2 получается с минимально возможными затратами. Таким образом, комбинация Вспомним также, что в любой точке на изокванте предельная норма технической замены капитала трудом равна отношению предельных продуктов труда и капитала, т.е. выполняется равенство (тема 6, п. 2):
В то же время, в точке оптимальной комбинации факторов производства предельная норма технической замены равняется еще и отношению цен труда и капитала. Иными словами, указанное равенство принимает вид:
Обосновать это можно так. Пусть в некоторой точке на изокванте предельный продукт труда составляет 10 единиц определенного продукта, а предельный продукт капитала равен 5 единицам. Отношение предельных продуктов равно, следовательно, 2:1. При этом цены труда и капитала, допустим, равны, т.е. соотношение цен составляет 1:1. Таким образом, имеет место неравенство:
В результате, отказываясь от одной единицы капитала, фирма теряет 5 единиц выпуска. Однако на сэкономленные деньги она может нанять еще одну единицу труда, что принесет ей дополнительно 10 единиц выпуска. В таких условиях, заменяя капитал трудом, фирма увеличивает свой выпуск при неизменных затратах, т.е. переходит на более высокую изокванту, оставаясь на той же изокосте. Фирма будет, следовательно, заменять капитал трудом до тех пор, пока не достигнет точки оптимальной комбинации факторов, которой соотношения предельных продуктов и цен труда и капитала не сравняются друг с другом.[1] Теперь представим, что фирма оказалась в той точке на изокванте, где отношение предельных продуктов труда и капитала меньше соотношения их цен. В этом случае, ей становится выгодно заменять труд капиталом, опять-таки вплоть до достижения точки оптимальной комбинации факторов. Пойдем дальше. Пусть оптимальная комбинация труда и капитала достигнута. Если фирма увеличивает свои затраты, изокоста смещается вправо – вверх. Соответственно точками оптимума последовательно становятся E1, E2, E3 на все более высоких изоквантах. Соединив эти точки, получаем линию «путь развития» (рис. 7-4). Рис 7-4. Линия «путь развития»
Изменение наклона этой линии говорит о том, использование какого фактора относительно возрастает при увеличении производства. В. Математическое приложение Пусть производственная функция выглядит так (тема 6, п. 1): q=AKaLb Параметры А, α и β нам известны. Известна также функция совокупных затрат – изокоста: TC=PK*K+PL*L Фирме надо определить оптимальную комбинацию труда и капитала, позволяющую достичь максимального выпуска при заданных совокупных затратах и ценах труда и капитала. Выше было приведено графическое решение этой задачи: наилучшая комбинация факторов производства соответствует точке касания заданной изокосты и самой высокой из доступных изоквант. Теперь ту же задачу предстоит решить аналитически. Мы помним, что в точке оптимальной комбинации факторов соблюдается равенство:
Функции предельных продуктов труда и капитала можно получить, взяв производные производственной функции соответственно по труду и по капиталу (тема 6, п. 2):
Таким образом:
Следовательно:
Вспоминаем о функции совокупных затрат и получаем систему из двух уравнений с двумя неизвестными (L и K): TC=PK*K+PL*L и Решая эту систему, находим оптимальные величины труда и капитала:
Виды затрат В предыдущем параграфе в поисках оптимальной комбинации факторов производства фирма могла изменять как труд, так и капитал. Однако на практике фирме значительно легче нанять дополнительных работников, нежели приобрести новое оборудование – капитал. Последнее требует большего времени. В связи с этим в теории производства различают короткий и длительный периоды. В длительном периоде для увеличения выпуска фирма может изменить все факторы производства. В коротком периоде одни факторы производства являются переменными, а другие – постоянными. Здесь для увеличения выпуска фирма может измерить лишь переменные факторы. Цены на факторы производства в коротком периоде полагаются фиксированными. Отсюда вытекает, что все затраты фирмы в коротком периоде можно разделить на постоянные и переменные. Постоянные затраты (FC) – это затраты, величина которых не меняется вместе с изменением объема выпуска, т.е. это затраты постоянных факторов производства. Обычно постоянными затратами являются амортизация, арендная плата, процент за кредит, заработная плата руководства и конторских служащих и т.д. К постоянным, как правило, относятся и неявные затраты. Переменные затраты (VC) – это затраты, величина которых меняется вместе с изменением объема выпуска, т.е. это затраты переменных факторов производства. К ним обычно относятся заработная плата производственных рабочих, расходы на сырье и материалы, электроэнергию для технологических целей и т.д. В теоретических микроэкономических моделях к переменным затратам обычно относят расходы на оплату труда, а к постоянным затратам – расходы на оплату капитала. С этой точки зрения величина переменных затрат равна произведению цены одного человеко-часа труда (PL) на количество человеко-часов (L): VC=PL*L В свою очередь, величина постоянных затрат равна произведению цены одного машино-часа капитала (PK) на количество машино-часов (K): FC=Pk*K Сумма постоянных и переменных затрат дает нам совокупные затраты (TC): FC+VC=TC Помимо совокупных затрат необходимо знать и средние затраты. Средние постоянные затраты (AFC) – это постоянные затраты, приходящиеся на единицу выпуска:
Средние переменные затраты (AVC) – это переменные затраты, приходящиеся на единицу выпуска:
Средние совокупные затраты (AC) – это совокупные затраты, приходящиеся на единицу выпуска или сумма средних постоянных и средних переменных затрат:
При анализе рыночного поведения фирмы большую роль играют предельные затраты. Предельные затраты (MC) отражают прирост совокупных затрат при увеличении выпуска (q) на одну единицу:
Поскольку с ростом выпуска возрастают лишь переменные затраты, приращение совокупных затрат равно приращению переменных затрат (DTC=DVC). Можно, следовательно, записать:
Можно сказать и так: предельные затраты – это затраты, связанные с выпуском последней единицы продукции. Приведем пример расчета затрат. Пусть при выпуске 10 ед. переменные затраты составляют 100, а при выпуске 11 ед. они достигают 105. Постоянные затраты не зависят от выпуска и равны 50. Тогда:
В нашем примере выпуск увеличился на 1 ед. (Dq=1), при этом переменные и суммарные затраты возросли на 5 (DVC=DTC=5). Следовательно, дополнительная единица выпуска потребовала увеличения затрат на 5. Это и есть предельные затраты производства одиннадцатой единицы продукции (МС=5). Если функция совокупных (переменных) затрат непрерывна и дифференцируема, то определить предельные затраты для заданного объема выпуска можно, взяв производную этой функции по выпуску:
Затраты в коротком периоде
|
||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-12; просмотров: 914; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.223.171.83 (0.009 с.) |


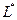 труда и
труда и  капитала. При всех иных доступных фирме комбинациях факторов производства выпуск будет меньше, поскольку в этих случаях фирма окажется на более «низких» изоквантах. В то же время более «высокие» изокванты – например изокванта q3 – расположены выше изокосты, а, значит, недоступны фирме при данных совокупных затратах и ценах труда и капитала.
капитала. При всех иных доступных фирме комбинациях факторов производства выпуск будет меньше, поскольку в этих случаях фирма окажется на более «низких» изоквантах. В то же время более «высокие» изокванты – например изокванта q3 – расположены выше изокосты, а, значит, недоступны фирме при данных совокупных затратах и ценах труда и капитала.
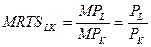
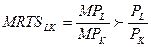
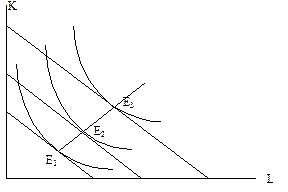
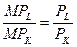
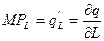 и
и 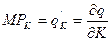
 и
и 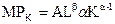

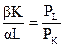
 и
и 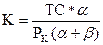
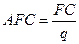




 или
или 



