
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производственный выбор в долгосрочном периодеСодержание книги
Поиск на нашем сайте Производственная функция в долгосрочном периоде состоит в определении оптимальных комбинации факторов и размеров производства, которые обеспечивали бы максимальный объем выпуска. Ограничимся рассмотрением двух факторов производства: труда (L) – переменный фактор и капитала (K) – постоянный фактор. Это позволит максимально упростить анализ и в то же время выявить основные закономерности процесса производства. Отчасти это допущение соответствует реальности, так как такие элементы капитала как производственные здания и сооружения, сложное оборудование невозможно увеличить за сравнительно короткое время (в отличии, например, от найма дополнительных работников). В условиях заданных предпосылок производственная функция принимает вид: Q = F (L, K). При этом труд и капитал измеряются обычно в единицах потока, например, в единицах времени (часах) использования, соответственно, труда и капитала. Используя одинаковое количество факторов производства, разные фирмы могут получать разные количества продукции в зависимости от уровня организации производства. Производственная функция не учитывает особенностей в организации труда и производства на отдельных предприятиях. Сочетание ресурсов, которое необходимо для получения какого-либо выпуска, характеризует определенный способ производства. Различные способы производства могут быть представлены в виде производственной сетки, являющейся табличной формой выражения производственной функции. Таблица 7.1. Производственная сетка (Q=F(L,K))
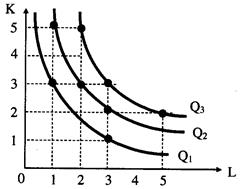
Производственная сетка показывает, что один и тот же объем выпуска может быть произведен при разных комбинациях факторов производства. Например, Q = 65 может быть произведен при комбинации факторов 3K;1L и при комбинации 1K;3L. Эту взаимосвязь можно представить графически (рис. 7.3). Изокванта – кривая, демонстрирующая различные варианты комбинаций факторов производства, которые могут быть использованы для выпуска данного объема продукта. Изокванты иначе называют кривыми равных продуктов, или линиями равного выпуска. Чем дальше от начала координат расположена изокванта, тем больший объем выпуска она представляет. Карта изоквант, представляющая собой набор возможных изоквант, показывает все допустимые варианты осуществления производства.
Рис.7.3. Карта изоквант
Изокванты строятся на основе эмпирических данных, полученных на основе анализа конкретного производственного процесса, поэтому они несут в себе определенные характеристики этого производства. Наклон изокванты выражает зависимость одного фактора от другого в производственном процессе, при этом увеличение одного фактора и уменьшение другого не вызывают изменений в объеме выпускаемой продукции. Положительный наклон изокванты означает, что увеличение применения одного фактора потребует увеличения применения другого фактора, чтобы не сократить выпуск продукции. Отрицательный наклон изокванты показывает, что сокращение одного фактора (при определенном объеме производства) всегда будет вызывать увеличение другого фактора. Крутизна наклона изокванты выражает предельную норму технологического замещения (MRTS), которая измеряется соотношением изменения объема выпуска продукции. Предельная норма технологического замещения трудом капитала (MRTSLK) определяется величиной капитала, которую может заменить каждая единица труда, не вызывая изменения объема выпуска продукции. Предельная норма технического замещения в любой точке изокванты равна наклону касательной в этой точке, умноженному на -1:
Поскольку замещение факторов предполагает сохранение объема выпуска, то предельная норма технологического замещения оказывается тесно связанной с предельными продуктами факторов производства. Увеличение труда (ΔL) означает рост объема выпуска на MPL×ΔL. Чтобы остаться на той же изокванте, необходимо компенсировать это увеличение за счет сокращения применения капитала на величину ΔK, которая даст сокращение выпуска на MPK×ΔK. Следовательно, чтобы выпуск оставался неизменным должно выполняться равенство (MPL×ΔL) + (MPK×ΔK) = 0, или MPL×ΔL = -MPK×ΔK. Таким образом, В долгосрочном периоде фирма имеет возможность не только комбинировать факторы производства, но и изменять их количество. В этом случае говорят об изменении размера или масштаба производства. Эффект масштаба – это свойство производственного процесса, отражающее характер изменения соотношения между увеличением затрат факторов производства и изменением объема выпуска. Предположим, что фирма увеличивает использование всех факторов производства в одинаковой пропорции, например в n раз. Если производственная функция задана выражением Q = F (L, K), то все ресурсы умножаются на одну и ту же положительную величину n >1. Это означает, что изменился масштаб производства, который приведет к росту выпуска. В зависимости от характера изменения соотношения между увеличением факторов и ростом выпуска возможны следующие ситуации:
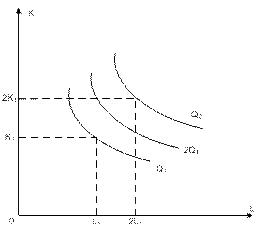
Рис.7.4. Постоянный эффект масштаба · выпуск возрастает в n раз – неизменная отдача от масштаба (рис.7.4), F (nL, nK) = nF (L, K); Постоянный эффект масштаба выражается в том, что объем выпуска изменяется в той же пропорции, что и затраты факторов. · выпуск возрастает меньше, чем в n раз – возрастающая отдача от масштаба (рис.7.5), F (nL, nK) < nF (L, K);
Рис.7.5. Положительный (возрастающий) эффект масштаба Положительный эффект масштаба выражается в том, что объем выпуска увеличивается в большей пропорции, чем затраты факторов. · выпуск возрастает больше чем в n раз – убывающая отдача от масштаба (рис.7.4), F (nL, nK) > nF (L, K);
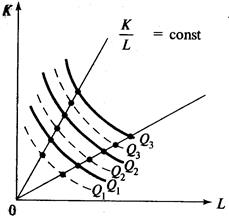
Рис.7.6. Отрицательный (убывающий) эффект масштаба Отрицательный эффект масштаба выражается в том, что объем выпуска увеличивается в меньшей пропорции, чем затраты факторов. Определение эффекта масштаба может быть дано, например, через понятие производительности труда, которая измеряется показателем среднего продукта труда. Если увеличение масштаба производства не приводит к изменению производительности труда, это говорит о неизменном эффекте масштаба. Убывающий эффект масштаба сопровождается снижением производительности труда, возрастающий – ее повышением. Поскольку характер и длительность действия эффекта масштаба обусловлены особенностями технологии, то для каждой отрасли будет характерен свой оптимальный масштаб производства – тот, при котором краткое увеличение факторов не приводит к снижению эффективности производстваё. Кроме того, развитие технологий позволяет осуществлять производство того же продукта с меньшими издержками. В этом смысле технический прогресс становится фактором роста производства и его влияние проявляется двояко: увеличением объема выпуска при данном количестве факторов производства и снижением их затрат. Воздействие технического прогресса в долгосрочном периоде выражается в смещении изокванты и изменении ее конфигурации (рис. 7.7, 7.8, 7.9). Сплошные изокванты характеризуют производство до нововведений. Сдвиг изоквант в положение пунктирных линий характеризует влияние технического прогресса. Различают три типа технического прогресса: нейтральный, капиталоинтенсивный (трудосберегающий), трудоинтенсивный (капиталосберегающий). Нейтральный тип технического прогресса характеризуется изменениями в технологии, которые в равной степени способствуют повышению производительности и труда, и капитала, так что предельная норма технологического замещения сохраняется постоянной. При этом не меняется наклон изокванты, она перемещается параллельно самой себе (рис. 7.7).
Рис.7.7. Нейтральный тип технического прогресса
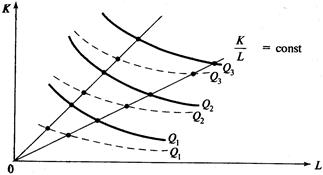
Трудоинтенсивный тип технического прогресса характеризуется изменениями в технологии, которые способствуют повышению производительности труда, т.е. при неизменном соотношении затрат труда и капитала MRTSLK повышается. Изокванты, сдвигаясь к началу координат, становятся круче (рис. 7.8).
Рис.7.8. Трудоинтенсивный тип технического прогресса
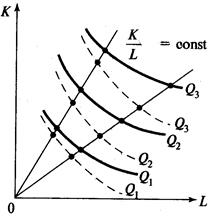
Капиталоинтенсивный тип технического прогресса характеризуется изменениями в технологии, которые способствуют повышению предельной производительности капитала, т.е. при неизменном соотношении затрат труда и капитала MRTSLK снижается. Изокванты не только сдвигаются к началу координат, но становятся более пологими во всех точках, лежащих на одних и тех же лучах, проведенных из начала координат, где соотношение труда и капитала неизменно (рис. 7.9).
Рис.7.9. Капиталоинтенсивный тип технического прогресса
На практике технологические изменения, как правило, сопровождаются изменением количества используемых ресурсов. При этом важно определить, в какой степени рост выпуска связан с увеличением объема факторов производства и в какой мере он является результатом технического прогресса.
|
|||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 370; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.41 (0.008 с.) |

 Если исходить из двухфакторной модели производства и откладывать применяемые количества факторов производства в горизонтальной плоскости по осям K и L, то по вертикальной плоскости можно зафиксировать значения объема выпуска для каждой комбинации факторов. Каждый конкретный уровень выпуска будет зависеть от изменения величин обоих факторов производства. Для каждого типа комбинации факторов изменения объемов выпуска графически будут выражаться в форме дуг. Если производственная функция является непрерывной, то все достижимые объемы выпуска при всех комбинациях факторов производства будут представлены в виде поверхности, по форме напоминающей холм, называемый экономистами «холмом производства».
Если исходить из двухфакторной модели производства и откладывать применяемые количества факторов производства в горизонтальной плоскости по осям K и L, то по вертикальной плоскости можно зафиксировать значения объема выпуска для каждой комбинации факторов. Каждый конкретный уровень выпуска будет зависеть от изменения величин обоих факторов производства. Для каждого типа комбинации факторов изменения объемов выпуска графически будут выражаться в форме дуг. Если производственная функция является непрерывной, то все достижимые объемы выпуска при всех комбинациях факторов производства будут представлены в виде поверхности, по форме напоминающей холм, называемый экономистами «холмом производства».
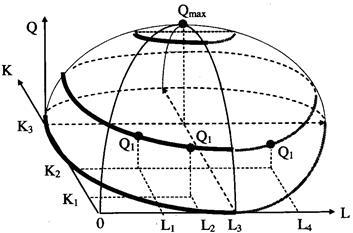 «Холм производства»
«Холм производства»
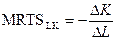 .
.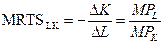 , т.е. предельная норма технологического замещения факторов производства равна обратному соотношению их предельных продуктов. Данное равенство говорит о том, что в любой точке изокванты предельная норма замещения одного ресурса другим равна наклону касательной к точке, лежащей на изокванте.
, т.е. предельная норма технологического замещения факторов производства равна обратному соотношению их предельных продуктов. Данное равенство говорит о том, что в любой точке изокванты предельная норма замещения одного ресурса другим равна наклону касательной к точке, лежащей на изокванте.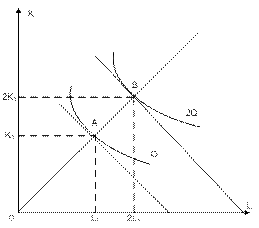
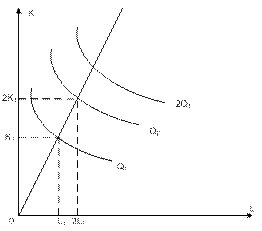
 где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда, a >, α > 0 – числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях.
Для многофакторного производства функция Кобба-Дугласа имеет вид:
где Y - объем выпуска, K - величина производственных фондов (капитал), L - затраты труда, a >, α > 0 – числовые параметры (масштабное число и показатель эластичности). Благодаря своей простоте и рациональности, эта функция широко применяется до сих пор и получила дальнейшие обобщения в различных направлениях.
Для многофакторного производства функция Кобба-Дугласа имеет вид:
 ,
,  Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса)
Для учета технического прогресса в функцию Кобба-Дугласа вводят специальный множитель (технического прогресса)  , где t - параметр времени, ν – постоянное число, характеризующее темп развития. В результате функция принимает «динамический» вид:
, где t - параметр времени, ν – постоянное число, характеризующее темп развития. В результате функция принимает «динамический» вид:  , где не обязательно α + β = 1. Показатели степени в функции имеют смысл эластичности выпуска по капиталу и труду.
, где не обязательно α + β = 1. Показатели степени в функции имеют смысл эластичности выпуска по капиталу и труду.



